卡尔曼滤波（Kalman Filtering）基础知识（方差、协方差与相关系数）

转载 已于 2023-09-25 20:49:07 修改 · 2.9k 阅读 · 7
文章标签：

#deep learning

于 2023-09-25 20:46:07 首次发布
本文详细解释了卡尔曼滤波中的关键概念，包括方差、协方差和相关系数，阐述了它们在衡量随机变量间关系和预测中的作用，以及如何通过公式理解这些统计量。

卡尔曼滤波（Kalman Filtering）——（2）基础知识（方差、协方差与相关系数）

背景

卡尔曼滤波预测中用到协方差，查了相关资料，以此记录。
在这里插入图片描述

协方差

协方差（Covariance）在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况，即当两个变量是相同的情况。
协方差表示的是两个变量的总体的误差，这与只表示一个变量误差的方差不同。如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值。如果两个变量的变化趋势相反，即其中一个大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。

协方差公式

在这里插入图片描述

一、 方差

方差是各个数据与平均数之差的平方的平均数。在概率论和数理统计中，方差（英文Variance）用来度量随机变量和其数学期望（即均值）之间的偏离程度。在许多实际问题中，研究随机变量和均值之间的偏离程度有着很重要的意义。
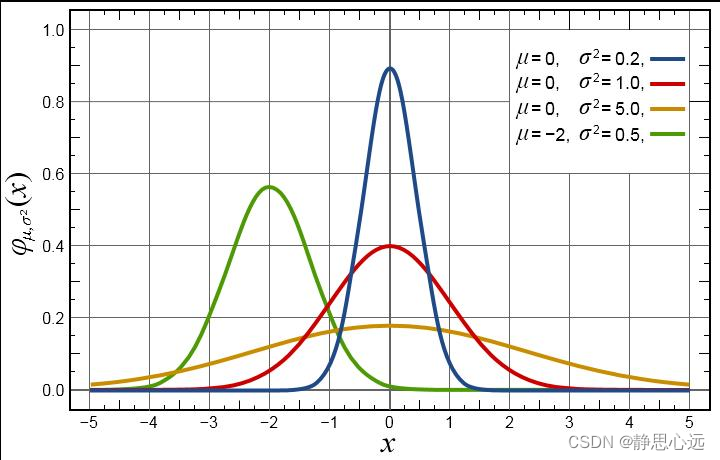
  在这里插入图片描述

二、标准差

方差开根号。

三、协方差

在概率论和统计学中，协方差用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况，即当两个变量是相同的情况。
在这里插入图片描述
 可以通俗的理解为：两个变量在变化过程中是否同向变化？还是反方向变化？同向或反向程度如何？

  • 你变大，同时我也变大，说明两个变量是同向变化的，这是协方差就是正的。
  • 你变大，同时我变小，说明两个变量是反向变化的，这时协方差就是负的。
  • 如果我是自然人，而你是太阳，那么两者没有相关关系，这时协方差是0。

从数值来看，协方差的数值越大，两个变量同向程度也就越大，反之亦然。
  可以看出来，协方差代表了两个变量之间的是否同时偏离均值，和偏离的方向是相同还是相反。
公式：如果有X,Y两个变量，每个时刻的“X值与其均值之差”乘以“Y值与其均值之差”得到一个乘积，再对这每时刻的乘积求和并求出均值，即为协方差。
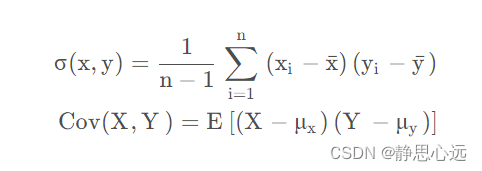
在这里插入图片描述
中间省略若干，数字基础太差。。。

  • 卡尔曼滤波（Kalman Filtering）——（2）基础知识（方差、协方差与相关系数）
    四、方差，标准差与协方差之间的联系与区别
  • 1.方差和标准差都是对一组(一维)数据进行统计的，反映的是一维数组的离散程度；而协方差是对2组数据进行统计的，反映的是2组数据之间的相关性。
  • 2.标准差和均值的量纲（单位）是一致的，在描述一个波动范围时标准差比方差更方便。比如一个班男生的平均身高是170cm,标准差是10cm,那么方差就是10cm^2。可以进行的比较简便的描述是本班男生身高分布是170±10cm，方差就无法做到这点。
  • 3.方差可以看成是协方差的一种特殊情况，即2组数据完全相同。
    协方差的计算公式为：
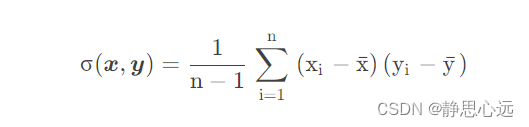
    在这里插入图片描述
    在这里插入图片描述
    4.协方差只表示线性相关的方向，取值正无穷到负无穷

四、相关系数

相关度的大小了：相关系数
协方差的相关系数，不仅表示线性相关的方向，还表示线性相关的程度，取值[-1,1]。也就是说，相关系数为正值，说明一个变量变大另一个变量也变大；取负值说明一个变量变大另一个变量变小，取0说明两个变量没有相关关系。同时，相关系数的绝对值越接近1，线性关系越显著。
相关系数：
1、也可以反映两个变量变化时是同向还是反向，如果同向变化就为正，反向变化就为负。
2、由于它是标准化后的协方差，因此更重要的特性来了：它消除了两个变量变化幅度的影响，而只是单纯反应两个变量每单位变化时的相似程度。
计算公式为：就是用X、Y的协方差除以X的标准差乘以Y的标准差。
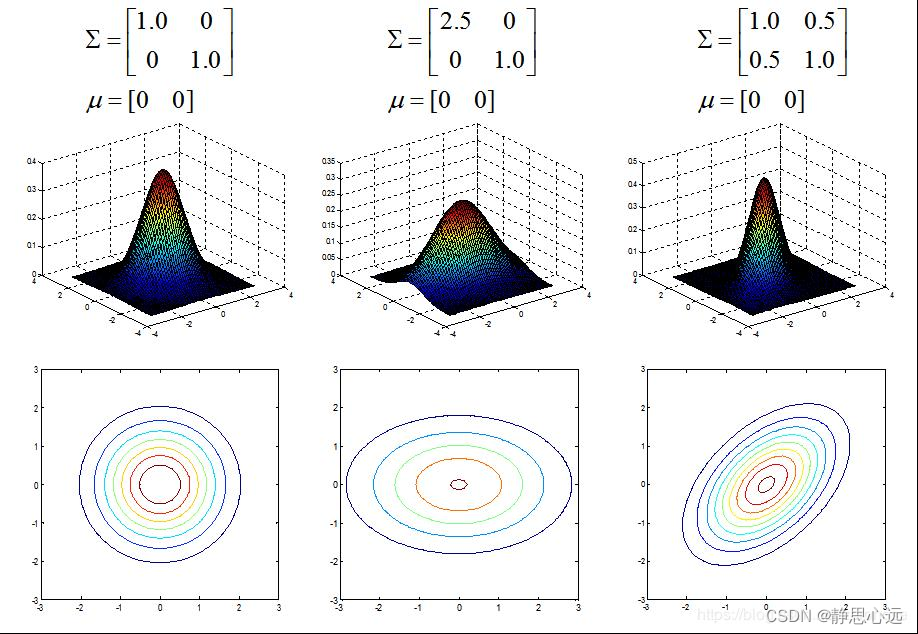
在这里插入图片描述
在概率论中，两个随机变量 X 与 Y 之间相互关系，大致有下列3种情况：
在这里插入图片描述

当 X, Y 的联合分布像左图那样时，我们可以看出，大致上有： X 越大 Y 也越大， X 越小 Y 也越小，这种情况，我们称为 “正相关”。

当X, Y 的联合分布像中图那样时，我们可以看出，大致上有：X 越大Y 反而越小，X 越小 Y 反而越大，这种情况，我们称为 “负相关”。

当X, Y 的联合分布像右图那样时，我们可以看出：既不是X 越大Y 也越大，也不是 X 越大 Y 反而越小，这种情况我们称为 “ 不相关”。

怎样将这3种相关情况，用一个简单的数字表达出来呢？

  • 在图中的区域（1）中，有 X>EX ，Y-EY>0 ，所以(X-EX)(Y-EY)>0；
  • 在图中的区域（2）中，有 X<EX ，Y-EY>0 ，所以(X-EX)(Y-EY)<0；
  • 在图中的区域（3）中，有 X<EX ，Y-EY<0 ，所以(X-EX)(Y-EY)>0；
  • 在图中的区域（4）中，有 X>EX ，Y-EY<0 ，所以(X-EX)(Y-EY)<0。

当X 与Y 正相关时，它们的分布大部分在区域（1）和（3）中，小部分在区域（2）和（4）中，所以平均来说，有E(X-EX)(Y-EY)>0 。

当 X与 Y负相关时，它们的分布大部分在区域（2）和（4）中，小部分在区域（1）和（3）中，所以平均来说，有(X-EX)(Y-EY)<0 。

当 X与 Y不相关时，它们在区域（1）和（3）中的分布，与在区域（2）和（4）中的分布几乎一样多，所以平均来说，有(X-EX)(Y-EY)=0 。
所以，我们可以定义一个表示X, Y 相互关系的数字特征，也就是协方差。

cov(X,Y)=E(X−EX)(Y−EY)

  • 当 cov(X, Y)>0时，表明 X与Y 正相关；
  • 当 cov(X, Y)<0时，表明X与Y负相关；
  • 当 cov(X, Y)=0时，表明X与Y不相关。

这就是协方差的意义。
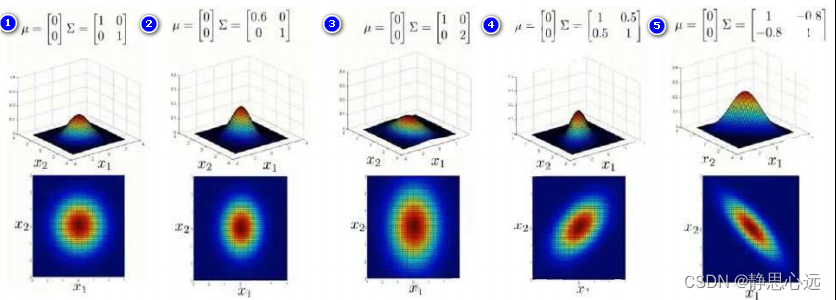
协方差矩阵的主对角线就是方差，反对角线上的就是两个变量间的协方差。
就上面的二元高斯分布而言，协方差越大，图像越扁，也就是说两个维度之间越有联系。

特别提示

上面的公式和数据并非我推导或者验证，仅做参考。

引用博客

图像处理之目标跟踪（一）之卡尔曼kalman滤波跟踪（主要为知识梳理）（转载）
coming_is_winter的博客
01-12 7万+
图像处理之目标跟踪(一)之卡尔曼kalman滤波跟踪(主要为知识梳理)(转载) 内容不是一篇文章的转载而是几篇内容的综合梳理. 主要来源： EmbeddedApp 运动目标跟踪（一）--搜索算法预测模型之KF,EKF,UKF（文献1，主要是原理的梳理，十分详细） -Sherma...
卡尔曼滤波器详解（二）：数学基础
@清欢_
07-30 2838
文章目录卡尔曼滤波器：数学基础一、数据融合1. 结论2. 推导二、协方差矩阵1. 定义方差协方差2. 公式三、状态空间表达 博客讨论三个方面：数据融合、协方差矩阵、状态空间方程和观测器。 卡尔曼滤波器：数学基础 一、数据融合   假设存在两次测量，两次测量均存在误差且误差服从正态分布。   第一次测量的测量值为z1z_1z1​，标准差为σ1\sigma_1σ1​；第二次测量的测量值为z2z_2z2​，标准差为σ2\sigma_2σ2​。 1. 结论   估计真实值在两次测量值之间，且更接近标准差小的测量
卡尔曼滤波（Kalman filtering）
最新发布
weixin_42260296的博客
09-27 924
卡尔曼滤波（KF）是一种利用系统状态方程和观测数据对系统状态进行最优估计的算法，通过加权测量值和预测值来减小噪声影响。其核心包括预测和更新两个步骤：预测阶段通过状态方程估计当前状态，更新阶段利用卡尔曼增益结合观测值修正估计。KF假设噪声服从高斯分布且相互独立。扩展卡尔曼滤波（EKF）将KF推广到非线性系统，通过局部线性化（雅可比矩阵）处理非线性问题，但存在计算复杂和强非线性下性能下降的局限性。KF/EKF广泛应用于导航、控制等领域的状态估计问题。
卡尔曼滤波（Kalman Filtering）——（2）基础知识（方差、协方差与相关系数）
曾记否@
08-08 6661
卡尔曼滤波----方差、协方差与相关系数正态分布（高斯分布）标准差协方差方差，标准差与协方差之间的联系与区别相关系数参考文献 正态分布（高斯分布）   正态分布是一种概率分布。正态分布是具有两个参数μ和σ2的连续型随机变量的分布，第一参数μ是遵从正态分布的随机变量的均值，第二个参数σ2是此随机变量的方差，所以正态分布记作N(μ，σ2 )。遵从正态分布的随机变量的概率规律为取 μ邻近的值的概率大 ，而取离μ越远的值的概率越小；σ越小，分布越集中在μ附近，σ越大，分布越分散。正态分布的密度函数的特点是：关于μ对
卡尔曼滤波-卡尔曼滤波基础知识（均值、方差、标准差、协方差、相关系数与协方差矩阵）
永远的我们的博客
08-09 1673
卡尔曼滤波基础知识（均值、方差、标准差、协方差、相关系数与协方差矩阵）
卡尔曼滤波简介——4.方差比较
weixin_34106122的博客
04-24 660
最下面的分布是一个相对不确定的分布，我们对之所知甚少 转载于:https://www.cnblogs.com/fuhang/p/8932581.html
卡尔曼滤波的数学基础
3D视觉工坊
08-30 218
来源：FunIO卡尔曼滤波是一种用于估算线性动态系统状态的优化算法，其基础数学理论为贝叶斯定理，将传感器测量值和系统模型的预测值进行融合，得到对系统状态的估计。贝叶斯定理是基于条件概率的公式，用于计算给定某些证据的情况下，事件发生的概率。在卡尔曼滤波中，贝叶斯定理用于估算系统状态的后验概率分布，即给定过去和当前的观测值，预测未来状态的概率分布。以下是卡尔曼滤波的数学基础：状态空间模型卡尔曼滤波的核...
滤波笔记一：卡尔曼滤波（Kalman Filtering）详解
热门推荐
scoutee的博客
07-02 13万+
卡尔曼滤波法的详解，包括公式推导，算法迭代步骤以及python源代码。
详解卡尔曼滤波（Kalman Filter）
weixin_55252589的博客
12-30 5124
黑盒（Black Box）思想最早由维纳（Wiener）在1939年提出，即假定我们对从数据到估计中间的映射过程一无所知，仅仅用线性估计（我们知道在高斯背景下，线性估计能达到克拉美劳下界，是最优估计）来掩盖我们的无知。但是，到了二十年以后的1960年卡尔曼的年代，我们对于红框内的事（prior knowledge），很有可能是知道的，并且知道得很详细，很清楚。再这样的情况下，我们还不能有效地利用这一部分先验知识来帮助我们把估计做的更好就没有任何道理了。卡尔曼就是从红框入手，将这部分先验信息表达出来。至于怎么
Kalman算法、扩展卡尔曼滤波（EKF）和无迹卡尔曼滤波（UKF）的比较
zhulong1984的博客
09-21 2572
计算复杂度：EKF通常计算复杂度较低，而UKF计算复杂度较高。处理非线性能力：UKF在处理高度非线性系统时表现更好，精度更高；EKF在非线性程度不高的系统中也能有效工作。实现复杂度：EKF需要计算雅可比矩阵，这在某些情况下较复杂；UKF不需要计算雅可比矩阵，但需要生成和处理sigma点，逻辑上更复杂。
卡尔曼滤波（Kalman filtering）——通俗易懂版本
漫长IT路
08-18 2050
文章目录引入 引入   首先请大家思考个问题，假设你手头有两个传感器A和B，测的是同一个信号。可是由于测量误差的原因它们每次的读数都不太一样，怎样才能获取到更准确的数据？ 取平均 简单粗暴，直接将两个传感器获得的数据求平均值：(A+B)/2(A+B)/2(A+B)/2，good。 加权平均 假设传感器A精度比传感器B高，那么就可以就可以使用加权平均来计算：A∗ω+B∗(1−ω),ω∈(0.5,1)A*\omega+B*(1-\omega), \omega \in(0.5,1)A∗ω+B∗(1−ω),ω∈(
通过简单直观的推导理解卡尔曼滤波器的基础（英文版）
04-17
本文提供了卡尔曼滤波器的简单直观推导，旨在为不需要强大数学背景的学科的学生讲授这个有用的工具。理解这种推导所需的最复杂的数学水平是将两个高斯函数相乘并将结果简化为紧凑形式的能力。
Kalman Filtering
09-06
Originally developed for use in spacecraft navigation, the Kalman filter turns out to be useful for many applications. It is mainly used to estimate system states that can only be observed indirectly or inaccurately by the system itself.
kalman filtering
08-01
关于kalman filtering的国外经典教材
kalman filtering in R(R语言实现卡尔曼滤波）
07-13
卡尔曼滤波（平方根算法、序贯算法、线性卡尔曼滤波、扩展卡尔曼滤波、区间卡尔曼滤波、系统误差和观测误差有关的卡尔曼滤波）在R语言中的实现，详细讲述了原理和其中工具包的使用，英文原版。
卡尔曼滤波 | Matlab实现卡尔曼滤波(Kalman Filtering)设计稳态滤波器和时变卡尔曼滤波器
算法如诗的博客
02-12 999
卡尔曼滤波 | Matlab实现卡尔曼滤波(Kalman Filtering)设计稳态滤波器和时变卡尔曼滤波器
卡尔曼滤波(Kalman Filter)状态估计、协方差矩阵、数据融合，看这一文即可，【非常详细推导，认真推理，包你看得懂】 上
weixin_47932058的博客
03-26 6231
卡尔曼滤波(Kalman Filter)状态估计、协方差矩阵、数据融合，看这一文即可，【非常详细推导，认真推理，包你看得懂】
卡尔曼滤波（2） 数学基础
GCUzxy666的博客
05-09 827
本节课我们要学习的是 卡尔曼滤波器的数学基础，数据融合，协方差矩阵，状态空间方程，观测器问题 一。数据融合（Data Fusion ) （一） 1.举例子：两个秤去称一个东西，分别有两个不一样的结果 2。数据：这两个标准差（Standard Deviation)都符合正态分布（也叫高斯分布） 3. 下面进行正态分布 这个在28~32g之间的概率是68.4% 4.预计结果： ...
卡尔曼滤波已知位置与CW方差估计加速度
03-03
### 卡尔曼滤波用于加速度方差估计 在卡尔曼滤波框架内，当已知位置数据时，可以通过扩展状态向量来估算加速度及其不确定性。具体而言，假设系统的状态由位置 \(p\)、速度 \(v\) 和加速度 \(a\) 组成，则状态转移模型可以表示为： \[ \begin{bmatrix} p_{k+1}\\ v_{k+1}\\ a_{k+1} \end{bmatrix}= \begin{bmatrix} 1 & T_s & \frac{T_s^2}{2}\\ 0 & 1 & T_s\\ 0 & 0 & 1 \end{bmatrix}\cdot\begin{bmatrix} p_k \\ v_k \\ a_k \end{bmatrix}+\begin{bmatrix} w_p \\ w_v \\ w_a \end{bmatrix}, \] 其中 \(T_s\) 是采样周期，\(w_p, w_v, w_a\) 表示过程噪声[^1]。 为了从观测到的位置信息中推断出加速度的方差，需要定义一个合适的观测矩阵 \(H\) 将实际测量的位置映射回状态空间: \[ z_k= H\cdot x_k+v_k=\begin{bmatrix} 1&0&0 \end{bmatrix}\cdot\begin{bmatrix} p_k \\ v_k \\ a_k \end{bmatrix}+v_k,\] 这里只考虑了位置作为直接可观测变量，而忽略了速度和加速度的直接测量[^4]。 接下来，初始化先验概率分布，即给定初始状态下各个参数均值与协方差矩阵 P 的设定。由于关注点在于计算加速度的不确定度（即方差），因此特别注意协方差矩阵右下角元素——它代表了对加速度估计的信心程度。随着每次迭代更新，此值会逐渐收敛至较为稳定的状态，反映出系统对于加速度认知的确信水平变化情况。 ```python import numpy as np def kalman_filter_update(x_pred, P_pred, z_measured, R, Q): """ Perform one step of Kalman Filter update. :param x_pred: Predicted state vector [px; vx; ax] :param P_pred: Prediction error covariance matrix :param z_measured: Measured position value :param R: Measurement noise covariance :param Q: Process noise covariance :return: Updated state estimate and updated error covariance """ # Observation model (only observing position) H = np.array([[1., 0., 0.]]) # Innovation or measurement residual y = z_measured - np.dot(H, x_pred) # Innovation (or residual) covariance S = np.dot(np.dot(H, P_pred), H.T) + R # Optimal Kalman gain K = np.dot(P_pred @ H.T, np.linalg.inv(S)) # Update the state with measurements x_estimated = x_pred + np.dot(K, y).reshape(-1, 1) # Update the estimation error covariance I = np.eye(len(x_pred)) P_updated = np.dot((I - np.dot(K, H)), P_pred) return x_estimated, P_updated # Example usage: Ts = 1.0 # Sampling time interval Q = np.diag([0.1, 0.1, 0.1]) ** 2 # Process noise covariance R = 5.0 ** 2 # Measurement noise variance # Initial estimates for position, velocity, acceleration initial_state_mean = np.zeros((3, 1)) P_initial = np.diag([1000, 1000, 1000]) # Simulated measured positions over time... measured_positions = [...] for pos in measured_positions: initial_state_mean, P_initial = kalman_filter_update( initial_state_mean, P_initial, pos, R=R, Q=Q ) print(f"Estimated Acceleration Variance after filtering: {P_initial[-1,-1]}") ``` 上述代码展示了如何基于一系列位置测量执行卡尔曼滤波算法，并最终输出经过多次迭代后的加速度方差估计结果。需要注意的是，这里的 `measured_positions` 应替换为真实应用场景下的连续位置读数序列[^2]。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值