Python代码实现PID控制

PID控制常用的简单分为位置式和增量式。

位置式PID

是输入的是目标位置到实际位置的偏差，输出的是(电机的)目标速度。

增量式PID控制.

数字PID控制算法的一种基本形式，是通过对控制量的增量（本次控制量和上次控制量的差值）进行PID控制的一种控制算法。
增量式PID控制

1、位置式

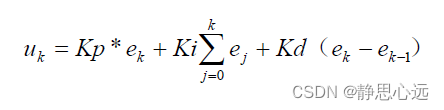
别的不说附上源代码，我用的是Python3，前提你得装上matplotlib这个库，这个库可以非常清楚的绘制数据的曲线图。如果不装的话可以返回一个列表

import matplotlib.pyplot as plt


class Pid():
	"""这里定义了一个关于PID的类"""
    def __init__(self, exp_val, kp, ki, kd):
        self.KP = kp
        self.KI = ki
        self.KD = kd
        self.exp_val = exp_val
        self.now_val = 0
        self.sum_err = 0
        self.now_err = 0
        self.last_err = 0

    def cmd_pid(self):
        self.last_err = self.now_err
        self.now_err = self.exp_val - self.now_val
        self.sum_err += self.now_err
        # 这一块是严格按照公式来写的
        self.now_val = self.KP * (self.exp_val - self.now_val) \
                        + self.KI * self.sum_err + self.KD * (self.now_err - self.last_err)
        return self.now_val


pid_val = []
#对pid进行初始化，目标值是1000 ，p=0.1 ，i=0.15, d=0.1
my_Pid = Pid(1000, 0.1, 0.15, 0.1)
# 然后循环100次把数存进数组中去
for i in range(0, 100):
    pid_val.append(my_Pid.cmd_pid())
plt.plot(pid_val)
plt.show()

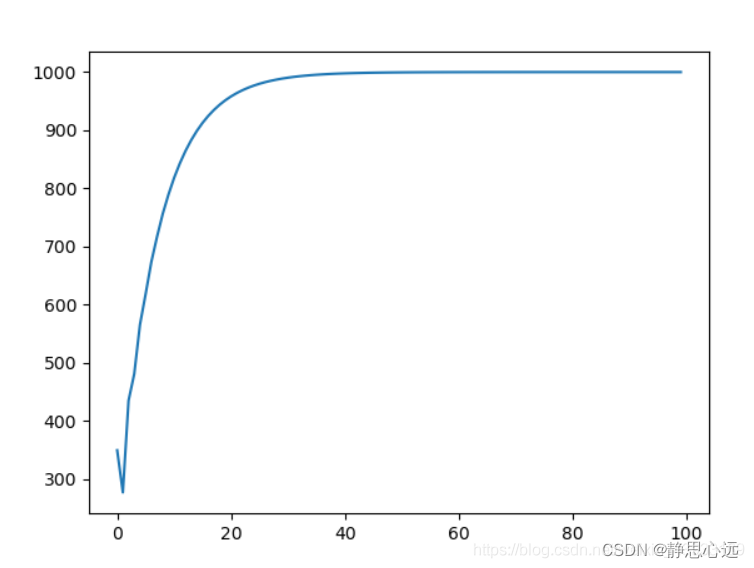
数据图

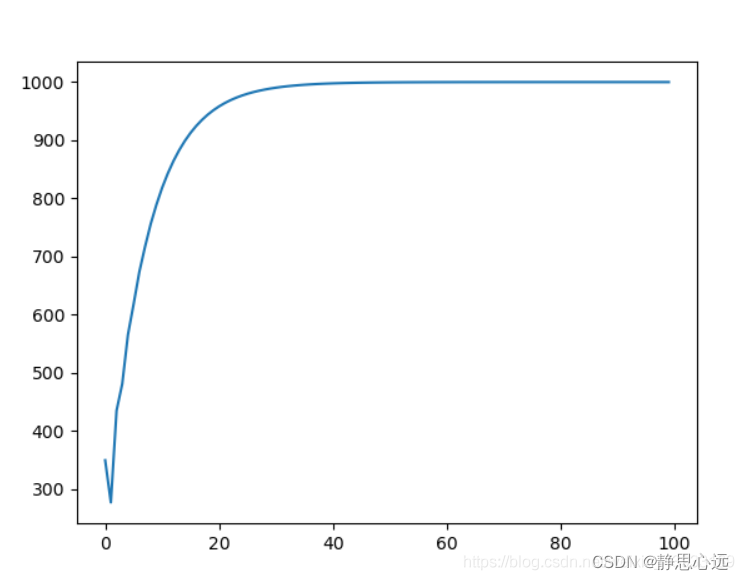
开始处有一个数据不对，把pd从0.1调小为0.01

import matplotlib.pyplot as plt


class Pid():
	#这里定义了一个关于PID的类
    def __init__(self, exp_val, kp, ki, kd):
        self.KP = kp
        self.KI = ki
        self.KD = kd
        self.exp_val = exp_val
        self.now_val = 0
        self.sum_err = 0
        self.now_err = 0
        self.last_err = 0

    def cmd_pid(self):
        self.last_err = self.now_err
        self.now_err = self.exp_val - self.now_val
        self.sum_err += self.now_err
        # 这一块是严格按照公式来写的
        self.now_val = self.KP * (self.exp_val - self.now_val) \
                        + self.KI * self.sum_err + self.KD * (self.now_err - self.last_err)
        return self.now_val


pid_val = []
#对pid进行初始化，目标值是1000 ，p=0.1 ，i=0.15, d=0.1
my_Pid = Pid(1000, 0.1, 0.15, 0.01)
# 然后循环100次把数存进数组中去
for i in range(0, 100):
    pid_val.append(my_Pid.cmd_pid())
plt.plot(pid_val)
plt.show()

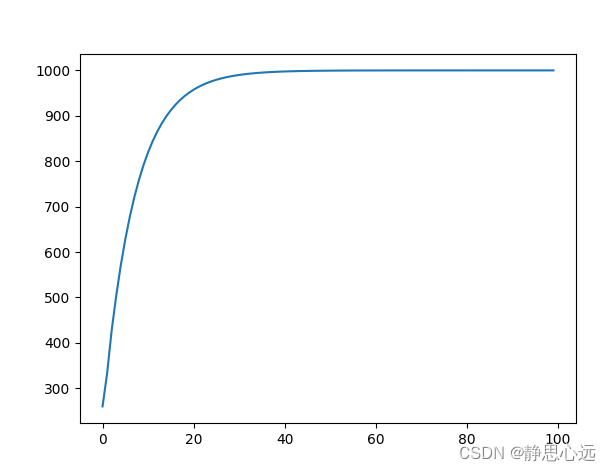
2、增量式

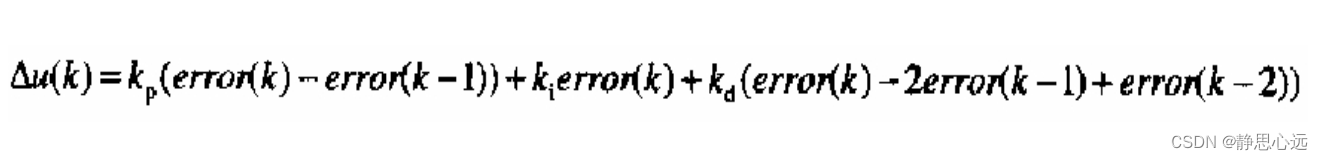
这就是离散化 PID 的增量式表示方式，由公式可以看出，增量式的表达结果和最
近三次的偏差有关，这样就大大提高了系统的稳定性。需要注意的是最终的输出
结果应该为 u(K)+增量调节值;

import matplotlib.pyplot as plt


class Pid():
    def __init__(self, exp_val, kp, ki, kd):
        self.KP = kp
        self.KI = ki
        self.KD = kd
        self.exp_val = exp_val
        self.now_val = 0
        self.now_err = 0
        self.last_err = 0
        self.last_last_err = 0
        self.change_val = 0

    def cmd_pid(self):
        self.last_last_err = self.last_err
        self.last_err = self.now_err
        self.now_err = self.exp_val - self.now_val
        self.change_val = self.KP * (self.now_err - self.last_err) + self.KI * \
            self.now_err + self.KD * (self.now_err - 2 * self.last_err
                                      + self.last_last_err)
        self.now_val += self.change_val
        return self.now_val


pid_val = []
my_Pid = Pid(1000000, 0.1, 0.15, 0.1)
for i in range(0, 30):
    pid_val.append(my_Pid.cmd_pid())
plt.plot(pid_val)
plt.show()

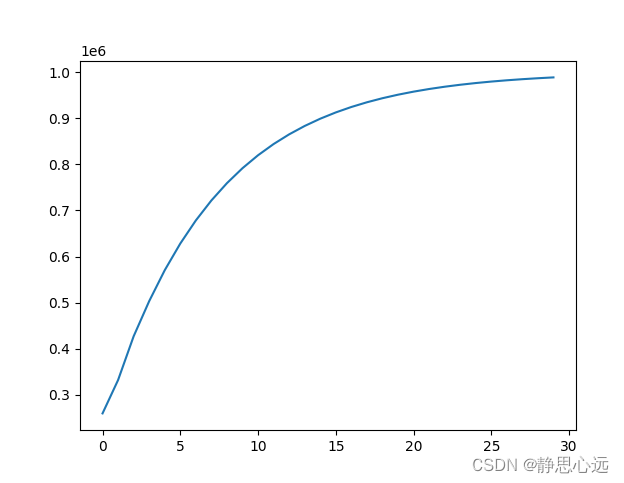
开始处有一个数据不对，把pd从0.1调小为0.01
my_Pid = Pid(1000000, 0.1, 0.15, 0.01)

3、口诀

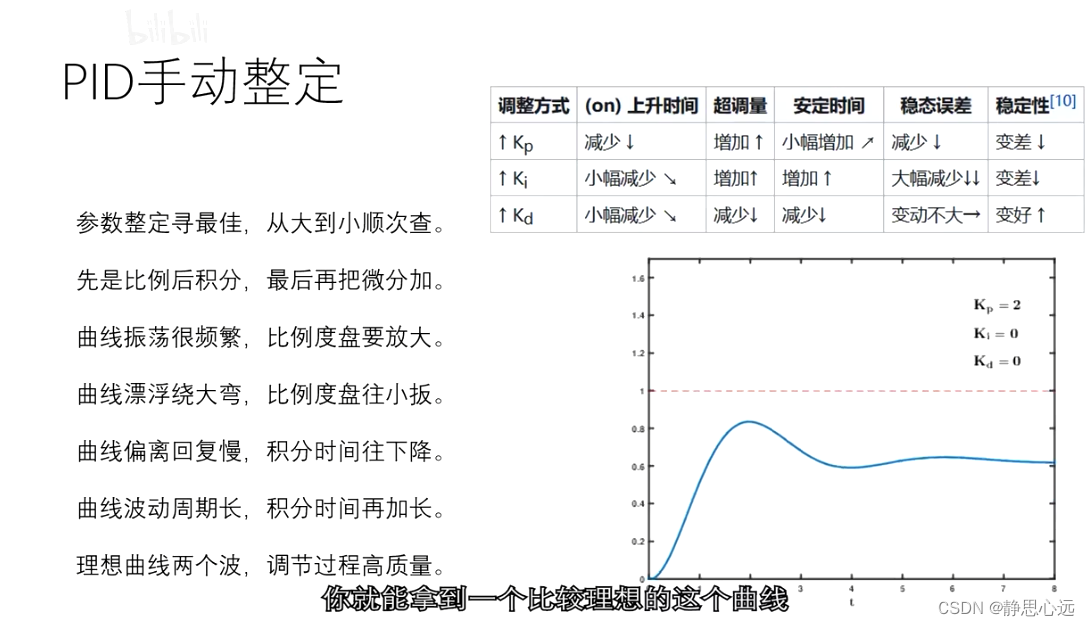
PID调试口诀：
参数整定找最佳， 从小到大顺序查。
先是比例后积分， 最后再把微分加。
曲线振荡很频繁， 比例度盘要放大。
曲线漂浮绕大弯， 比例度盘往小扳。
曲线偏离回复慢， 积分时间往下降。
曲线波动周期长， 积分时间再加长。
曲线振荡频率快， 先把微分降下来。
动差大来波动慢， 微分时间应加长。
理想曲线两个波， 前高后低四比一。
一看二调多分析， 调节质量不会低。

4、reference

• 优快云博主「小 隆隆」 Python代码实现PID控制
• 使用python模拟实现PID控制算法
• Python十行代码实现简单卡尔曼滤波（Kalman Filter）
• PID控制学习笔记之四—位置式PID
• 位置式和增量式PID算法