误差和梯度下降

最新推荐文章于 2022-08-19 12:19:43 发布

原创

最新推荐文章于 2022-08-19 12:19:43 发布 · 337 阅读

0 ·

CC 4.0 BY-SA版权

博客探讨了误差的来源，包括Bias和Variance的概念，解释了如何判断过拟合和欠拟合，并介绍了梯度下降法，如L损失函数、学习率调整和自适应学习率策略。此外，还提到了特征缩放对随机梯度下降模型收敛速度的影响。

误差的来源

Bias + Variance

模型最理想状态是没有bias，而且Variance 很小

Variance 方差

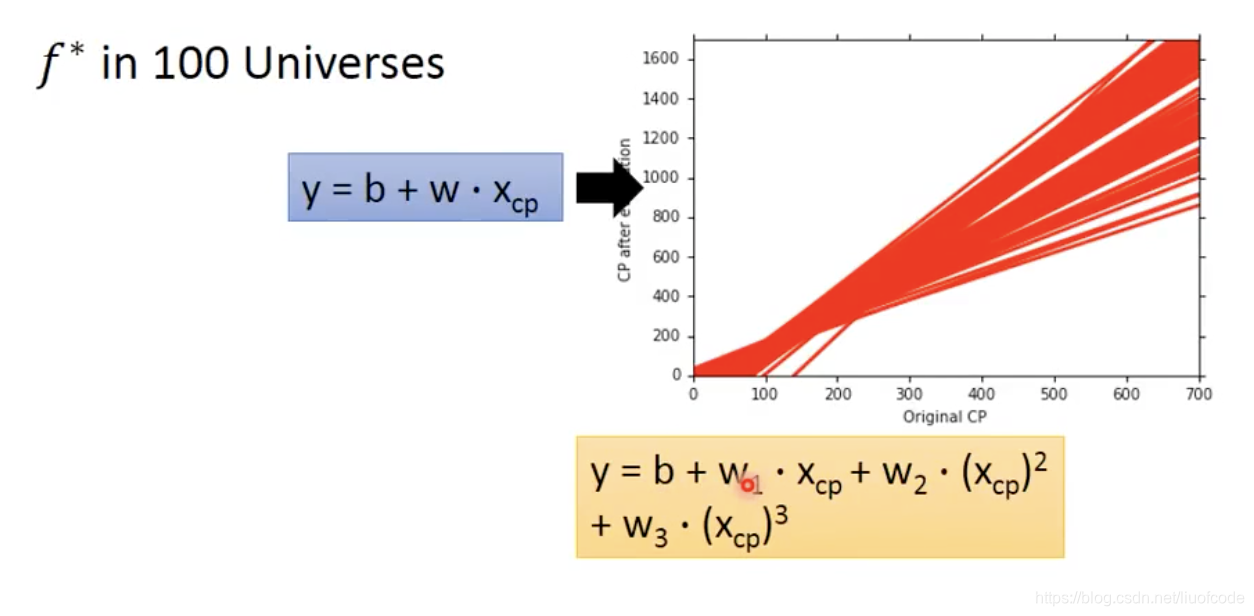
简单的模型的variance 就偏小。

模型越简单，特征越少，所以受数据的方法影响越小

Bias

数据集的均值和测试集的均值的欧式距离就是Bias的大小

模型越复杂，特征越多，Bias 越小

Bias 和 Variance 造成了过拟合和和欠你和。Bias 大就是欠拟合，Variance 就是过拟合

判断过拟合或者欠拟合的方法

方差大加数据，正则化，流型，PCA

Bias大加特征

模型选择

交叉验证

梯度下降 Gradient Descent

$\theta^{*}=argminL(\theta )$ L loss function

调整学习率

学习率不能太大防止跨过收敛值，学习率太小，模型训练时间太长

自适应学习率

举一个简单的思想：随着次数的增加，通过一

最低0.47元/天解锁文章

确定要放弃本次机会？

福利倒计时

: :

立减 ¥

普通VIP年卡可用

立即使用

liuofcode

关注关注

0
点赞
踩
0

收藏

觉得还不错? 一键收藏
0
评论
分享

复制链接

分享到 QQ

分享到新浪微博

扫一扫
举报

举报

机器学习(三)：误差与梯度下降

qq_43360009的博客

09-18

551

三、偏差与梯度下降 Bias and Variance 一个模型的误差主要来源于两部分：bias and variance bias: 估计值与真实值之间存在的差异 Variance: 描述数据之间的离散程度，即波动范围在实际情况中，我们是通过样本来进行推断，所以得到的结果都是估计值，一般会使用y^\hat yy^的方式来表示。关于bias和variance见下面例子设变量XXX的观测值为x1,x2,⋯ ,xnx_1,x_2,\cdots,x_nx1,x2,⋯,xn, 且真实的均值（期望）为

【李宏毅机器学习CP5-8】(task3上)误差分析+梯度下降优化

发现问题，并解决问题，批判性思维

07-16

1293

学习心得（1）文章目录学习心得一、误差Error分析1.估测变量x的偏差和方差1）评估x的偏差bias2）评估x的方差variable2.不同模型情况1）不同模型的方差2）不同模型的偏差3）方差VS偏差3.判断&分析1）偏差大-欠拟合2）方差大-过拟合4.模型的选择1）交叉验证2）N-折交叉验证二、梯度下降0.复习梯度下降1.梯度下降的数学理论1）泰勒展开式2）利用泰勒展开式化简2.措施1）调整学习速率自适应学习率Adagrad 算法2）随机梯度下降法3）特征放缩三、Gradient Desce

参与评论您还未登录，请先登录后发表或查看评论

误差和梯度下降（李宏毅深度学习task 3）

Yzy_fulture的博客

07-16

1272

误差和梯度下降1. 误差的来源1.1 error (误差)1.2 bias（偏差）1.3 variance （方差）1.4 举例说明1.5 偏差方差困境2 估测2.1 估测X的偏差2.1.1 估测平均值2.1.2 估测方差2.2 为什么会有多个模型3 判断分析3.1 欠拟合-偏差大3.2 过拟合4 比较检验4.1 交叉验证4.2 N折交叉验证5. 梯度下降5.1 学习率的调整（η\etaη）5.1.1 一般学习率的调整5.1.2 自适应调整学习率5.2 随机梯度下降法5.3 特征缩放5.3.1 缩放的原因

误差与梯度下降

梦码城博客中心

10-15

2683

误差误差＝方差＋偏差2 + 噪音组成，一般来说，随着模型复杂度的增加，方差会逐渐增大，偏差会逐渐减小偏差（Bias）偏差（bias）：偏差衡量了模型的预测值与实际值之间的偏离关系。通常在深度学习中，我们每一次训练迭代出来的新模型，都会拿训练数据进行预测，偏差就反应在预测值与实际值匹配度上，比如通常在keras运行中看到的准确度为96%，则说明是低偏差；反之，如果准确度只有70%，则说明是高偏差。方差（Variance）方差（variance）：方差描述的是训练数据在不同迭代阶段的训练模

1.1.二分类的成本误差和梯度下降法1

08-03

"二分类的成本误差和梯度下降法" 二分类的成本误差和梯度下降法是机器学习中的一种常见算法，用于解决二分类问题。该算法的主要思想是，通过找到合适的参数，使得输出结果尽可能接近真实值。首先，我们需要了解二...

深度学习-误差和梯度下降

weixin_46435816的博客

07-17

791

深度学习-误差和梯度下降 1.关于Error 1.1 偏差和方差什么是偏差和方差：偏差和方差的区别如下图所示，在简单模型（左边）是偏差比较大造成的误差，这种情况叫做欠拟合，而复杂模型（右边）是方差过大造成的误差，这种情况叫做过拟合。 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gAG9arZ7-1626346348640)(C:\Users\XP_Fan\Desktop\chapter5-12.png)] 1.2 如何进行分析 [外链图片转存失败,源站可能有防盗链机制,

吴恩达机器学习课程CODE1：线性回归算法（应用平方误差与梯度下降）

12-22

1.线性回归问题课程笔记 1）简单介绍线性回归问题需要有一个真实的直线来对给定x求出y，但现在我们不知道这条直线，需要根据训练集去拟合一条无限逼近这条真实直线的直线，以用于预测。如图根据训练集，力求得到一...

误差来源和梯度下降法

weixu22的博客

07-16

767

误差的来源机器学习的目的是学到与任务（预测等）相关的知识，也就是模型。模型的输入应当能贴合实际应用场景，而且有准确的输出。模型效果需要经过严谨的验证才能被使用，然后得出稳健的结论。为了提高模型的性能，使其能够反映真实情况并创造价值，对其误差来源的分析是非常重要的。真实（real）与估测（estimated）对于任何一个具体的任务，我们都相信存在一个“真实模型（real model）”，但这个模型几乎无法获得，只能够去估测。举例来说，pokemon精灵进化后的数值看起来是随机的，但背后肯定也是制作公司

机器学习（6）--误差与梯度下降

NPU 研0

08-19

500

泛化误差与梯度下降法

李宏毅机器学习-误差和梯度下降

DongXueL的博客

05-20

524

目录前言一、误差 1.偏差 2.方差 3.减少错误 4.模型选择（比较验证）（1）交叉验证（2）N折交叉验证二、梯度下降 1.调整学习率（1）一般调整学习率（2）自适应学习率（3）Adagrad算法 2.随机梯度下降 3.特征缩放总结前言本文内容涉及误差、梯度下降，来源于李宏毅老师深度学习视频。一、误差误差反映整个模型的准确度，误差的来源由两部分：偏差（bias）和方差（variance）。可以用下面式子表示： 1.偏差描述

李宏毅机器学习笔记 3.误差和梯度下降

weixin_43983838的博客

08-22

509

最近在跟着Datawhale组队学习打卡，学习李宏毅的机器学习/深度学习的课程。课程视频：https://www.bilibili.com/video/BV1Ht411g7Ef 开源内容：https://github.com/datawhalechina/leeml-notes 本篇文章对应视频中的P5-8。另外，最近我也在学习邱锡鹏教授的《神经网络与深度学习》，会补充书上的一点内容。通过上一次课2.回归，我们了解到机线性回归中的（1）损失函数、（2）梯度下降、（3）过拟合和正则化。本篇文章主要介绍.

李宏毅机器学习03、04-误差和梯度下降

weixin_43243315的博客

09-17

638

李宏毅机器学习03、04-误差和梯度下降 误差误差来源误差有三个来源：样本噪音noise；模型预测值的方差variance；预测值相对真实值的偏差bias。误差计算公式：误差的期望值 = 噪音的方差 + 模型预测值的方差 + 预测值相对真实值的偏差的平方 E((y−f^(x))2)=σ2+Var[f^(x)]+(Bias[f^(x)])2Bias[f^(x)]=E[f^(x)−f(x)] E((y−\hat f(x))^2)=σ^2+Var[\hat f(x)]+(Bias[\hat f(

Task03:误差及梯度

m0_57050414的博客

08-18

674

一、误差的来源： error=偏差 bias+ 方差 variance 二、不同模型的偏差和方差方差：取决于model的复杂度和 data的数量较简单的model：比较集中，离散程度比较小，方差小较复杂的model：比较分散，离散程度大，方差大结论：简单的model 受到不同的training set的影响是较小的偏差：取决于model的复杂度简单的model：简单model...

梯度下降（Gradient Descent）

n不正

04-12

1290

梯度下降（Gradient Descent）1 Gradient Descent θ∗=argminθL(θ)\theta^* = \mathop{argmin}\limits_{\theta} L(\theta) θi=θi−1−η∇L(θi−1)\theta_i =\theta_{i-1} - \eta \nabla L(\theta_{i-1}) 2 Tips Learning Rate 学习

梯度下降（详解）

热门推荐

10-25

3万+

机器学习中我们经常可以看见梯度下降这个名词，但是什么是梯度下降？梯度下降是用来干什么的？网上一大堆文章，看到最后也没看出个名堂出来，刚好今天看到了篇文章，然后结合自己的一些理解，记录下。【什么是梯度下降】首先我们可以把梯度下降拆解为梯度+下降，那么梯度可以理解为导数（对于多维可以理解为偏导），那么合起来变成了：导数下降，那问题来了，导数下降是干什么的？这里我直接给出答案：梯度下降就是用来求某个函数最小值时自变量对应取值其中这句话中的某个函数是指：损失函数（cost/loss function），

采用梯度下降法训练，逻辑回归模型时，loss越来越大，怎么回事？

Kp0fS的草稿纸

08-07

1765

坑

梯度爆炸和梯度消失——引入的误差越来越多，同时有用信息减少，同时想到的了relay BP

gaotihong的博客

10-30

1036

这个将是对于用基于梯度优化方法的死结。 https://machinelearningmastery.com/exploding-gradients-in-neural-networks/ 爆炸梯度是一个问题，其中大的误差梯度累积并导致在训练期间对神经网络模型权重的非常大的更新。这会导致您的模型不稳定，无法从您的训练数据中学习。在这篇文章中，您将发现使用深度人工神经网络爆炸梯度的问题。...

误差反向传播算法（BP）和梯度下降算法

qq_25639051的博客

08-12

3365

为什么需要反向传播算法在多层感知器中，输入数据从输入层输入，经过中间层（隐层），最终从输出层输出。但是由于误差修正学习无法跨层调整，因此修正学习法一般只用于中间层（隐层）与输出层之间，而输入和中间层之间的连接权重采用随机数确定，这就存在输入数据不同，但在中间层的值却相同的问题，影响分类准确性。针对该问题，鲁梅尔哈特的人于1986年提出了误差反向传播算法，该算法使得神经网络再次回到人们的视野。什么是误差反向传播算法？通过比较实际输出和期望输出得到的误差信号，把误差信号从输出层逐层向前传播,得到各层的误差

二分类问题与逻辑回归：理解成本误差和梯度下降

"这篇资料主要介绍了二分类问题中的成本误差和梯度下降法，并结合Python环境进行了阐述。在图像识别的场景中，我们要预测图片中是否含有猫，通过将RGB矩阵转换为列向量作为输入x，用0或1表示类别y。数据集由多个样本...