强化学习中的基于表格型的规划和学习
1. 引言
在强化学习中,规划(Planning)和学习(Learning)是两个核心概念:
- 规划:利用环境模型来改进策略
- 学习:直接从经验中改进策略
规划例如我们前面说的MDP还有DP,都是直接在没有任何的实际的情况的下直接对策略进行的改进。学习则是我们最近几章搞的学习的东西
这两种方法并不是对立的,而是可以结合使用的,这就是本章的核心内容。
2. 模型与规划
开始之前 ,我们先讨论一个概念叫做 “采样模型”,使我们用来模拟一个采样返回的情况的模型,比如我们存放的过去的经验,就是一个采样模型。
对比真实的情况,采样模型的区别在于,我们可以从任意的状态s和a开始采样,得到返回的概率分布,但是不会对实际的结果产生任何的影响
2.1 什么是模型?
模型是对环境的模拟,包含两个关键部分:
- 状态转移函数 P(s’|s,a):在状态s下采取动作a后转移到状态s’的概率
- 奖励函数 R(s,a,s’):从s经过动作a转移到s’获得的奖励
模型可以表示为:
P_{ss'}^a = P(s'|s,a)
R_{ss'}^a = E[R_{t+1}|S_t=s, A_t=a, S_{t+1}=s']
2.2 规划的基本方法
规划主要使用动态规划方法,包括两种基本操作:
- 策略评估:计算某个策略的价值函数
- 策略改进:根据价值函数改进策略
2.3 随机采样单步表格型Q规划
这个内容和前面学习到的Q学习基本上一模一样,只是这里学习的是模型采样,前面学习的是实际采样。收敛条件也是一样:需要保证所有的动作多有可能无限次数的被选中
3. Dyna架构
其实Q学习的重大的问题就是很多稀疏奖励的函数出现的概率本来就很低,所以如果能多次播放,则会产生很大的优势
3.1 基本概念
Dyna是一个结合规划和学习的框架,它同时使用:
- 真实经验:与环境交互获得的样本
- 模拟经验:使用模型生成的样本
3.2 Dyna-Q算法
Dyna-Q算法对比Q-学习的算法,只是额外增加了一个类似于经验回放的机制,但是这里的经验回放的机制是不准确的,原文是Model(S,A) --> R,S`,产生的新的R,S是基于Model去计算的,而去计算的原则从最基本的逻辑上来思考就是频率代替概率,经常学习大数定律的人都知道,这个是有数学基础的~~~~哈哈哈
具体的算法如下,无论是你记录了出现的次数,还是保存了全部的概率然后完全随机,本质上就是一个东西
def Dyna_Q(n_planning_steps):
# 初始化Q表和模型
Q = initialize_q_table()
Model = initialize_model()
while not done:
# 1. 与环境交互
s = current_state
a = epsilon_greedy(Q[s])
s_next, r = env.step(a)
# 2. 直接RL更新
Q[s][a] += alpha * (r + gamma * max(Q[s_next]) - Q[s][a])
# 3. 更新模型
Model.update(s, a, s_next, r)
# 4. 规划步骤
for _ in range(n_planning_steps):
s_plan = random_state_from_memory()
a_plan = random_action_from_memory(s_plan)
s_next_plan, r_plan = Model.predict(s_plan, a_plan)
# 使用模型数据更新Q表
Q[s_plan][a_plan] += alpha * (r_plan + gamma * max(Q[s_next_plan]) - Q[s_plan][a_plan])
3.3 Dyna的优势
- 数据效率:每个真实样本都被多次使用
- 计算和实际交互的平衡:可以通过调整规划步数来平衡
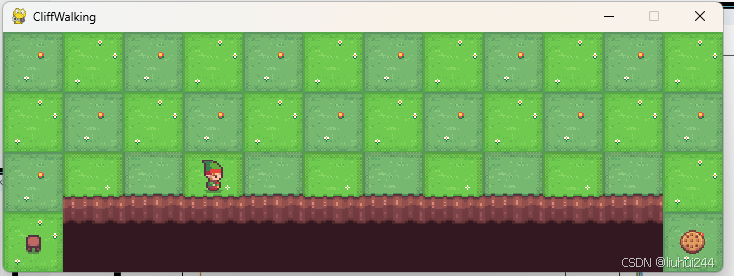
3.4使用Dyna-Q來实现cliff walking
环境直接使用的gym的环境,下图是真实的render的图像展示
可以明显看到,在planning步长更长的情况,收敛的更加快速,并且reward更加的
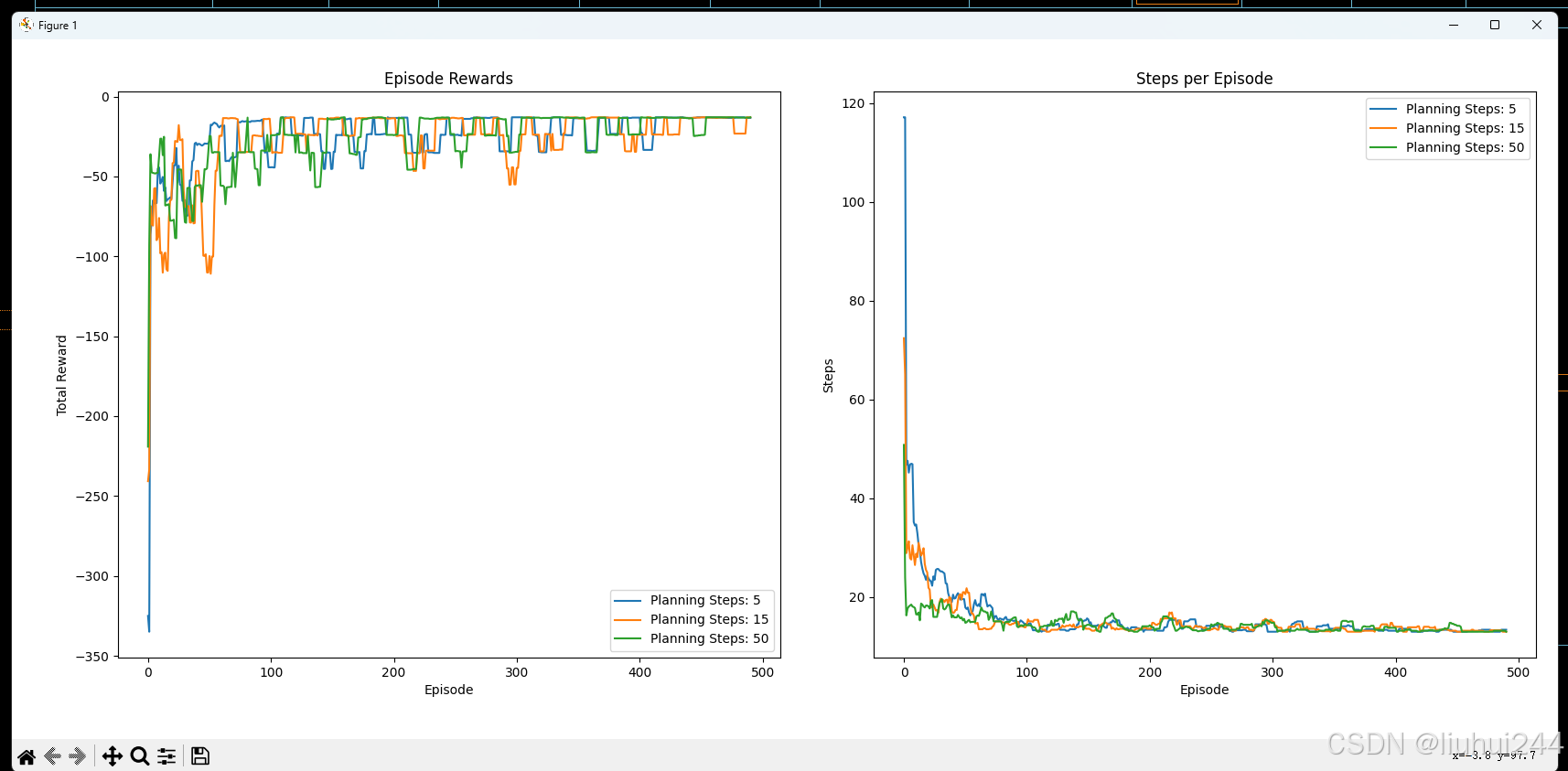
放一下我的运行的源代码,大家可以参考实现,注意,每次只是保存最新的情况s,a的情况而不会继续保存其他的情况,这只是一个方式,你们可以有其他的想法,原文中也是这么提到,总是立即对最新的传感信息给予反馈
import numpy as np
import gymnasium as gym
import matplotlib.pyplot as plt
from tqdm import tqdm
class DynaQ:
def __init__(self, n_states, n_actions, learning_rate=0.1, gamma=0.95,
epsilon=0.1, n_planning_steps=50):
self.n_states = n_states
self.n_actions = n_actions
self.lr = learning_rate
self.gamma = gamma
self.epsilon = epsilon
self.n_planning_steps = n_planning_steps
# Q表和模型
self.q_table = np.zeros((n_states, n_actions))
self.model = {} # 存储(s,a) -> (r,s',done)的映射
self.experienced_sa_pairs = set()
def choose_action(self, state):
"""ε-贪婪策略选择动作"""
if np.random.random() < self.epsilon:
return np.random.randint(self.n_actions)
return np.argmax(self.q_table[state])
def learn(self, state, action, reward, next_state, done):
"""实际经验学习"""
# 更新Q表
target = reward
if not done:
target += self.gamma * np.max(self.q_table[next_state])
self.q_table[state, action] += self.lr * (target - self.q_table[state, action])
# 更新模型
self.model[(state, action)] = (reward, next_state, done)
self.experienced_sa_pairs.add((state, action))
# 规划更新
self.planning()
def planning(self):
"""使用模型进行规划"""
if len(self.experienced_sa_pairs) == 0:
return
# 随机选择已经体验过的状态-动作对进行规划
sa_pairs = list(self.experienced_sa_pairs)
n_samples = min(self.n_planning_steps, len(sa_pairs))
for _ in range(n_samples):
# 随机选择一个已经体验过的状态-动作对
idx = np.random.randint(len(sa_pairs))
state, action = sa_pairs[idx]
# 使用模型获得奖励和下一个状态
reward, next_state, done = self.model[(state, action)]
# Q-learning更新
target = reward
if not done:
target += self.gamma * np.max(self.q_table[next_state])
self.q_table[state, action] += self.lr * (target - self.q_table[state, action])
def train_dyna_q(env, agent, episodes, render=False):
"""训练函数"""
episode_rewards = []
episode_steps = []
for episode in tqdm(range(episodes), desc="Training"):
state, _ = env.reset()
total_reward = 0
steps = 0
done = False
truncated = False
while not (done or truncated):
# 选择动作
action = agent.choose_action(state)
# 执行动作
next_state, reward, done, truncated, _ = env.step(action)
if render and episode % 100 == 0:
env.render()
# 学习
agent.learn(state, action, reward, next_state, done)
total_reward += reward
steps += 1
state = next_state
episode_rewards.append(total_reward)
episode_steps.append(steps)
# 衰减探索率
agent.epsilon = max(0.01, agent.epsilon * 0.995)
return episode_rewards, episode_steps
def plot_results(results):
"""绘制训练结果"""
plt.figure(figsize=(12, 5))
window_size = 10
# 计算滑动平均
# 绘制奖励
for rewards, steps, planning_steps in results:
avg_rewards = np.convolve(rewards, np.ones(window_size)/window_size, mode='valid')
avg_steps = np.convolve(steps, np.ones(window_size)/window_size, mode='valid')
plt.subplot(121)
plt.plot(avg_rewards, label=f'Planning Steps: {planning_steps}')
plt.title('Episode Rewards')
plt.xlabel('Episode')
plt.ylabel('Total Reward')
plt.legend()
# 绘制步数
plt.subplot(122)
plt.plot(avg_steps, label=f'Planning Steps: {planning_steps}')
plt.title('Steps per Episode')
plt.xlabel('Episode')
plt.ylabel('Steps')
plt.legend()
plt.tight_layout()
plt.show()
def evaluate_agent(env, agent, n_episodes=10):
"""评估函数"""
total_rewards = []
total_steps = []
for _ in range(n_episodes):
state, _ = env.reset()
episode_reward = 0
steps = 0
done = False
truncated = False
while not (done or truncated):
action = np.argmax(agent.q_table[state]) # 使用贪婪策略
next_state, reward, done, truncated, _ = env.step(action)
episode_reward += reward
steps += 1
state = next_state
total_rewards.append(episode_reward)
total_steps.append(steps)
return np.mean(total_rewards), np.mean(total_steps)
if __name__ == "__main__":
# 创建环境和智能体
env = gym.make('CliffWalking-v0')
results = []
for planning_steps in [5, 15, 50]:
agent = DynaQ(
n_states=env.observation_space.n,
n_actions=env.action_space.n,
learning_rate=0.1,
gamma=0.95,
epsilon=0.1,
n_planning_steps=planning_steps
)
# 训练
print("Starting training...")
rewards, steps = train_dyna_q(env, agent, episodes=500)
results.append((rewards, steps, planning_steps))
# 绘制结果
plot_results(results)
# 评估
print("\nEvaluating agent...")
avg_reward, avg_steps = evaluate_agent(env, agent)
print(f"Average evaluation reward: {avg_reward:.2f}")
print(f"Average evaluation steps: {avg_steps:.2f}")
# 可视化最终策略
print("\nFinal policy:")
state, _ = env.reset()
env = gym.make('CliffWalking-v0', render_mode='human')
state, _ = env.reset()
done = False
truncated = False
while not (done or truncated):
action = np.argmax(agent.q_table[state])
state, _, done, truncated, _ = env.step(action)
env.render()
3.5 Dyna-Q+
为什么要有这个新的模型,因为我们知道学习到的模型是会变的,比如迷宫的起始地址,比如迷宫的环境变化,或者悬崖的位置等等,那么如果模型没有强大的试错的能力,那么很有可能会无法纠正路线,或者困在过去的经验里面
Dyan-Q则是增加了一个随着时间增加的未访问的回报k
t
\sqrt{t}
t,t是这个状态么有被访问的事件,k是我们选择的一个尝试的系数。好奇心是需要计算的代价的
4. 优先清单规划
优先清单的规划是这样的,显然不是所有的动作都是一样的优先级,因为有些动作例如稀疏的奖励的最后的奖励的时刻,那么我们可以给不同的回放经验也好,特定的s,a,r,s`也好,我们可以通过配置不同的优先级来完成对于特殊经验的学习,对终点进行反向更新或许是一个非常好的学习的方法,称之为反向聚焦
4.1 优先清单的概念
不是随机选择状态-动作对进行规划,而是根据优先级选择。优先级基于:
- 时序差分误差的大小
- 状态的访问频率
- 价值变化的幅度
4.2 优先清单Dyna算法
原文中的算法里面提到了一个很重要的点,那就是前向更新 S ˉ , A ˉ \bar S,\bar A Sˉ,Aˉ是到到达应该加入到优先队列的S,A的前向的可能性
def PrioritizedSweeping_Dyna():
PQueue = PriorityQueue() # 优先队列
while True:
# 1. 真实交互和更新
s, a, s_next, r = get_experience()
# 2. 计算优先级
p = r + gamma * max(Q[s_next]) - Q[s][a]|
# 3. 如果优先级大于阈值,加入队列
if p > threshold:
PQueue.insert(s, a, p)
# 4. 规划步骤
for _ in range(n_planning_steps):
if PQueue.empty():
break
s, a = PQueue.pop() # 取出最高优先级的状态-动作对
# 更新Q值并可能将前继状态加入队列
数学表达式,实际上是
δ
\delta
δ的大小
p
r
i
o
r
i
t
y
=
r
+
γ
max
a
Q
(
s
′
,
a
)
−
Q
(
s
,
a
)
∣
priority = r + \gamma \max_a Q(s',a) - Q(s,a)|
priority=r+γmaxaQ(s′,a)−Q(s,a)∣
4.3 Dyna-Q + 优先清扫
在原本的基础上增加了优先清扫的功能,但是这里有个问题就是我们的的奖励一直都是-1,导致每一个步的收益很不明显,要选择合适的priority的阈值,否则很不容易使用到优先队列,
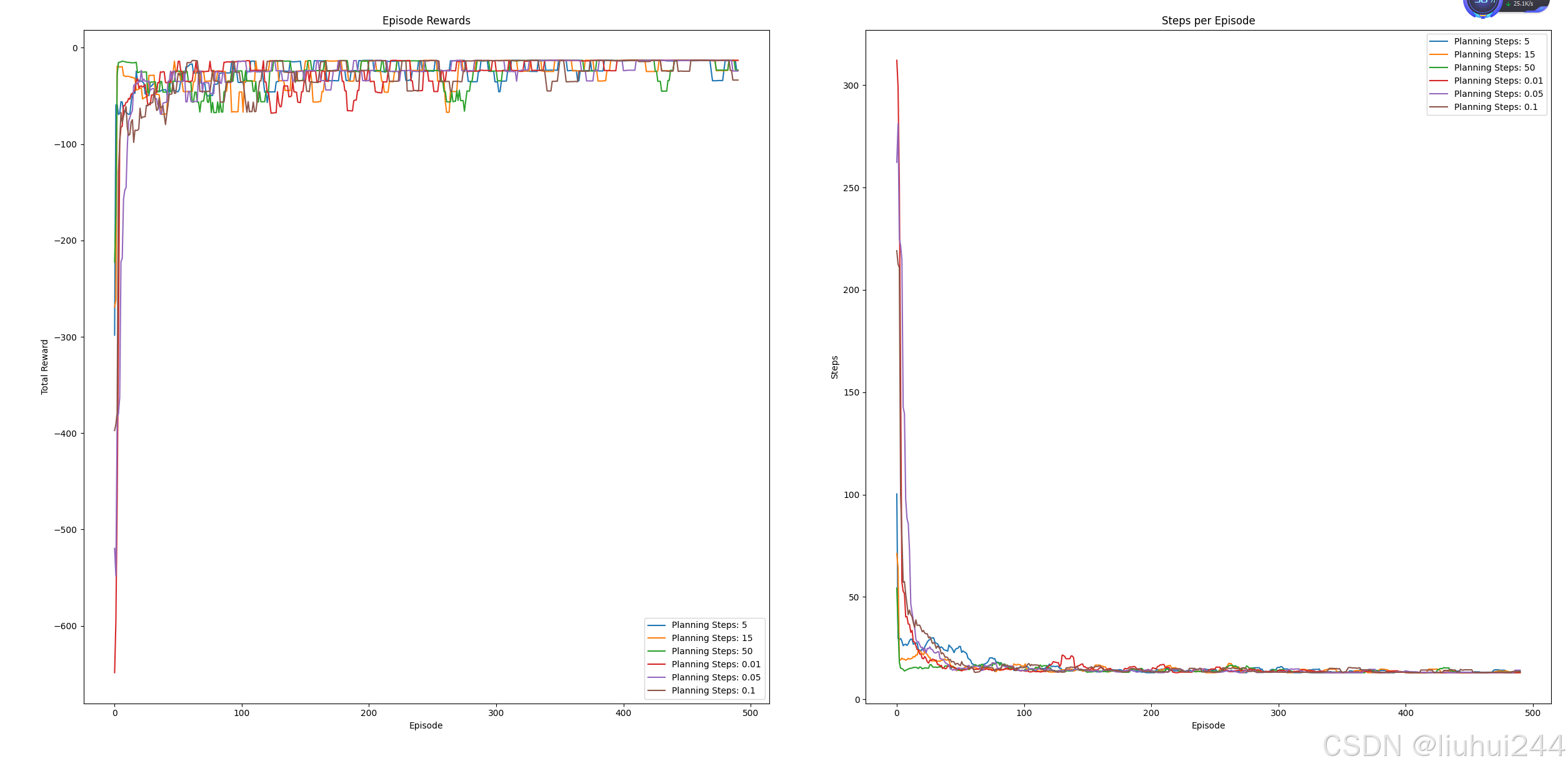
代码实现如下,我中间踩了很多坑
比如合适的kappa值,比如要使用前置的队列,比如更新的顺序和添加节点的方式
import numpy as np
import gymnasium as gym
import matplotlib.pyplot as plt
from tqdm import tqdm
import heapq
class DynaQ:
def __init__(self, n_states, n_actions, learning_rate=0.1, gamma=0.95,
epsilon=0.1, n_planning_steps=50):
self.n_states = n_states
self.n_actions = n_actions
self.lr = learning_rate
self.gamma = gamma
self.epsilon = epsilon
self.n_planning_steps = n_planning_steps
# Q表和模型
self.q_table = np.zeros((n_states, n_actions))
self.model = {} # 存储(s,a) -> (r,s',done)的映射
self.experienced_sa_pairs = set()
def choose_action(self, state):
"""ε-贪婪策略选择动作"""
if np.random.random() < self.epsilon:
return np.random.randint(self.n_actions)
return np.argmax(self.q_table[state])
def learn(self, state, action, reward, next_state, done):
"""实际经验学习"""
# 更新Q表
target = reward
if not done:
target += self.gamma * np.max(self.q_table[next_state])
self.q_table[state, action] += self.lr * (target - self.q_table[state, action])
# 更新模型
self.model[(state, action)] = (reward, next_state, done)
self.experienced_sa_pairs.add((state, action))
# 规划更新
self.planning()
def planning(self):
"""使用模型进行规划"""
if len(self.experienced_sa_pairs) == 0:
return
# 随机选择已经体验过的状态-动作对进行规划
sa_pairs = list(self.experienced_sa_pairs)
n_samples = min(self.n_planning_steps, len(sa_pairs))
for _ in range(n_samples):
# 随机选择一个已经体验过的状态-动作对
idx = np.random.randint(len(sa_pairs))
state, action = sa_pairs[idx]
# 使用模型获得奖励和下一个状态
reward, next_state, done = self.model[(state, action)]
# Q-learning更新
target = reward
if not done:
target += self.gamma * np.max(self.q_table[next_state])
self.q_table[state, action] += self.lr * (target - self.q_table[state, action])
class DynaQPlus(DynaQ):
def __init__(self, n_states, n_actions, learning_rate=0.1, gamma=0.95,
epsilon=0.1, n_planning_steps=50, kappa=0.001):
super().__init__(n_states, n_actions, learning_rate, gamma, epsilon, n_planning_steps)
self.kappa = kappa
# 优先队列使用堆实现
self.priority_queue = []
# 存放到达这个状态的前置状态-动作对
self.pre_state_action_pairs = {}
def reset_priority_queue(self):
self.priority_queue = []
def reset_experienced_sa_pairs(self):
self.experienced_sa_pairs = set()
def choose_action(self, state):
if np.random.random() < self.epsilon:
return np.random.randint(self.n_actions)
return np.argmax(self.q_table[state])
def learn(self, state, action, reward, next_state, done):
if done:
reward += 10
# 更新模型
self.model[(state, action)] = (reward, next_state, done)
self.experienced_sa_pairs.add((state, action))
# 更新到达这个状态的前置状态-动作对
if next_state not in self.pre_state_action_pairs:
self.pre_state_action_pairs[next_state] = []
self.pre_state_action_pairs[next_state].append((state, action))
# 更新TD误差
if not done:
td_error = reward + self.gamma * np.max(self.q_table[next_state]) - self.q_table[state, action]
else:
td_error = reward - self.q_table[state, action]
#print(reward, td_error)
# 学习
self.q_table[state, action] += self.lr * (td_error)
# 按照对于能到达这个状态的前置状态-动作对进行排序插入优先队列
if td_error > self.kappa:
for pre_state, pre_action in self.pre_state_action_pairs[state]:
heapq.heappush(self.priority_queue, (-td_error, (pre_state, pre_action)))
self.planning()
def planning(self):
"""使用优先队列 模型进行规划"""
if len(self.priority_queue) == 0:
return
for _ in range(min(self.n_planning_steps, len(self.priority_queue))):
#从优先队列中取出TD误差最大的状态-动作对
td_error, (state, action) = heapq.heappop(self.priority_queue)
# 使用模型获得奖励和下一个状态
reward, next_state, done = self.model[(state, action)]
# Q-learning更新
if not done:
td_error = reward + self.gamma * np.max(self.q_table[next_state]) - self.q_table[state, action]
else:
td_error = reward - self.q_table[state, action]
self.q_table[state, action] += self.lr * (td_error)
if td_error > self.kappa:
for pre_state, pre_action in self.pre_state_action_pairs[state]:
heapq.heappush(self.priority_queue, (-td_error, (pre_state, pre_action)))
return
def train_dyna_q(env, agent, episodes, render=False):
"""训练函数"""
episode_rewards = []
episode_steps = []
for episode in tqdm(range(episodes), desc="Training"):
state, _ = env.reset()
total_reward = 0
steps = 0
done = False
truncated = False
while not (done or truncated):
# 选择动作
action = agent.choose_action(state)
# 执行动作
next_state, reward, done, truncated, _ = env.step(action)
if render and episode % 100 == 0:
env.render()
# 学习
agent.learn(state, action, reward, next_state, done)
total_reward += reward
steps += 1
state = next_state
episode_rewards.append(total_reward)
episode_steps.append(steps)
# 衰减探索率
agent.epsilon = max(0.01, agent.epsilon * 0.995)
return episode_rewards, episode_steps
def plot_results(results):
"""绘制训练结果"""
plt.figure(figsize=(12, 5))
window_size = 10
# 计算滑动平均
# 绘制奖励
for rewards, steps, planning_steps in results:
avg_rewards = np.convolve(rewards, np.ones(window_size)/window_size, mode='valid')
avg_steps = np.convolve(steps, np.ones(window_size)/window_size, mode='valid')
plt.subplot(121)
plt.plot(avg_rewards, label=f'Planning Steps: {planning_steps}')
plt.title('Episode Rewards')
plt.xlabel('Episode')
plt.ylabel('Total Reward')
plt.legend()
# 绘制步数
plt.subplot(122)
plt.plot(avg_steps, label=f'Planning Steps: {planning_steps}')
plt.title('Steps per Episode')
plt.xlabel('Episode')
plt.ylabel('Steps')
plt.legend()
plt.tight_layout()
plt.show()
def evaluate_agent(env, agent, n_episodes=10):
"""评估函数"""
total_rewards = []
total_steps = []
for _ in range(n_episodes):
state, _ = env.reset()
episode_reward = 0
steps = 0
done = False
truncated = False
while not (done or truncated):
action = np.argmax(agent.q_table[state]) # 使用贪婪策略
next_state, reward, done, truncated, _ = env.step(action)
episode_reward += reward
steps += 1
state = next_state
total_rewards.append(episode_reward)
total_steps.append(steps)
return np.mean(total_rewards), np.mean(total_steps)
if __name__ == "__main__":
# 创建环境和智能体
env = gym.make('CliffWalking-v0')
results = []
for planning_steps in [5,15,50]:
agent = DynaQ(
n_states=env.observation_space.n,
n_actions=env.action_space.n,
learning_rate=0.1,
gamma=0.95,
epsilon=0.1,
n_planning_steps=planning_steps
)
# 训练
print("Starting training...")
rewards, steps = train_dyna_q(env, agent, episodes=500)
results.append((rewards, steps, planning_steps))
for kappa in [0.01, 0.05, 0.1]:
agent = DynaQPlus(
n_states=env.observation_space.n,
n_actions=env.action_space.n,
kappa=kappa
)
# 训练
print("Starting training...")
rewards, steps = train_dyna_q(env, agent, episodes=500)
results.append((rewards, steps, kappa))
# 绘制结果
plot_results(results)
# 评估
print("\nEvaluating agent...")
avg_reward, avg_steps = evaluate_agent(env, agent)
print(f"Average evaluation reward: {avg_reward:.2f}")
print(f"Average evaluation steps: {avg_steps:.2f}")
# 可视化最终策略
print("\nFinal policy:")
state, _ = env.reset()
env = gym.make('CliffWalking-v0', render_mode='human')
state, _ = env.reset()
done = False
truncated = False
while not (done or truncated):
action = np.argmax(agent.q_table[state])
state, _, done, truncated, _ = env.step(action)
env.render()
4.4 期望更新与采样更新的对比
不想写这个小节,有人想看我再补充吧
5. 轨迹采样
原文中的例子简直讲的是个蛋疼,我是真的不想总结原文的中的那一部分的东西
5.1 基本概念
不是随机采样状态-动作对,而是沿着实际可能的轨迹进行采样,更符合实际情况。
对比前面的优先清扫队列来看, 更多的不是每次都更新这个节点的可达的节点,而是使用实际的路径上的前置节点来进行更新
本质上我认为轨迹采样就是n步TD,对吧~~~只不过是选择那些有更高的更新的值的情况
5.2 采样方法
-
启发式采样:根据当前策略生成轨迹
启发式采样,简单来说就是通过一定的策略来选择更加值得采样的过程,例如我们可以在走迷宫的环境下,选择那些离终点距离更近的节点来实现,这样可以让我们尽快的处理那些重要的信息,和后面的RTDP的思想不谋而合 -
基于模型的采样:使用环境模型生成完整轨迹
6. 实时动态规划(RTDP)
RTDP就是轨迹采样在DP上的实现的过程,采用了使用轨迹采样的方法进行更新特定的状态,而不是遍历所有的节点的状态来更新V的值,需要说明一下RTDP的收敛的条件
1:每个目标初始值为0
2;存在一个策略使得任意的起始状态可以到达目标状态
3:从非目标状态跳出的转移收益严格为负数
4:初始化状态大于其最优状态
6.1 核心思想
RTDP的方法核心是异步DP,不求获得最优解,而是获取的局部的最优解
RTDP结合了:
- 价值迭代的思想
- 启发式搜索的方法
- 实时更新的特点
6.2 RTDP算法
def RTDP():
while not converged:
s = initial_state
while not terminal(s):
# 选择最佳动作
a = argmax(Q[s])
# 更新当前状态的值
s_next = model.predict(s, a)
V[s] = max(Q[s])
# 移动到下一个状态
s = s_next
7 决策时规划
决策时规划(Planning at Decision Time)的核心是:当需要做一个决策时,才开始进行规划计算,而不是提前算好所有情况。就像下围棋时,只对当前局面进行思考,而不是提前计算所有可能的棋局。
我对决策时的规划的理解很奇怪,因为我觉得这个问题好像就是一个当时的DFS,有点像是,到了一个格子以后,再开始评估当前的周围的几步的情况,来选择下一步的动作。
之前的规划是完整的规划,早在走到这一步之前的时候就已经计算了所有的动作的价值
决策时规划更像是实时性的规划,可能会面对一些对抗或者什么之类的东西,所以每次的价值函数用过以后就已经不再具备实际的意义了,原文中说,可以丢弃。
我理解的是决策时规划更像是基于启发式搜索的DFS的过程,对当前的内容,使用一些函数的价值函数评估不同的动作的场景的价值函数,然后返回一个最优的解,有点像是对抗中的Minmax算法
简单来说,如果需要对模型进行整体的学习是一件很复杂的事情,但是基于一定的规则的近似的状态的计算确实很快的事情,我们使用很快的规划来取代可能无法真正的获取到的价值函数的替代,从而实现短时间的响应程序
决策时规划:
只关注当前状态相关的计算
实时构建局部搜索树
优点:内存效率高
缺点:每次决策都需要计算
其实做算法的人应该都知道,其实就是一直在计算当前的状态的,我觉得这个原文的启发式算法的讲解反而有点绕远了,包括后面的启发式算法树,就是可以简单的理解为基于DFS的启发式算法树而已。
8. 表格型规划和学习的总结
-
关键点:
- 规划和学习的结合
- 模型的使用
- 经验重放的重要性
- 优先级的作用
-
实际应用考虑:
- 计算资源的平衡
- 模型精度的影响
- 实时性要求
- 样本效率






















 1158
1158

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








