2360. 图中的最长环难度困难

最新推荐文章于 2025-12-03 23:35:37 发布

原创最新推荐文章于 2025-12-03 23:35:37 发布 · 456 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #java #算法

本文介绍了一种算法，用于求解给定有向图中的最长环。通过深度优先搜索和回溯机制，该算法能有效地找到图中最长的闭合路径。

给你一个 n 个节点的有向图，节点编号为 0 到 n - 1 ，其中每个节点至多有一条出边。

图用一个大小为 n 下标从 0 开始的数组 edges 表示，节点 i 到节点 edges[i] 之间有一条有向边。如果节点 i 没有出边，那么 edges[i] == -1 。

请你返回图中的最长环，如果没有任何环，请返回 -1 。

一个环指的是起点和终点是同一个节点的路径。

示例 1：

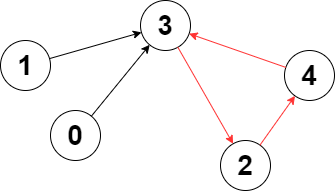
输入：edges = [3,3,4,2,3]
输出去：3
解释：图中的最长环是：2 -> 4 -> 3 -> 2 。
这个环的长度为 3 ，所以返回 3 。
示例 2：

输入：edges = [2,-1,3,1]
输出：-1
解释：图中没有任何环。

public class Demo1 {
    public static void main(String[] args) {
        System.out.println(new Solution().longestCycle(new int[]{3,3,4,2,3}));
    }
}

class Solution {
    static int cnt = 0;
    static Map<Integer, Integer> map = new HashMap<>();
    public int longestCycle(int[] edges) {
        int r = -1;
        map = new HashMap<>();
        for (int i = 0; i < edges.length; i++) {
            Set set = new HashSet();
            cnt = 0;
            int a = dfs(i, i, edges, set);
            map.put(i, a);
            //System.out.println(cnt);
            if (r < a) {
                r = a;
            }
        }
        return r;
    }

    public int dfs(int startIndex, int index, int[] edges, Set set) {
        if (map.get(index) != null) {
            return -1;
        }
        if (index < 0) {
            return -1;
        }
        int cur = edges[index];
        //System.out.println(cur);
        if (cur == -1) {
            return -1;
        }
        if (!set.contains(index)) {
            set.add(index);
            cnt++;
            return dfs(startIndex, cur, edges, set);
        } else {
            if (startIndex != index) {
                return -1;
            } else {
                return cnt;
            }
        }

    }
}