pytorch基础知识的一些笔记

1.什么是张量（Tensor) ？

根据张量的阶数（或秩），可以将其分为以下几类：

1. 零阶张量：也称为标量，它只有一个量值，没有方向。
2. 一阶张量：也称为向量，它既有量值又有方向。
3. 二阶张量：可以看作是一个矩阵，它描述了两个向量之间的线性关系。
4. 高阶张量：阶数大于二的张量，它们在描述更复杂的物理或数学关系时非常有用

在人工智能领域中，张量是基本数据结构，它提供了在模型中存储输入和输出数据的方法。在神经网络中，张量用于表示输入数据、权值和偏差等，为处理各种形式的数据提供了通用的框架。#  https://b23.tv/YGUskIV该视频应该可以有助于理解

2.tensor的定义：tensor(data,*,dtype= , …… ) :

data是数学量，*代表一些其他变量（暂时不用深究），dtype是用来给tensor赋予类型的。……是用来给tensor一些复杂的功能的（暂时也不用深究）。

# dtype可以用来强制转换一些未知变量的类型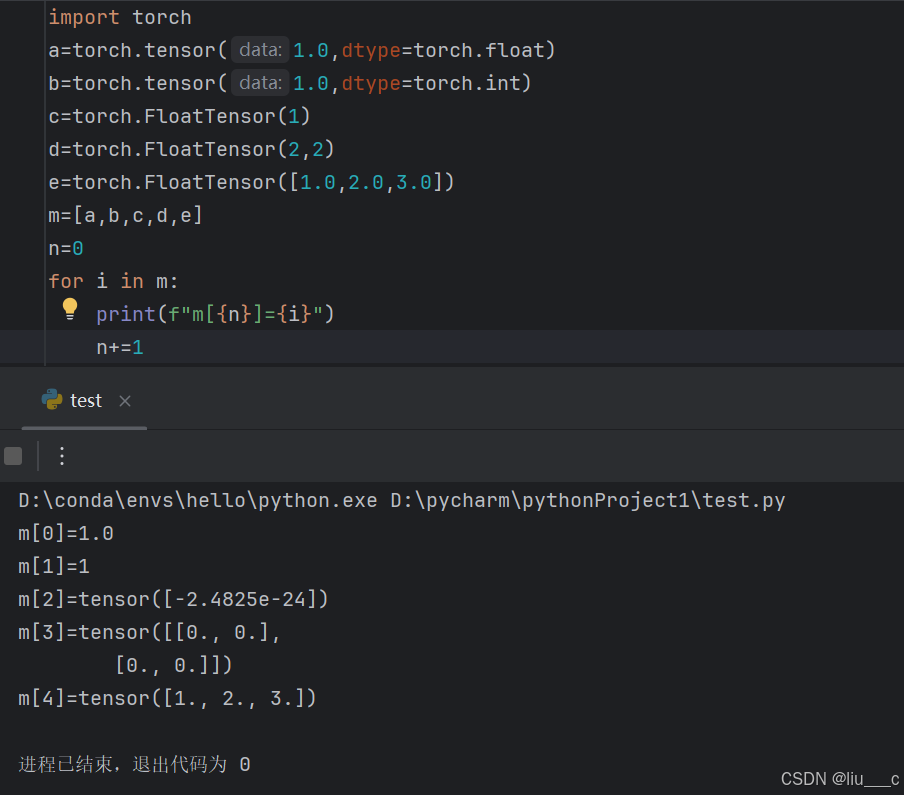

3.numpy是什么

NumPy（Numerical Python的简称）是Python编程语言的一个扩展库，它支持大量的维度数组与矩阵运算，此外也针对数组运算提供大量的数学函数库。

4.numpy创建的变量和tensor创建的变量之间为什么需要转换、转换的好处又是什么？

NumPy创建的变量（通常指ndarray对象）和Tensor（在深度学习框架如PyTorch中）创建的变量之间存在一些关键区别，这些区别主要体现在数据类型、用途、运行环境和初始化方式等方面。

数据类型

• NumPy：
  • 默认的数据类型是float64和int32（尽管可以通过指定dtype参数来改变）。
  • 专门用于科学计算和数据分析，提供了丰富的数学函数库。
• Tensor：
  • 在PyTorch等深度学习框架中，默认的数据类型通常是float32和int64（具体取决于框架和版本）。
  • 主要用于深度学习和神经网络中的数据存储和传递，支持自动求导和梯度计算。

用途

• NumPy：
  • 主要用于数值计算、数据分析、数据预处理等领域。
  • 提供了强大的数组操作、数学函数和统计功能。
• Tensor：
  • 专门用于深度学习和神经网络。
  • 支持在GPU上运行，以实现高效的并行计算。
  • 与深度学习框架（如PyTorch、TensorFlow）的自动求导系统紧密集成。

运行环境

• NumPy：
  • 只能在CPU上运行。
  • 适用于各种计算任务，但缺乏GPU加速。
• Tensor：
  • 可以在CPU和GPU上运行。
  • 深度学习框架通常会自动利用GPU进行加速计算（如果可用）。

初始化方式

• NumPy：
  • 可以通过多种方式初始化数组，包括列表、全零、全一、空数组等。
  • 初始化时需要指定数组的形状和数据类型（可选）。
• Tensor：
  • 在PyTorch中，可以通过指定形状和数据类型来初始化张量。
  • 也可以通过从现有数据（如列表、NumPy数组）中创建张量。
  • 初始化时需要确保数据的形状和类型与指定的张量形状和类型相匹配。

相互转换

• NumPy数组和Tensor之间可以相互转换，且转换过程通常是无缝的（共享内存）。
• 这使得在数据预处理阶段使用NumPy进行数组操作，然后在深度学习模型中使用Tensor进行训练和推理成为可能。

综上所述，NumPy创建的变量和Tensor创建的变量在数据类型、用途、运行环境和初始化方式等方面存在显著差异。这些差异使得它们各自在不同的领域和场景中发挥着重要作用。

# 二者创建的变量都非普通变量。NumPy更适合于一般的数值计算和数据分析任务，而Tensor则更适合于深度学习和神经网络的构建与训练。

5.如何进行numpy和tensor的转换：

# g=……是在创建一个numpy array

# h 和 i都是在将g转化为tensor

# j是在将tensor转化为numpy

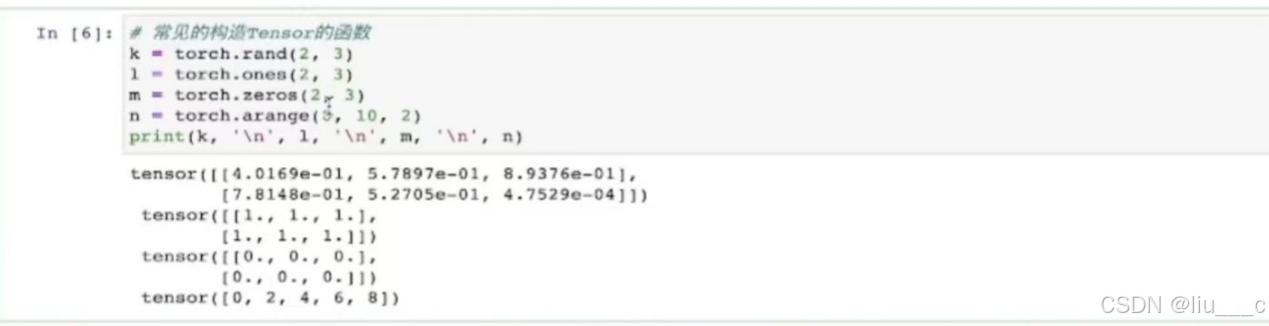
6.一些常见的构造tensor的函数（具体使用效果可由构造结果看出）：

7.查看tensor的维度信息（两种方式）：

#这里的k就是上图的k

8.tensor的索引方式（与numpy类似）：

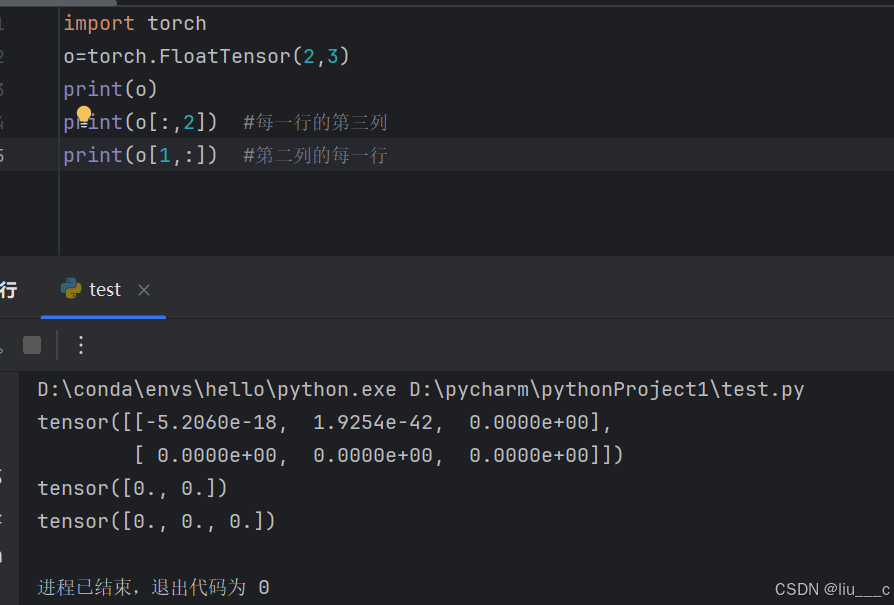
#这里的“ ：“表示全部

9.view的使用（改变tensor形状）

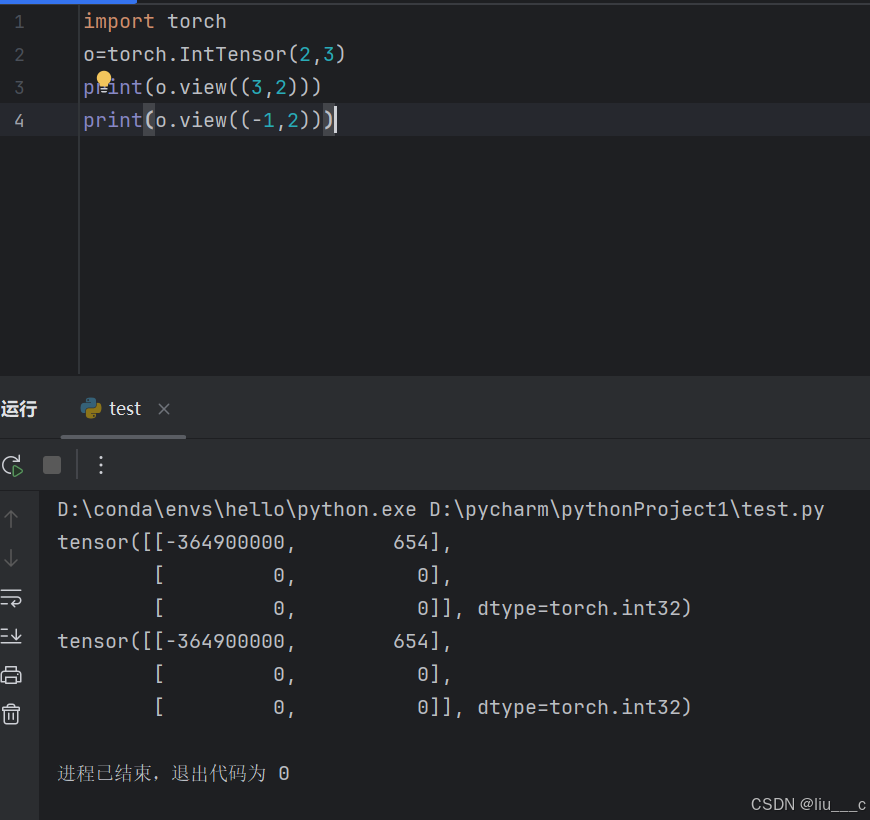
# 以（3，2）和（-1，2）为例，如果确定了2这一维度，懒得算3，可以直接填个-1，计算机会自动填补。

10.tensor 的广播机制

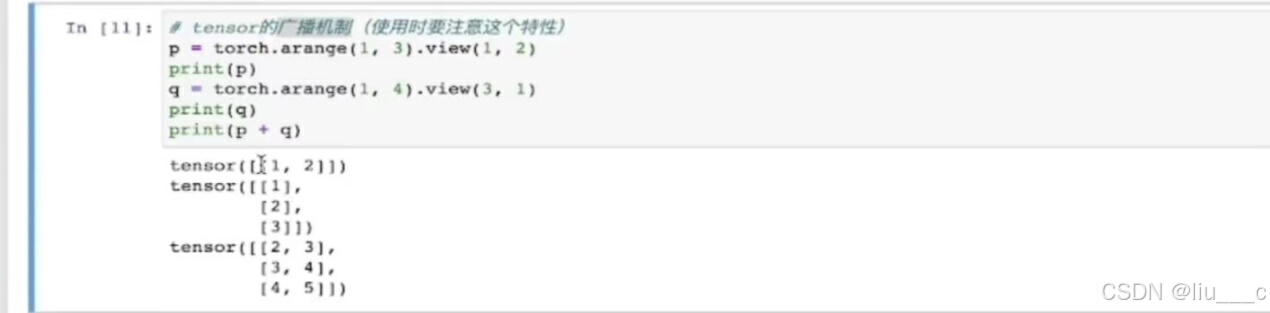
# 得出的结果是二者的公共最大维度（类似最小公倍数吧）

11.什么是张量的维度：

张量的维度，通常简称为张量的“维”或“阶”，是一个描述张量所需坐标数目的概念。

在PyTorch等深度学习框架中，张量的维度是通过其shape属性来指定的，该属性返回一个表示张量在每个维度上大小的元组。

例如，一个形状为(3, 4, 5)的三维张量表示它有3个二维数组（或矩阵），每个矩阵有4行5列。

对于形状 (3, 4, 5) 的张量：

• 第一维 的大小是 3，这意味着张量在这个维度上有 3 个元素。这些元素通常是更高维度的数组（在这个例子中是二维数组，即矩阵）。
• 第二维 的大小是 4，表示每个第一维的元素（即每个矩阵）有 4 行。
• 第三维 的大小是 5，表示每个第一维的元素（即每个矩阵）有 5 列。

12.unsqueeze的使用

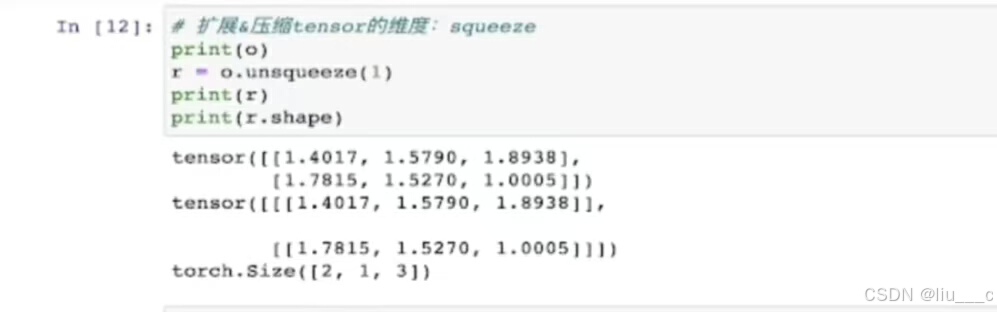
13.squeeze的使用

14.自动求导数学基础：多元函数求导的雅克比矩阵、函数求导链式法则。

15.损失函数反向传播：（还要学习偏导）

一、损失函数

损失函数（Loss Function）是衡量模型预测结果与真实标签之间差距的依据。它的核心作用是告诉我们模型的预测结果“错”得有多离谱。通俗来说，损失函数就像是一个裁判，它给模型的预测结果打分，分数越低，说明模型的预测结果越接近真实情况，模型的性能就越好。

在深度学习中，常用的损失函数包括：

1. L1 Loss（MAE）：平均绝对误差，对异常值的容忍性更高，但当梯度下降恰好为0时无法继续进行。
2. L2 Loss（MSE）：均方误差，连续光滑，方便求导，但易受到异常值的干扰。
3. Smooth L1 Loss：处理异常值更加稳健，同时避免了L2 Loss的梯度爆炸问题。
4. CrossEntropyLoss：交叉熵损失，主要应用于分类问题。

二、反向传播

反向传播（Backpropagation）是深度学习中的一种核心算法，用于计算损失函数对模型每一个参数的梯度。在优化模型参数（例如使用梯度下降算法）的过程中，我们需要知道模型每一项参数的梯度方向，以此来更新参数。

反向传播的过程可以概括为以下几个步骤：

1. 前向传播：数据沿着从输入层至输出层的方向进行传播，经过每一层的操作（如线性变换、激活函数等），最终在输出层产生预测值。
2. 损失计算：根据模型的预测值和真实值，使用损失函数计算损失。
3. 反向传播：根据链式法则（Chain Rule），从输出层开始，沿着网络的结构向反方向（输入层方向）回传，计算损失函数对每一层参数的梯度。这些梯度信息将用于后续的参数更新。
4. 参数更新：使用优化算法（如SGD、Adam等）和计算出的梯度信息更新模型中每一层的权重和偏置。通过不断迭代这个过程，模型的参数将逐渐收敛到最优解附近，从而实现对数据的准确拟合。

三、损失函数与反向传播的关系

损失函数和反向传播是紧密相关的。损失函数为反向传播提供了计算梯度的依据，而反向传播则是利用这些梯度信息来更新模型参数的过程。通过损失函数的计算和反向传播的梯度回传，我们可以不断地优化模型参数，使模型的预测结果更加接近真实标签。

# https://b23.tv/5onlMbG

16. 多元函数求导的雅克比矩阵

17.什么是梯度？

在PyTorch中，梯度（gradient）是一个非常重要的概念，主要用于反向传播算法来更新神经网络的参数。

i数学基础

- 梯度是多元函数对各个自变量的偏导数所组成的向量。在神经网络中，损失函数（如均方误差、交叉熵损失等）是关于模型参数（如权重和偏置）的函数。以一个简单的线性函数y = w*x + b为例，若要最小化预测值y与真实值之间的差异（损失函数），就需要通过调整参数w和b来实现。梯度就告诉我们在每个参数维度上，损失函数上升或者下降的速率。

j在PyTorch中的应用

- 计算梯度的步骤：

- 首先，在PyTorch中，需要设置模型的参数（例如神经网络的权重和偏置）的 requires_grad 属性为 True 。这表示需要计算这些参数的梯度。例如，对于一个简单的张量x = torch.tensor([1.0], requires_grad=True)。

- 然后，构建一个计算图，通过一系列的操作（如加法、乘法、激活函数等）得到损失函数的值。在这个过程中，PyTorch会自动记录计算图中的操作。

- 最后，调用 loss.backward() 方法，PyTorch会自动计算损失函数关于每个需要梯度的参数的梯度。这些梯度会被存储在参数的 .grad 属性中。例如，在一个简单的线性回归模型训练过程中，计算出损失后，调用 loss.backward() ，模型的权重和偏置张量的 .grad 属性就会被更新为损失函数关于它们的梯度。