XGBoost算法原理及其实现

点击下方图片查看HappyChart专业绘图软件

目标函数

$$Obj(\theta )=L(\theta )+\Omega (\theta )$$
其中，$L(\theta )$表示模型拟合训练数据的程度，$\Omega (\theta )$是正则化项，用来表示模型的复杂程度。

一般，训练集的损失函数记为：$L={\Sigma }_{i=1}^{n}l(y_i,\widehat{y_i})$

• 平方损失函数：$l(y_i,\widehat{y_i})=(y_i,\widehat{y_i}{)}^2$
• 对数损失函数：$l(y_i,\widehat{y_i})=y_{i}ln(1+e^{-\widehat{y_i}})+(1-y_i)ln(1+e^{\widehat{y_i}})$

正则化：

• L2正则化：$\Omega (\omega )=\lambda ||\omega |{|}^2$
• L1正则化：$\Omega (\omega )=\lambda ||\omega |{|}_1$

优化训练损失函数能保证模型具有预测性，而优化正则化项能是模型更简单。

回归树的集成

模型：
假设我们有K个树，则
$$\widehat{y_i}={\Sigma }_{k=1}^K{f}_k(x_i),f_k\in F$$
$F$为包含所有回归树的函数空间。
如下图：

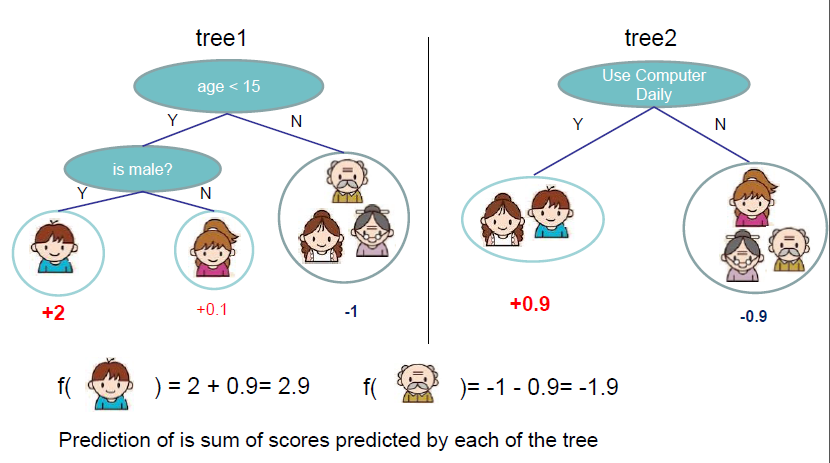
每一个人代表一个样例，而每个样例的总得分是由每个树在该样例得分加总得到的。所以$f_k(x_i)$表示在树$f_k$中样本$x_i$的得分。

学习函数

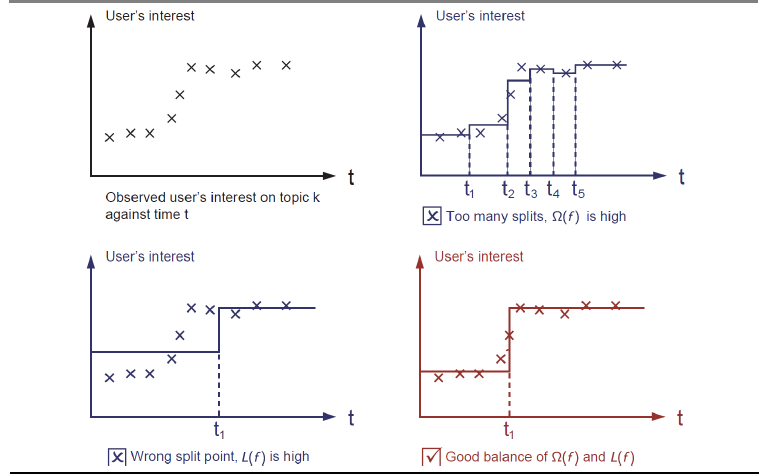
从第一张图我们看出，这是在话题k上用户兴趣随着时间的变化，在第二张图中，我们训练了一个模型，有非常多的切分点，这样虽然能很好的拟合数据，但是模型的复杂度上升了，这样可能导致大的方差；在第三张图中由于分割点错误，模型拟合不够，会造成较大的偏差，而最后一张图中在方差和偏差之间找到了较好的平衡。但是要怎样才能找到这样的平衡呢。

梯度提升

目标函数：${\Sigma }_{i=1}^{n}l(y_i,\widehat{y_i})+{\Sigma }_k\Omega (f_k),f_k\in F$
首先从一个常数预测开始，每次加一个函数：
$$\begin{gathered} {\hat{y}}_i^{(0)}=0 \\ {\hat{y}}_i^{(1)}=f_1(x_i)={\hat{y}}_i^{(0)}+f_1(x_i) \\ {\hat{y}}_i^{(2)}=f_1(x_i)+f_2(x_i)={\hat{y}}_i^{(1)}+f_2(x_i) \\ ... \\ {\hat{y}}_i^{(t)}={\Sigma }_{k=1}^t{f}_k(x_i)={\hat{y}}_i^{(t-1)}+f_t(x_i) \end{gathered}$$

在第t轮预测中${\hat{y}}_i^{(t)}={\hat{y}}_i^{(t-1)}+f_t(x_i)$，而这个$f_t(x_i)$就是在第t轮我们需要决定的。

$$\begin{gathered} Ob{j}^{(t)}={\Sigma }_{i=1}^{n}l(y_i,{\widehat{y_i}}^{(t)})+{\Sigma }_{i=1}^t\Omega (f_i) \\ ={\Sigma }_{i=1}^{n}l(y_i,{\widehat{y_i}}^{(t-1)}+f_t(x_i))+\Omega (f_t)+constant \end{gathered}$$

我们的目标就是找到$f_t$使得${\Sigma }_{i=1}^{n}l(y_i,{\widehat{y_i}}^{(t-1)}+f_t(x_i))+\Omega (f_t)$最小。
如果我们考虑平方损失函数，则
$$\begin{gathered} Ob{j}^{(t)}={\Sigma }_{i=1}^n(y_i-({\widehat{y_i}}^{(t-1)}+f_t(x_i)){)}^2+\Omega (f_t)+const \\ ={\Sigma }_{i=1}^n[2({\widehat{y_i}}^{(t-1)}-y_i)f_t(x_i)+f_t(x_i{)}^2]+\Omega (f_t)+const \end{gathered}$$
现在目标函数看起来仍非常复杂。那么，我们对目标函数进行泰勒展开式展开
二阶泰勒展开式为
$$f(x+△x)\simeq f(x)+f^{\prime }(x)△x+1/2f^{\prime \prime }(x)△x^2$$
定义：
$$g_i={\partial }_{{\hat{y}}^{(t-1)}}l(y_i,{\hat{y}}^{(t-1)}),h_i={\partial }_{{\hat{y}}^{(t-1)}}^{2}l(y_i,{\hat{y}}^{(t-1)})$$
$g_i,h_i$分别是$l(y_i,{\widehat{y_i}}^{(t-1)})$对${\hat{y}}^{(t-1)}$的一阶和二阶求导。
在这里，$f(x)=l(y_i,{\hat{y}}^{(t-1)})$，而由${\hat{y}}_i^{(t)}={\hat{y}}_i^{(t-1)}+f_t(x_i)$可知
$$△x=f_t(x_i)={\hat{y}}_i^{(t)}-{\hat{y}}_i^{(t-1)}$$
则目标函数可以写作：
$$Ob{j}^{(t)}\simeq {\Sigma }_{i=1}^n[l(y_i,{\widehat{y_i}}^{(t-1)})+g_i{f}_t(x_i)+1/2h_i{f}_t^2(x_i)]+\Omega (f_t)+const$$
当目标函数去掉常数项时为
$$Ob{j}^{(t)}\simeq {\Sigma }_{i=1}^n[g_i{f}_t(x_i)+1/2h_i{f}_t^2(x_i)]+\Omega (f_t)$$
其中$g_i={\partial }_{{\hat{y}}^{(t-1)}}l(y_i,{\hat{y}}^{(t-1)}),h_i={\partial }_{{\hat{y}}^{(t-1)}}^{2}l(y_i,{\hat{y}}^{(t-1)})$

重新定义树

f t ( x ) = w q ( x ) , w ∈ R T , q : R d → { 1 , 2 , . . . , T } f_t(x)=w_{q(x)}, w\in R^T, q:R^d\rightarrow \{1,2,...,T\} ft​(x)=wq(x)​,w∈RT,q:Rd→{1,2,...,T}
$q$代表每棵树的结构，它把一个样例映射到对应的叶结点上，$q(x)$即代表样例x在第几个叶节点上，$T$是叶结点的个数，$w_{q(x)}$为树的第$q(x)$个叶结点的权重得分

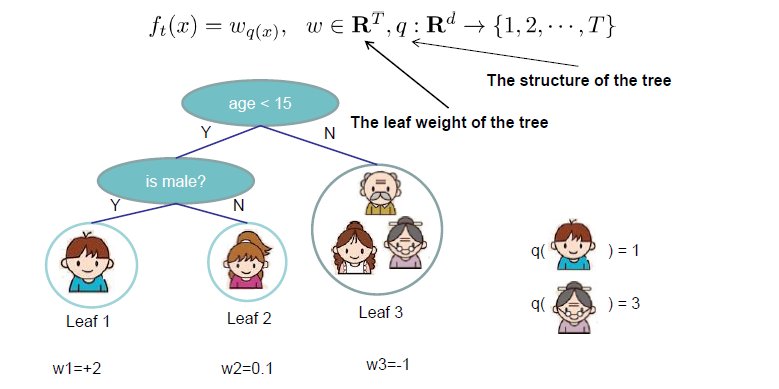
定义树的复杂度

$$\Omega =\gamma T+1/2\lambda {\Sigma }_{j=1}^T{w}_j^2$$
右边第一项$T$为叶结点的个数，第二项为L2正则化项。当然这个复杂度函数并不是唯一的。
下图展现了怎样计算复杂度

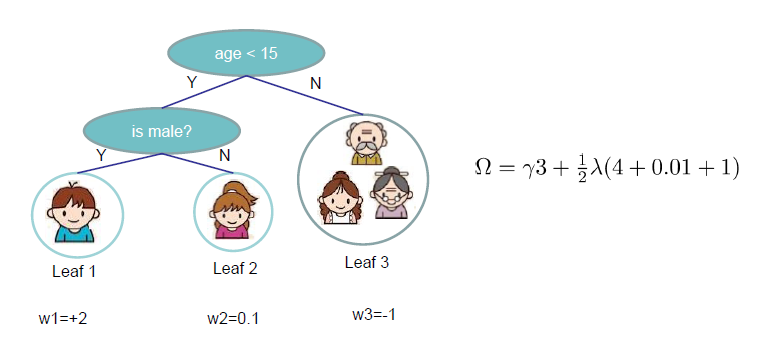
再次回顾目标函数

定义叶结点$j$的样例集为 I j = { i ∣ q ( x i ) = j } I_j=\{i|q(x_i)=j\} Ij​={i∣q(xi​)=j}

这时，目标函数为
$$\begin{gathered} Ob{j}^{(t)}\simeq {\Sigma }_{i=1}^n[g_i{f}_t(x_i)+1/2h_i{f}_i^2(x_i)]+\Omega (f_t) \\ ={\Sigma }_{i=1}^n[g_i{w}_{q(x_i)}+1/2h_i{w}_{q(x_i)}^2]+\gamma T+\lambda \frac{1}{2}{\Sigma }_{j=1}^T{w}_j^2 \\ ={\Sigma }_{j=1}^T[({\Sigma }_{i\in I_j}{g}_i)w_j+1/2({\Sigma }_{i\in I_j}{h}_i+\lambda )w_j^2]+\gamma T \end{gathered}$$
${\Sigma }_{i\in I_j}$为样例$i$在叶结点$j$的集合，而${\Sigma }_{j=1}^T$为所有的叶结点，故${\Sigma }_{i=1}^n={\Sigma }_{j=1}^T{\Sigma }_{i\in I_j}$，这样就得到最后一步了。
#结构得分及其计算
定义$G_j={\Sigma }_{i\in I_j}{g}_i,H_j={\Sigma }_{i\in I_j}{h}_i$，则
$$Ob{j}^{(t)}={\Sigma }_{j=1}^T[G_j{w}_j+1/2(H_j+\lambda )w_j^2]+\gamma T$$
假设树的结构（$q(x)$）固定，则每个叶结点的最优权重和目标函数值为：
$$w_j^{\ast }=-\frac{G_j}{H_j+\lambda },Obj=-1/2{\Sigma }_{j=1}^T\frac{G_j^2}{H_j+\lambda }+\gamma T$$
这里的目标函数可被用作得分函数，用来测量树结构q的性能。

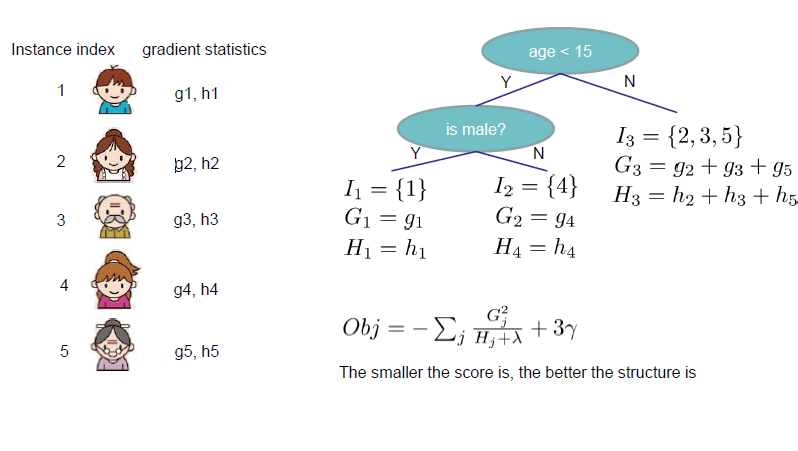
从上图，我们只需要计算一阶和二阶导数，然后加总并应用到得分方程。

树的贪婪学习

实际上，树的生长是贪婪的

• 首先从树的深度为0开始，即从根节点开始，枚举所有的特征；
• 对每一个特征，按照特征值对样例排序
• 对树的每一个叶结点，增加一个切割点，在增加切割点后，目标函数的变化为：
  $$Gain=\frac{1}{2}[\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{(G_L+G_R{)}^2}{H_L+H_R+\lambda }]-\gamma$$
  右式第一项为左子节点得分，第二项为右子节点得分，第三项为分割前的得分，$\gamma$为增加额外节点的复杂度。
• 从左向右线性扫描排序后的样例，决定最佳的特征分割节点。

时间复杂度为：$O(ndKlogn)$
对每一水平，需要$O(nlogn)$来排序，有d个特征和K个水平。

处理分类变量

xgBoost偏好处理稀疏矩阵，对于分类变量，我们需要进行one-hot编码。对分类变量进行one-hot编码后矩阵就会变得非常稀疏，这样xgBoost就容易处理。

总结

1. 每次迭代增加一颗新树
2. 开始每次迭代，计算
   $$g_i={\partial }_{{\hat{y}}^{(t-1)}}l(y_i,{\hat{y}}^{(t-1)}),h_i={\partial }_{{\hat{y}}^{(t-1)}}^{2}l(y_i,{\hat{y}}^{(t-1)})$$
3. 生成树$f_t(x)$
   $$Obj=1/2{\Sigma }_{j=1}^T\frac{G_j^2}{H_j+\lambda }+\gamma T$$
4. 把$f_t(x)$加到模型${\widehat{y_i}}^{(t)}={\widehat{y_i}}^{(t-1)}+f_t(x_i)$

• 通常我们用${\widehat{y_i}}^{(t)}={\widehat{y_i}}^{(t-1)}+ϵf_t(x_i)$代替上式
• $ϵ$称为步长，这样能防止过度拟合。

算法

R语言实现

使用的数据为kaggle竞赛的手写字体识别
注意：数据由int型必须转换为numeric，否则在训练时会出现错误，请看 stackoverflow提问的问题。

Error in xgb.DMatrix(train[, -1], label = train[, 1]) : REAL() can only be applied to a 'numeric', not a 'integer'

library(data.table)
library(caret)
library(xgboost)
digit_train <- fread("train.csv",header=T)
digit_test <- fread("test.csv",header=T)
index <- createDataPartition(digit$label,p=0.75,list=F)
train <- digit[index]
test <- digit[-index]

xgb <- xgboost(data=as.matrix(apply(digit_train[,-1],2,as.numeric)),##如果不转化为numeric，会出现上述错误
               label=as.numeric(digit_train$label),eta=0.1,nrounds=50,
               booster="gbtree",
               num_class=10,
               objective = "multi:softmax",
               max_depth = 12,
              )
pred <- predict(xgb,as.matrix(apply(digit_test,2,as.numeric)))
write.csv(pred,"pred.csv",row.names=F)

最后的精确度大约为0.95，不算好，还可以再调整参数。

CRAN上的参考文档：XGBoost R tutorial

参考文献：
Introduction to Boosted Tree
XGBoost: A Scalable Tree Boosting System
XGBoost
one-hot
XGBoost-Python完全调参指南-参数解释篇
github
XGBoost package