梯度下降法复杂度计算与公式推导
如何梯度下降法的复杂度
- 通过自己的数据进行实际代码运行测试,看看时间性能如何。但是这样子不能直观看出类似于:quick sort(nlogn)这样的复杂度
- 通过公式进行复杂度评估
Gradient Descent Algorithm
- 初始化x0∈Rdx_0\in R^dx0∈Rd 和步长 (step_size) ηt\eta_tηt>0
- for i = 1, 2, 3, …:
xi+1x_{i+1}xi+1= xix_ixi - ηt∇\eta_t\nablaηt∇f(xix_ixi)
convergence Analysis of Grandient Descent
(梯度下降法的收敛分析)
1. 定理
假设满足L- Lipschitz 条件(即是平滑函数i.e.LR等), 并且是凸函数, 设定x∗=argminf(x)x^* = argmin f(x)x∗=argminf(x)(即我们最后想得到的最优解), 步长ηt≤1L\eta_t\leq\frac{1}{L}ηt≤L1(L 即是一个常数), 即满足:
(1.1)f(xk)≤f(x∗)+∣∣x0−x∗∣∣222ηKf(x_k)\leq f(x_*) + \frac{||x_0 - x_*||_2^2}{2\eta K}\tag{1.1}f(xk)≤f(x∗)+2ηK∣∣x0−x∗∣∣22(1.1)
当我们迭代 k=L∣∣x0−x∗∣∣22εk = \frac{L||x_0 - x_*||_2^2}{\varepsilon}k=εL∣∣x0−x∗∣∣22 , 就能保证收敛到保证ε\varepsilonε - approximation optional value x(ηt=1L)x(\eta_t = \frac{1}{L})x(ηt=L1)
其中xkx_kxk是程序第K次迭代的x的值,即在程序运行中我们希望我们的f(xk)f(x_k)f(xk) 慢慢接近于f(x∗)f(x_*)f(x∗), 即 ∣∣x0−x∗∣∣222ηK\frac{||x_0 - x_*||_2^2}{2\eta K}2ηK∣∣x0−x∗∣∣22越来越小, 此时判断GD执行K值收敛的ε\varepsilonε即可知复杂度有多少。
即,将k=L∣∣x0−x∗∣∣22εk = \frac{L||x_0 - x_*||_2^2}{\varepsilon}k=εL∣∣x0−x∗∣∣22 , ηt≤1L\eta_t\leq\frac{1}{L}ηt≤L1带入(1.1):
∣∣x0−x∗∣∣222ηtL∣∣x0−x∗∣∣22ε=ε2ηtL=ε2\frac{||x_0 - x_*||_2^2}{2\eta_t \frac{L||x_0 - x_*||_2^2}{\varepsilon}} = \frac{\varepsilon}{2\eta_t L} = \frac{\varepsilon}{2}2ηtεL∣∣x0−x∗∣∣22∣∣x0−x∗∣∣22=2ηtLε=2ε
(1.2)∴f(xk)≤f(x∗)+ε2=f(x∗)+O(ε)\therefore f(x_k) \leq f(x^*) + \frac{\varepsilon}{2} = f(x^*) + O(\varepsilon) \tag{1.2}∴f(xk)≤f(x∗)+2ε=f(x∗)+O(ε)(1.2)
2. 公式求导
2.1 凸函数性质:
定义:若 f(x)f(x)f(x) 是凸函数(convexity)则任意的x,y∈Rd,0≤λ≤1x,y\in R^d, 0\leq\lambda\leq1x,y∈Rd,0≤λ≤1
(2.1)f(λx+(1−λ)y)≤λf(x)+(1−λ)f(x) f(\lambda x + (1-\lambda)y)\leq\lambda f(x) +(1-\lambda)f(x) \tag{2.1}f(λx+(1−λ)y)≤λf(x)+(1−λ)f(x)(2.1)
(2.2 . first order convexity)f(x)+∇f(x)(y−x)≤f(y) f(x) + \nabla f(x)(y-x) \leq f(y) \tag{2.2 . first order convexity}f(x)+∇f(x)(y−x)≤f(y)(2.2 . first order convexity)
2.1 L- Lipschitz2条件以及定理(给定的第二个定理):
一个光滑函数(smooth function)f 满足 L- Lipschitz条件, 则对于任意x,y∈Rd,即有x,y\in R^d, 即有x,y∈Rd,即有
(Claim 1)∣∣∇f(x)−∇f(y)∣∣≤L∣∣x−y∣∣||\nabla f(x) - \nabla f(y)|| \leq L|| x-y|| \tag{Claim 1}∣∣∇f(x)−∇f(y)∣∣≤L∣∣x−y∣∣(Claim 1)
证明Claim 1 , 举例linear regression, loss = 1n∣∣Xm−y∣∣2,Xm是矩阵形式\frac{1}{n}||X_m-y||^2,X_m是矩阵形式n1∣∣Xm−y∣∣2,Xm是矩阵形式

2.3 L- Lipschitz3条件以及定理(给定的第三个定理)
假设一个函数满足L-Lipschitz 条件, 并且是凸函数,对于任意的$x,y\in R^d, 我们有:
(2.3)f(y)≤f(x)+∇f(x)(y−x)+L2∣∣y−x∣∣2f(y)\leq f(x)+ \nabla f(x)(y-x) +\frac{L}{2} ||y-x||^2 \tag{2.3}f(y)≤f(x)+∇f(x)(y−x)+2L∣∣y−x∣∣2(2.3)
回顾积分性质:
已知: h(x):h(1)=h(0)+∫01h(τ)˙dτ h(x): h(1)= h(0) + \int_0^1\dot{h(\tau)}d\tauh(x):h(1)=h(0)+∫01h(τ)˙dτ
定义: h(τ)=f(x+τ(y−x))h(\tau)=f(x + \tau(y-x))h(τ)=f(x+τ(y−x))
所以: h(1)=f(y),h(0)=f(x)h(1)=f(y), h(0)=f(x)h(1)=f(y),h(0)=f(x)
(2.4)f(y)=f(x)+∫01∇f(x+τ(y−x))(y−x)dτf(y)=f(x)+\int_0^1\nabla f(x+\tau(y-x))(y-x)d\tau \tag{2.4}f(y)=f(x)+∫01∇f(x+τ(y−x))(y−x)dτ(2.4)
定理3 的证明:

根据上面推导的公式,证明定理1:
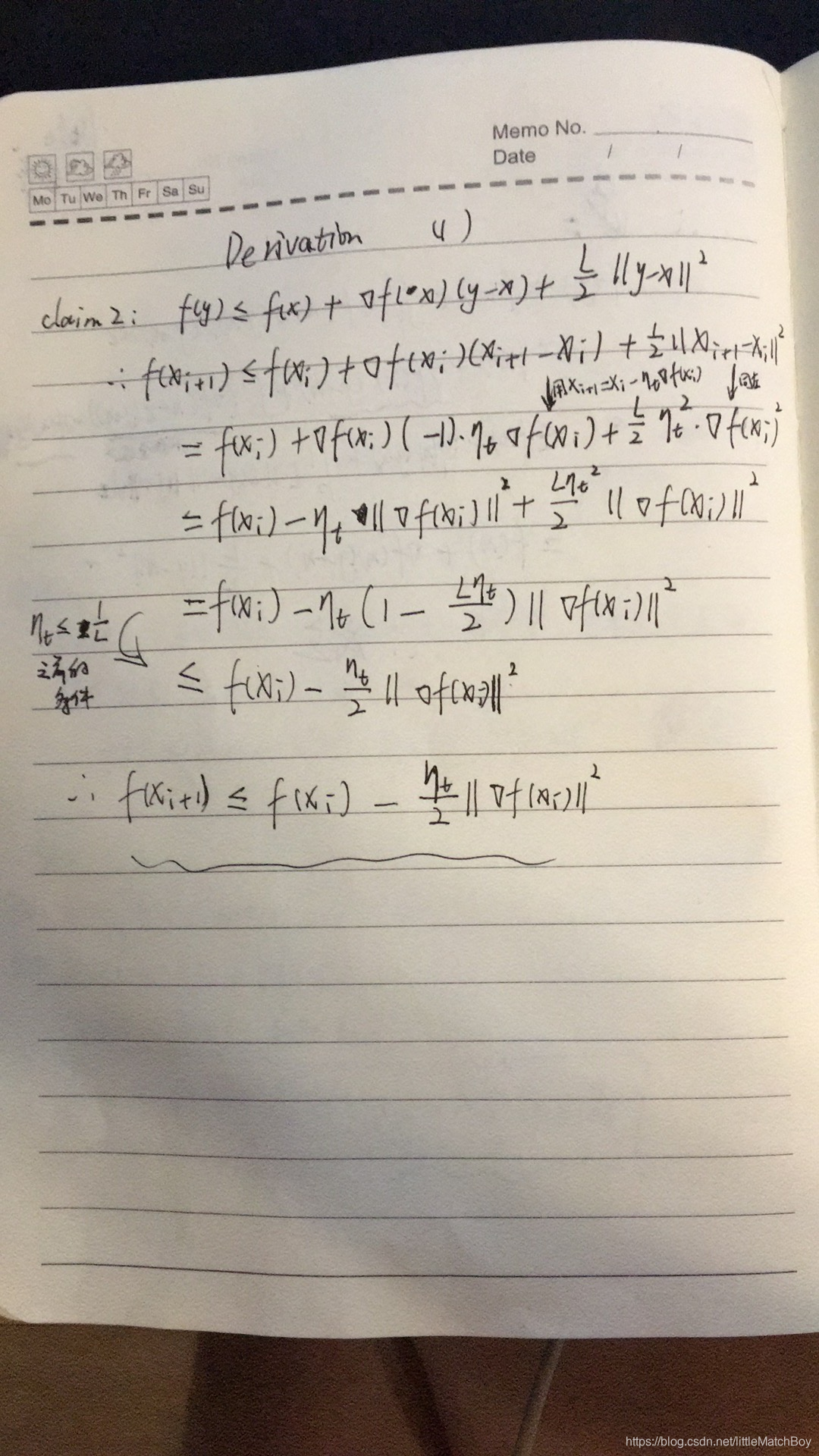


























 518
518

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








