python 最小堆最大堆

堆本质是完全二叉树，最小堆要求节点元素不大于左右叶子节点元素，最大堆要求节点元素不小于左右叶子节点元素。

下面通过例子来讲解最大堆。

给定一个列表array=[16,7,3,20,17,8]，对其进行堆排序。首先根据该数组元素构建一个完全二叉树，得到

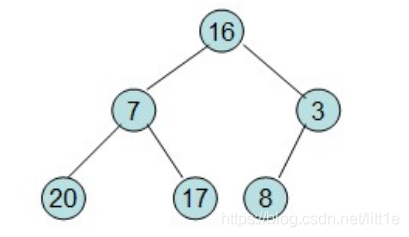
根据最大堆的定义要求，我们需要让节点元素不小于左右叶子节点元素，所以我们从最后一个非叶节点开始依次向上调整元素位置。
构造初始堆，则从最后一个非叶节点开始调整，调整过程如下：
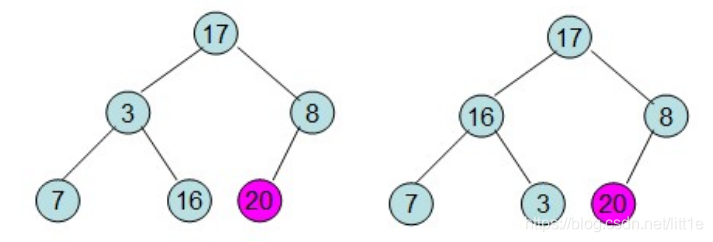
第一步: 初始化大顶堆(从最后一个有子节点开始往上调整最大堆)

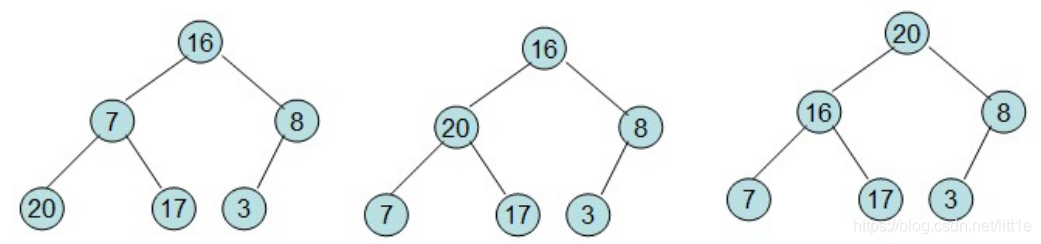
20和16交换后导致16不满足堆的性质，因此需重新调整

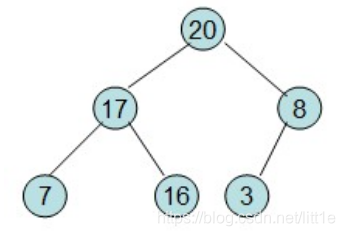
这就得到了初始堆。

第二步: 堆顶元素R[1]与最后一个元素R[n]交换，交换后堆长度减一

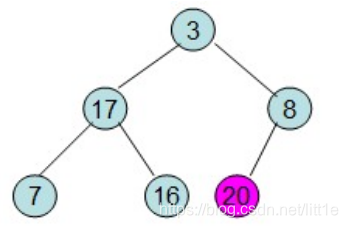
第三步: 重新调整堆。此时3位于堆顶不满堆的性质，则需调整继续调整(从顶点开始往下调整)

重复上面的步骤:

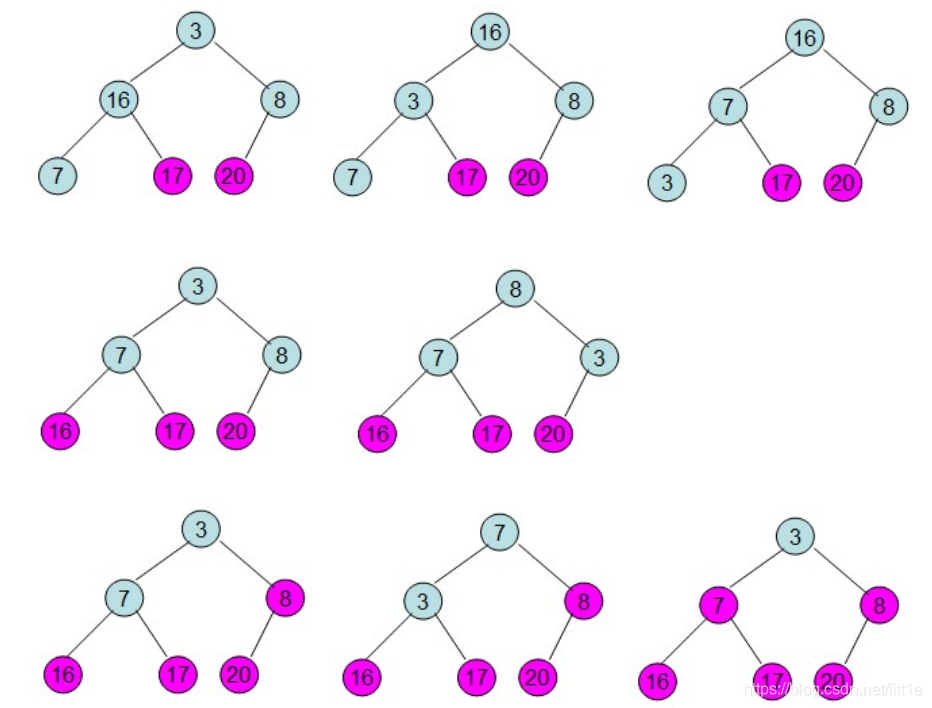
请特别特别注意: 初始化大顶堆时 是从最后一个有子节点开始往上调整最大堆。而堆顶元素(最大数)与堆最后一个数交换后，需再次调整成大顶堆，此时是从上往下调整的。

class Solution:
    def max_heapify(self, heap, root, heap_len