计算机视觉-利用霍夫变换检测直线

霍夫变换（Hough Transform）是一种用于检测图像中特定形状（如直线、圆等）的经典算法，其检测直线的原理如下：

直线的参数表示

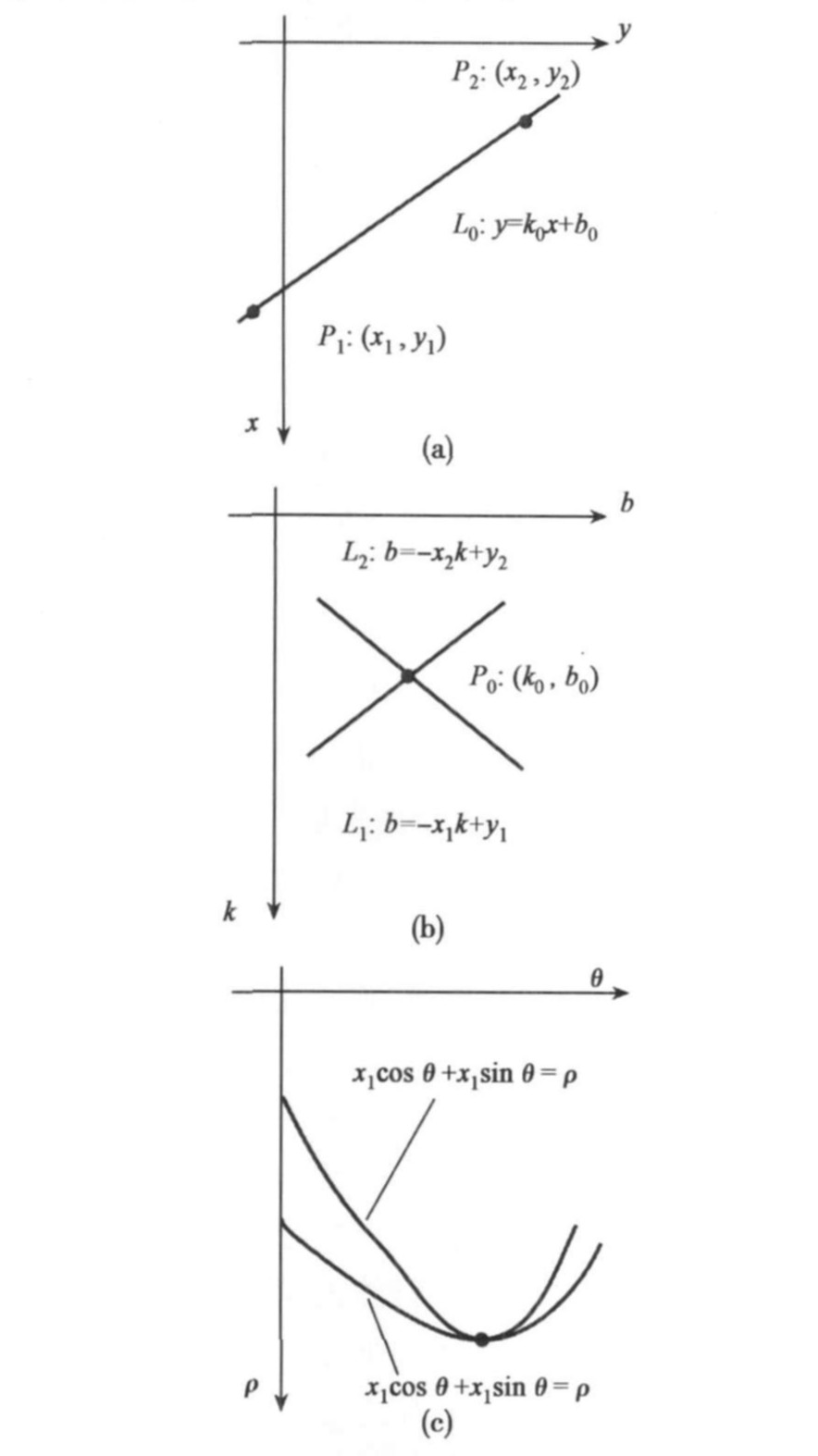
在笛卡尔坐标系中，直线可以用方程\(y = kx + b\)来表示，其中k是斜率，b是截距。但这种表示方法存在一些问题，例如当直线垂直于x轴时，斜率k会趋于无穷大，导致数值计算上的困难。

为了避免这个问题，在霍夫变换中通常使用极坐标来表示直线。对于平面上的任意一点\((x,y)\)，从原点到该点的向量可以用极坐标\((\rho,\theta)\)来表示，其中\(\rho\)是向量的长度，\(\theta\)是向量与x轴正方向的夹角。那么，直线在极坐标下的方程可以表示为\(\rho = x\cos\theta + y\sin\theta\)。

霍夫空间与投票机制

• 霍夫空间：对于图像中的每一个点\((x,y)\)，将其代入极坐标方程\(\rho = x\cos\theta + y\sin\theta\)，可以得到一系列的\((\rho,\theta)\)组合，这些组合构成了该点在霍夫空间中的一条曲线。实际上，图像中同一条直线上的所有点，在霍夫空间中对应的曲线会相交于一点，这个交点的坐标\((\rho,\theta)\)就代表了图像中的这条直线。
• 投票机制：为了找到图像中的直线，需要在霍夫空间中进行 “投票”。首先创建一个二维数组作为霍夫累加器，其维度通常根据\(\rho\)和\(\theta\)的取值范围来确定。对于图像中的每一个边缘点（通过边缘检测算法得到），在霍夫空间中计算其对应的\((\rho,\theta)\)曲线，并在累加器中相应的位置进行投票（通常是将该位置的数值加 1）。投票结束后，累加器中数值较高的点就对应着图像中可能存在的直线。

阈值处理与峰值检测

• 阈值处理：为了确定哪些点是真正的直线，需要设置一个阈值。只有当累加器中的某个点的投票数超过阈值时，才认为该点对应着图像中的一条直线。
• 峰值检测：在超过阈值的点中，通常还需要进行峰值检测，以找到真正的直线参数。这是因为可能存在一些相邻的点都超过了阈值，但它们实际上代表的是同一条直线。通过峰值检测算法（如非极大值抑制等），可以找到霍夫空间中的局部最大值，这些最大值对应的\((\rho,\theta)\)就是最终检测到的直线的参数。

霍夫变换（Hough Transform）是一种用于检测图像中特定形状（如直线、圆等）的经典算法，其检测直线的原理如下：

直线的参数表示

在笛卡尔坐标系中，直线可以用方程\(y = kx + b\)来表示，其中k是斜率，b是截距。但这种表示方法存在一些问题，例如当直线垂直于x轴时，斜率k会趋于无穷大，导致数值计算上的困难。

为了避免这个问题，在霍夫变换中通常使用极坐标来表示直线。对于平面上的任意一点\((x,y)\)，从原点到该点的向量可以用极坐标\((\rho,\theta)\)来表示，其中\(\rho\)是向量的长度，\(\theta\)是向量与x轴