问题如下: leetcode 587
在一个二维的花园中,有一些用 (x,y) 坐标表示的树。由于安装费用十分昂贵,你的任务是先用最短的绳子围起所有的树。只有当所有的树都被绳子包围时,花园才能围好栅栏。你需要找到正好位于栅栏边界上的树的坐标。
解法一:暴力解法
我们知道凸包的性质,凸包一定是【最外围】的那些点圈成,所以假设有n个点,那么最多可以构造出n(n−1)2条边,算法如下:
1. 选定一条边,遍历其他n-2个点,如果所有点都在该条边的一侧,则加入凸包集合。
2. 不断重复步骤1,直到所有边都被遍历过。
如何判断一个点 p3 是在直线 p1p2 的左边还是右边呢?(坐标:p1(x1,y1),p2(x2,y2),p3(x3,y3))我们可以计算: 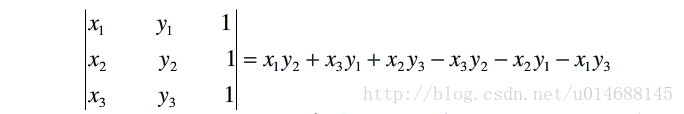
当上式结果为正时,p3在直线 p1p2 的左侧;当结果为负时,p3在直线 p1p2 的右边。
#include <iostream>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <unordered_set>
#include <set>
#include <vector>
#include <map>
#include <set>
#include <queue>
#include <string>
using namespace std;
int calcuTriangle(int x1, int y1, int x2, int y2, int x3, int y3)
{
return x1 * y2 + x3 * y1 + x2 * y3 - x3 * y2 - x2 * y1 - x1 * y3;
}
//O(n^3)
set<vector<int>> tubao_baoli(vector<vector<int>>& tree)
{
set<vector<int>> ret;
if (tree.size() <= 1)
return ret;
for (int i = 0; i < tree.size(); i++)
{
for (int j = i + 1; j < tree.size(); j++)
{
int onesize = 0, othersize = 0;
for (int k = 0; k < tree.size(); k++)
{
if (k == i || k == j)
continue;
int tmp = calcuTriangle(tree[i][0], tree[i][1], tree[j][0], tree[j][1], tree[k][0], tree[k][1]);
if (tmp > 0)
onesize ++;
else if (tmp < 0)
othersize ++;
}
if ( onesize == 0 || othersize == 0) //如果某一边没有点,当前两个点都是凸点
{
ret.insert(vector<int> {tree[i][0], tree[i][1]});
ret.insert(vector<int> {tree[j][0], tree[j][1]});
}
}
}
return ret;
}
int main()
{
int n = 5;
vector<vector<int>> trees{{1,1},{2,0},{4,2},{3,3},{2,2},{2,4}};
set<vector<int>> ret = tubao_baoli(trees);
for (auto it : ret)
cout<<it[0]<<" "<<it[1]<<endl;
return 0;
}
解法二:Graham扫描法
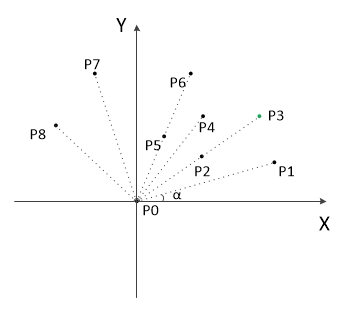
第一步:找y最小的点(如果相等就找其中x最小的)作为基准点P0。
第二步:把所有点的坐标平移一下,使 P0 作为原点,如上图。
第三步:计算各个点相对于 P0 的幅角 α (弧度),按从小到大的顺序对各个点排序。
当 α 相同时,分条件考虑:
如果当前弧度是最大弧度,说明在最左边边界,距离 P0 比较远的排在前面。
如果当前弧度是最小弧度,说明在最右边边界,距离 P0 比较近的排在前面。
如果在中间,那就都可以。
例如上图得到的结果为 P1,P2,P3,P4,P5,P6,P7,P8。我们由几何知识可以知道,结果中第一个点 P1 和最后一 个点 P8 一定是凸包上的点。
第四步:我们已经知道了凸包上的第一个点 P0 和第二个点 P1,我们把它们放在栈里面。现在从步骤3求得的那个结果里,把 P1 后面的所有点拿出来做当前点,遍历进行第五步。
第五步:连接栈顶的第二个点和栈顶的那个点,得到直线 L 。
看当前点是在直线 L 的右边还是左边。
如果在直线的右边就说明现在栈顶的点不是凸点,将栈顶的点弹出。当前点不变。
如果在直线上,或者在直线的左边,说明当前栈顶的点是满足条件的,把当前点入栈。遍历后一个点。
第六步:当把步骤3求得的结果里的所有点都遍历完了,还剩在栈里面的点就是凸点。导出即可。
代码如下:
#include <iostream>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <unordered_set>
#include <set>
#include <vector>
#include <map>
#include <set>
#include <queue>
#include <stack>
#include <string>
#include <math.h>
using namespace std;
struct Point {
int x;
int y;
Point() : x(0), y(0) {}
Point(int a, int b) : x(a), y(b) {}
};
class MYPoint{
public:
MYPoint(int a, int b, double c):x(a), y(b),hudu(c){}
int x;
int y;
double hudu;
static double maxHuDu;
bool operator<(const MYPoint& b) const
{
if (this->hudu == b.hudu)
{
if (this->hudu == maxHuDu) //说明是左侧的边界。从远到近
return (pow(this->x, 2) + pow(this->y, 2)) > (pow(b.x, 2) + pow(b.y, 2));
else //如果是右侧边界,从近到远。如果不是边界,都可以(也使用从近到远)
return (pow(this->x, 2) + pow(this->y, 2)) < (pow(b.x, 2) + pow(b.y, 2));
}
return this->hudu < b.hudu;
}
};
double MYPoint::maxHuDu = INT_MIN;
class Solution {
public:
vector<Point> outerTrees(vector<Point>& points)
{
if (points.size() <= 3)
return points;
//首先找P0点(y最小的点)
int minY = INT_MAX, minYpos;
for (int i = 0; i < points.size(); i++)
{
if (points[i].y < minY)
{
minY = points[i].y;
minYpos = i;
}
else if (points[i].y == minY && points[i].x < points[minYpos].x)
{
minY = points[i].y;
minYpos = i;
}
}
//cout<<"标准点:"<<points[minYpos].x<<"-"<<points[minYpos].y<<endl;
vector<Point> ret; //返回的凸点
vector<MYPoint> mypoints;
for (int i = 0; i < points.size(); i++)
{
if (i == minYpos)
continue;
double yy = points[i].y - points[minYpos].y, xx = points[i].x - points[minYpos].x;
double hudu = atan2(yy, xx);
MYPoint::maxHuDu = dou_max(MYPoint::maxHuDu, hudu); //要把最大弧度存下来。之后排序的一个关键点!
mypoints.push_back(MYPoint(points[i].x - points[minYpos].x, points[i].y - points[minYpos].y, hudu)); //存的是相对位置。最后要补偿回来。
}
sort(mypoints.begin(), mypoints.end());
// int jishu = 1;
// for (auto it : mypoints)
// cout<<"P"<<jishu++<<" "<<it.x<<" "<<it.y<<" "<<it.hudu<<endl;
//第二个步骤
vector<MYPoint> stk;
stk.push_back(MYPoint(0, 0, 0)); //压入P0(坐标[0,0])
stk.push_back(mypoints[0]); //压入P1
for (int i = 1; i < mypoints.size(); i++)
{
//如果在左边或者在线上 就入栈
if (calcuTriangle(stk[stk.size() - 2].x, stk[stk.size() - 2].y, stk.back().x, stk.back().y, mypoints[i].x, mypoints[i].y))
{
stk.push_back(mypoints[i]);
//cout<<"P"<<i + 1 << " "<<mypoints[i].x<<" "<<mypoints[i].y<<" 满足"<<endl<<endl;
}
else //否则,弹出栈顶
{
stk.pop_back();
//cout<<"P"<<i + 1 << " "<<mypoints[i].x<<" "<<mypoints[i].y<<" 不满足"<<endl<<endl;
i--; //当前点下一轮还是作为判断点
}
}
cout<<endl;
//最后,栈内剩下的都是凸点
for (auto it : stk)
ret.push_back(Point(it.x + points[minYpos].x, it.y + points[minYpos].y)); //之前都是算的相对位置。最后返回要加上来。
return ret;
}
bool calcuTriangle(int x1, int y1, int x2, int y2, int x3, int y3)
{
//cout<<x1<<" "<<y1<<" "<<x2<<" "<<y2<<" "<<x3<<" "<<y3<<endl;
return x1 * y2 + x3 * y1 + x2 * y3 - x3 * y2 - x2 * y1 - x1 * y3 >= 0; //判断是否在左边
}
double dou_max(double a, double b)
{
return (a > b) ? a : b;
}
};
int main()
{
//vector<vector<int>> trees{{1,1},{2,0},{4,2},{3,3},{2,2},{2,4}};
//vector<vector<int>> trees{{3,0},{4,0},{5,0},{6,1},{7,2},{7,3},{7,4},{6,5},{5,5},{4,5},{3,5},{2,5},{1,4},{1,3},{1,2},{2,1},{4,2},{0,3}};
//vector<vector<int>> trees{{0,0},{0,1},{0,2},{1,2},{2,2},{3,2},{3,1},{3,0},{2,0}};
//vector<vector<int>> trees{{0,2},{0,4},{0,5},{0,9},{2,1},{2,2},{2,3},{2,5},{3,1},{3,2},{3,6},{3,9},{4,2},{4,5},{5,8},{5,9},{6,3},{7,9},{8,1},{8,2},{8,5},{8,7},{9,0},{9,1},{9,6}};
vector<vector<int>> trees{{1,0},{0,0},{2,0},{3,0}};
vector<Point> points;
for (int i = 0; i < trees.size(); i++)
points.push_back(Point(trees[i][0], trees[i][1]));
vector<Point> ret = Solution().outerTrees(points);
for (auto it : ret)
cout<<it.x<<" "<<it.y<<endl;
return 0;
}
关于leetcode 587的问题:
上面的代码跑587在
[[0,0],[0,1],[0,2],[1,2],[2,2],[3,2],[3,1],[3,0],[2,0]] 会报错。
但是单独调试这个实例又是正确的答案。所以很困惑。






















 366
366

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








