实验目的:
(1)了解6174猜想的内容。
(2)熟练使用选择结构和循环结构。
(3)了解标准库itertools中combinations函数的用法。
(4)熟练使用字符串的join()方法。
(5)熟练使用内置函数int()、str()、sorted()。
实验内容:
1955年,卡普耶卡(D.R.Kaprekar)对4位数字进行了研究,发现一个规律:对任意各位数字不相同的4位数,使用各位数字能组成的最大数减去能组成的最小数,对得到的差重复这个操作,最终会得到6174这个数字,并且这个操作最多不会超过7次。
编写程序,适用枚举法对这个猜想进行验证。
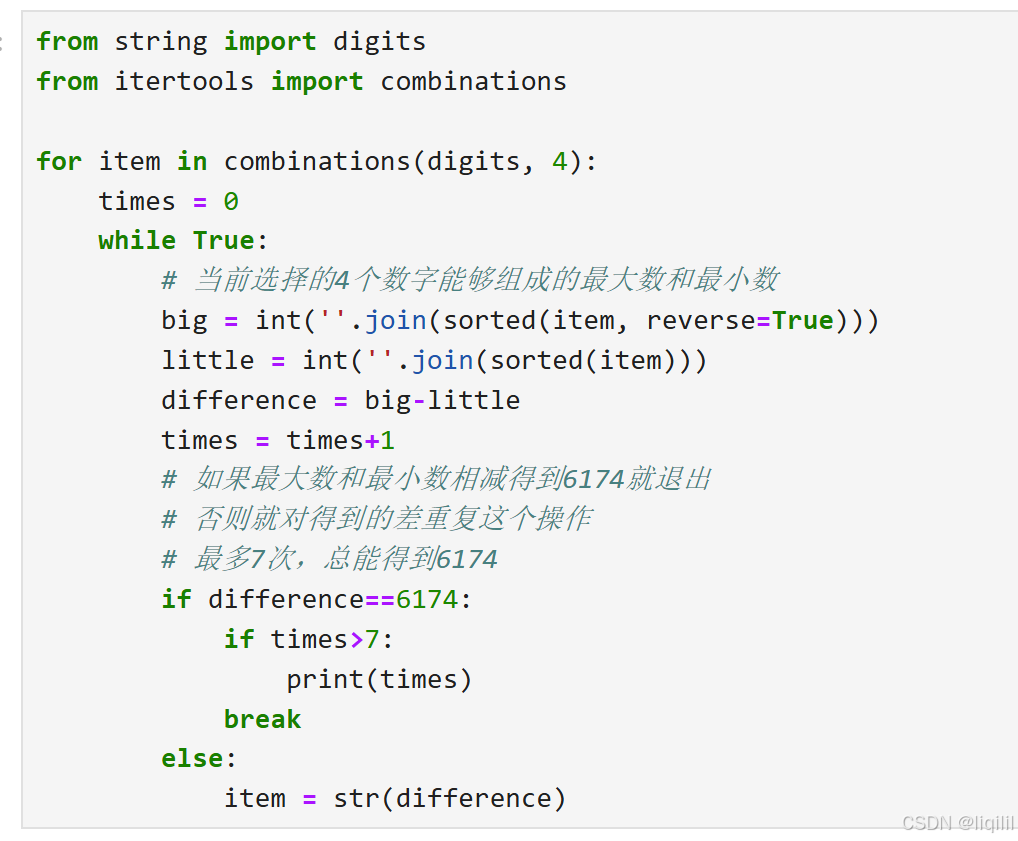
这串代码实现了一个被称为卡普雷卡尔常数(Kaprekar’s constant)6174的算法。下面是代码的逐步解释:
-
from string import digits:这一行代码从Python的string模块中导入digits,这是一个包含所有单个数字字符的字符串,即’0123456789’。 -
from itertools import combinations:这一行代码从itertools模块中导入combinations函数,该函数用于生成给定长度的所有可能的组合。 -
for item in combinations(digits, 4)::这行代码创建了一个循环,它遍历由digits中4个数字组成的所有可能组合。注意,这里不会产生包含前导零的组合,因为combinations默认会按照输入序列的顺序生成组合。 -
times = 0:初始化一个计数器,用来记录操作次数。 -
while True::开始一个无限循环,直到遇到break语句才会退出。 -
big = int(''.join(sorted(item, reverse=True))):将当前的4个数字组合按降序排序,并转换成整数,得到最大数。 -
little = int(''.join(sorted(item))):将当前的4个数字组合按升序排序,并转换成整数,得到最小数。 -
difference = big - little:计算最大数和最小数的差。 -
times = times + 1:每进行一次操作,计数器加一。 -
if difference == 6174::检查得到的差是否为6174,如果是,则执行以下操作。 -
if times > 7::如果操作次数大于7,打印操作次数(尽管卡普雷卡尔常数的性质保证了任何4位数的操作都不会超过7次)。 -
break:退出循环。 -
else::如果得到的差不是6174,则执行以下操作。 -
item = str(difference):将差值转换回字符串,并用它替换当前的数字组合,然后循环回到开始,重复这个过程。
这个过程最终总是会在7次操作以内得到6174,这就是卡普雷卡尔常数的神奇之处。代码中打印操作次数的部分似乎有些多余,因为根据卡普雷卡尔常数的性质,这个数总是会在7次以内得到,所以理论上不会打印任何东西。如果想要验证这一点,可以将打印语句保留在代码中。
实验结果:
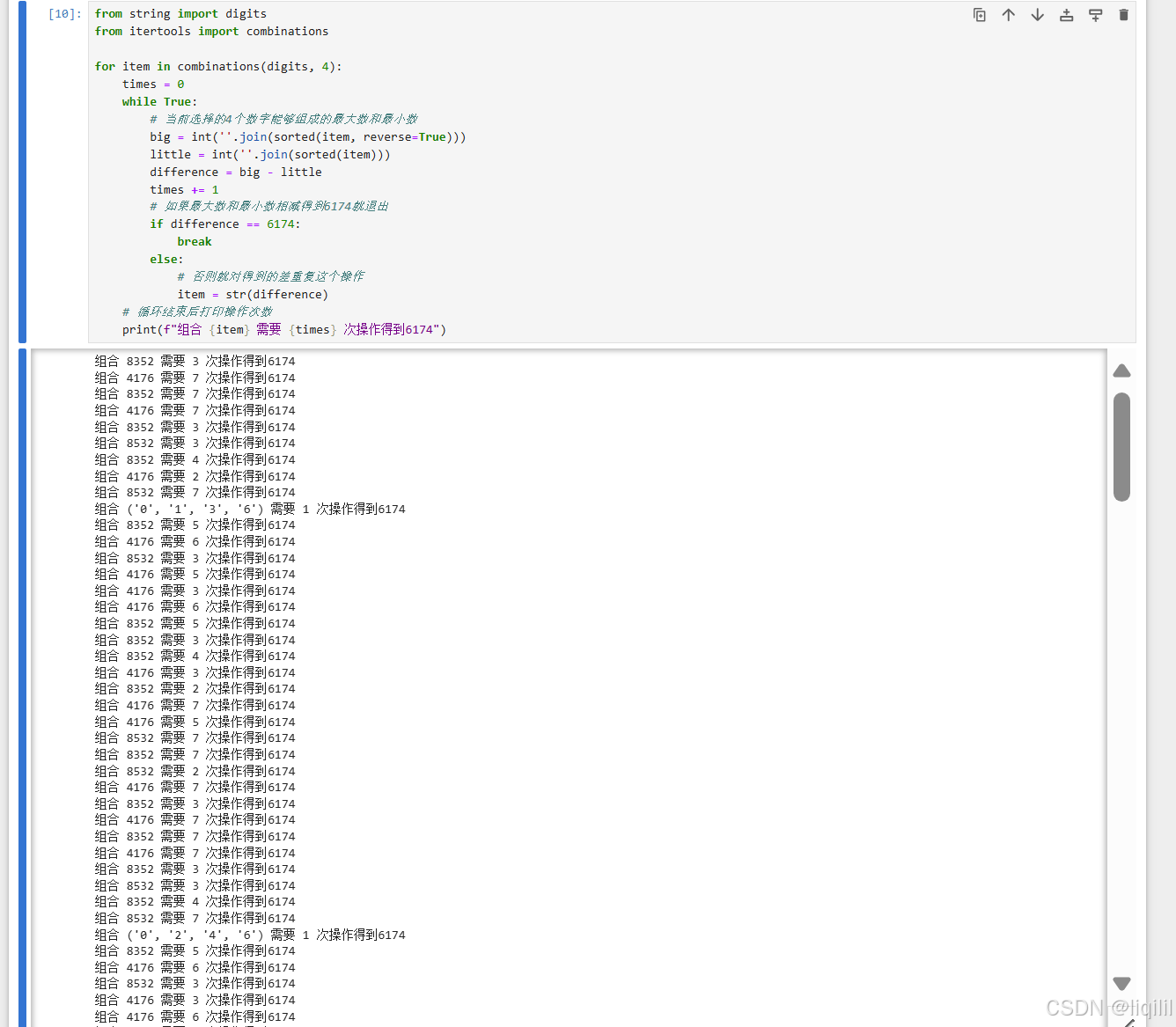




















 2819
2819

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








