第一章、基础算法
排序(掌握sort的用法,如重新调整排序规则)
- 算法描述及代码:
sort是排序的一种,它可以从小到大进行排序
sort(a+1,a+n+1);
n是需要排序的个数
- 算法案例及拓展:
案例:
输入5个数,分别是1,3,2,4,5,将它们进行排序;
sort(a+1,a+n+1);
另外 ,我们可以在sort里面加入条件,比如:从大到小进行排序;
struct node{
int x;
}a[N];
bool cmp(node a,node b)
{
if(a.x>b.x)return a.x>b.x;
}
sort(a+1,a+n+1,cmp);
二分
整数二分

区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用:符合条件的第一个位置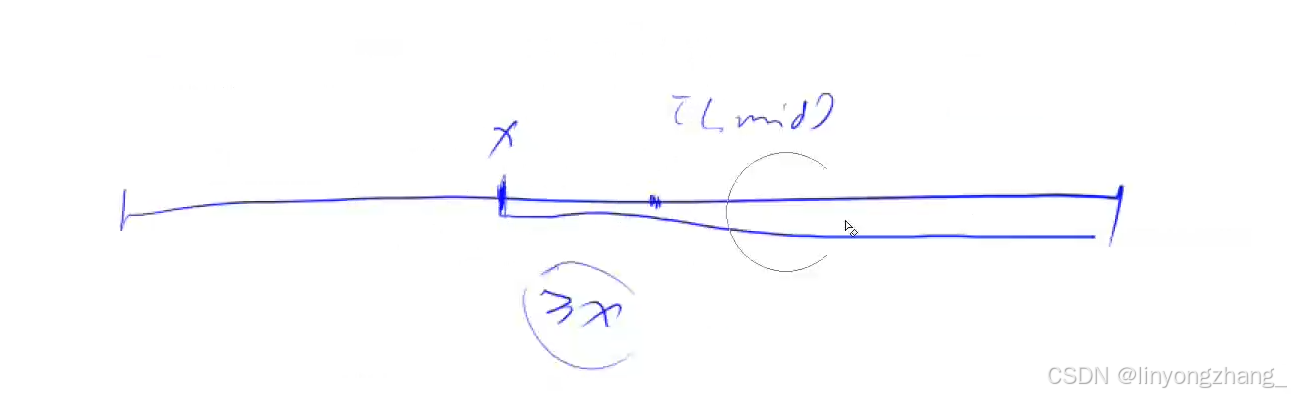
区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用:符合条件的最后一个位置
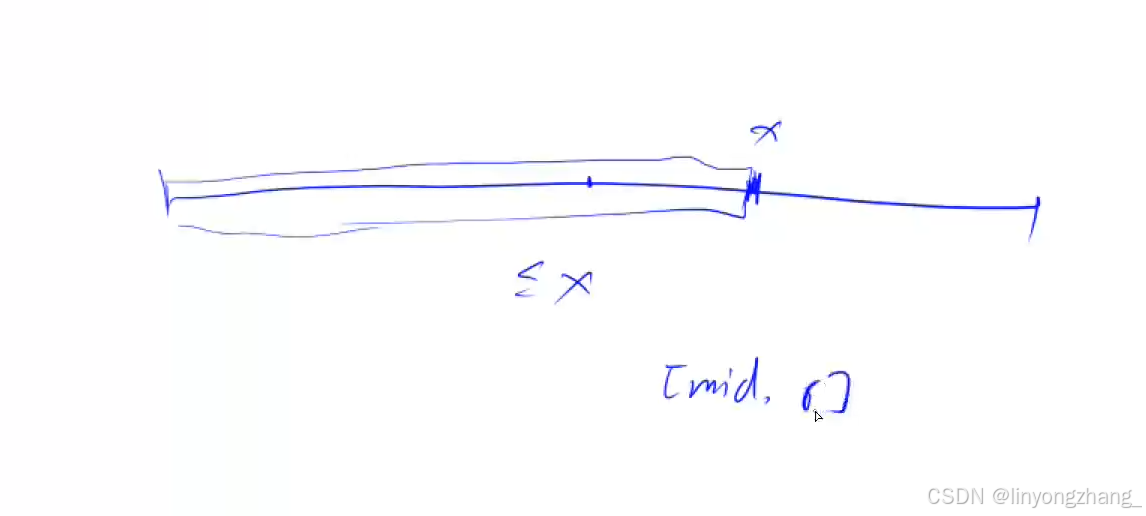
//区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用:符合条件的第一个位置
while (l < r){
int mid = l + r >> 1;
if (check(mid)) r = mid; // check(mid) 判断 [l,mid] 这个区间是否满足条件
else l = mid + 1;
}
// 此时l==r
return l;
---------------------------------------------------------------
//区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用:符合条件的最后一个位置
while (l < r){
int mid = l + r + 1 >> 1; // + 1 的原因是 l + r >> 1 == l, l = mid 这条就会导致死循环
if (check(mid)) l = mid; // check(mid) 判断 [mid,r] 这个区间是否满足条件
else r = mid - 1;
}
// 此时l==r
return l;
浮点数二分
double bs(double l, double r){
const double eps = 1e-6; // 查找的精度
while (r - l > eps){
double mid = (l + r) / 2;
if (check(mid)) r = mid;
else l = mid;
}
return l;
}
高精度(学习使用Python中的高精度)
加法:
a = 1234567890123456789
b = 9876543210987654321
c = a + b
print(c) # 输出 11111111101111111110
减法
a = 1234567890123456789
b = 9876543210987654321
c = a - b
print(c) # 输出 -8641973208631975392
乘法
a = 1234567890123456789
b = 9876543210987654321
c = a * b
print(c) # 输出 12193263113702179553906420029227418949
除法
a = 1234567890123456789
b = 9876543210987654321
c = a // b # 整除
d = a % b # 取余
print(c, d) # 输出 1 246913580123456790
如果数非常大,可以用Decimal,因为它的精度非常高
整数
from decimal import Decimal
a=Decimal('12345678978799945')
b=Decimal('13548635799741354')
c=a+b
print(c);
小数
from decimal import Decimal,getcontext
getcontext().prec=50
a=Decimal('0.1')
b=Decimal('0.2')
c=a+b
print(c);
getcontext().prec是设置精度
前缀和与差分
- 算法描述及代码:
一维前缀和
for(int i=1;i<=n;i++)s[i]=s[i-1]+a[i];
while(m--)
{
int l,r;
cin>>l>>r;
cout<<s[r]-s[l-1];
}
二维前缀和
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
f[i][j] = f[i-1][j]+f[i][j-1]-f[i-1][j-1]+a[i][j];
}
}
----------------------------------------------------------------------
while(q--)
{
int x1,y1,x2,y2;
// cin>>x1>>y1>>x2>>y2;
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
cout<<s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1]<<endl;
}
一维差分
void in(int l,int r,int c)
{
b[l]+=c;
b[r+1]-=c;
}
----------------------------------------------------------------------
for(int i=1;i<=n;i++)
{
in(i,i,a[i]);
}
----------------------------------------------------------------------
while(m--)
{
cin>>l>>r>>c;
in(l,r,c);
}
二维差分
void sd(int x1,int y1,int x2,int y2,int c)
{
b[x1][y1]+=c;
b[x2+1][y1]-=c;
b[x1][y2+1]-=c;
b[x2+1][y2+1]+=c;
}
----------------------------------------------------------------------
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
sd(i,j,i,j,a[i][j]);
}
}
----------------------------------------------------------------------
while(q--)
{
int x1,y1,x2,y2,c;
cin>>x1>>y1>>x2>>y2>>c;
sd(x1,y1,x2,y2,c);
}
- 算法案例及拓展:
双指针算法(一般掌握)
//双指针:指的是在遍历元素的过程中,不是使用单个指针进行访问,而是使用两个指针进行访问,从而达到相应的目的
//模板
for (int i = 0, j = 0; i < n; i ++ )
{
while (j < i && check(i, j)) j ++ ;
// 具体问题的逻辑
}
位运算(会用常用即可)
int lowbit(int x)
{
return x&-x;
}
int main(){
int n;
cin >> n;
while(n--)
{
int x, s = 0;
cin >> x;
for(int i = x; i; i -= lowbit(i)) s++;
cout<< s <<" ";
}
}
离散化(会用模板就行)
int a[N];//存储坐标插入的值
int s[N];//存储数组a的前缀和
vector<int> alls; //存储(所有与插入和查询有关的)坐标
vector<pair<int, int>> add, query; //存储插入和询问操作的数据
int find(int x) { //返回的是输入的坐标的离散化下标
int l = 0, r = alls.size() - 1;
while (l < r) {
int mid = l + r >> 1;
if (alls[mid] >= x) r = mid;
else l = mid + 1;
}
return r + 1;
}
---------------------------------------------------------------
//排序,去重
sort(alls.begin(), alls.end());
alls.erase(unique(alls.begin(), alls.end()), alls.end());
//执行前n次插入操作
for (auto item : add) {
int x = find(item.first);
a[x] += item.second;
}
//前缀和
for (int i = 1; i <= alls.size(); i++) s[i] = s[i-1] + a[i];
//处理后m次询问操作
for (auto item : query) {
int l = find(item.first);
int r = find(item.second);
cout<<s[r]-s[l-1]<<endl;
}
区间合并(能够掌握经典案例就行)
struct node {
int l,r;
};
node s[100010],ss[100010];
bool cmp(node a,node b){
if (a.l != b.l) return a.l < b.l;
return a.r < b.r;
}
---------------------------------------------------------------------
int n;
cin >> n;
for (int i = 0; i < n; i ++){
cin >> s[i].l >> s[i].r;
}
sort(s,s+n,cmp);
int ans = 0,st = -2e9,ed = -2e9;
for (int i = 0; i < n; i ++){
if (ed < s[i].l){
if (i != 0){
// 需要存区间的话
}
ans ++;
st = s[i].l;
ed = s[i].r;
}else{
ed = max(ed,s[i].r);
}
}
cout << ans << endl;
第二章、数据结构
链表与邻接表:树与图的存储(重点掌握)
int h[N],e[N],ne[N],idx;
//存储k所有可以走到的点,h[k]存储这个单链表的头结点
---------------------------------------------------------------
void add(int a,int b){
e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}//添加一条边a->b
---------------------------------------------------------------
idx=0;//初始化
memset(h,-1,sizeof(h));
栈与队列:单调队列、单调栈(最后在学,目前不要求)
并查集(最后在学,目前不要求)
int find(int x)
{
if(p[x]!=x) p[x]=find(p[x]);
/*
每个集合中只有祖宗节点的p[x]值等于他自己,即:
p[x]=x;
*/
return p[x];
//找到了便返回祖宗节点的值
}
---------------------------------------------------------------
if(*op=='M') p[find(a)]=find(b);//集合合并操作;
if(find(a)==find(b)) cout<<Yes<<endl;//如果祖宗节点一样,就输出yes
堆(重点掌握:会使用C++STL库中的priority_queue就行)
stack<int>y;//栈
map<char,int>mp;
priority_queue<int>h;//自动排序大到小,堆
priority_queue<int,vector<int>,greater<int>>l;
---------------------------------------------------------------
cin>>n>>m;
for(int i=1;i<=n;i++){
int t;
cin>>t;
l.push(t);
}
while(m--){
cout<<l.top()<<" ";
l.pop();
}
Hash表(会使用模板就行)
typedef unsigned long long ull;
ull h[N],p[N];//h[k]存储字符串前k个字母的哈希值, p[k]存储 P^k mod 2^64
char a[N];
set<ull>se;
---------------------------------------------------------------
ull get(int l,int r)
{
return h[r]-h[l-1]*p[r-l+1];
}
---------------------------------------------------------------
cin>>a+1;
n=strlen(a+1);
p[0]=1;//初始化
for(int i=1;i<=n;i++)
{
h[i]=h[i-1]*P+a[i];
p[i]=p[i-1]*P;
}
se.insert(get(1,n));
---------------------------------------------------------------
cout<<se.size();
第三章、搜索与图论
DFS与BFS(重点掌握)
DFS
void dfs(int u ) // 第几个数字,一共几个数字
{
if(u == n)// 递归到最后一个数字
{
for (int i = 0; i < n; i ++ ) cout << path[i] << ' '; // 输出保存的结果
puts(" ");
}
for (int i = 1; i <= n; i ++ )
if (!st[i]) // 没有被用过的数
{
path[u] = i ;
st[i] = true; // i被用过
dfs(u + 1);// 走到下一层
st[i] = false;// 恢复现场
}
}
BFS
int bfs()
{
memset(d,-1,sizeof d); //将d数组所有元素初始化为-1
d[0][0]=0; //位于原点时到原点的距离为0
q.push({0,0}); //将原点入队
int dx[4]={-1,0,1,0},dy[4]={0,1,0,-1}; //定义方向向量一共四个方向
while(q.size()) //当队列非空时执行循环
{
auto t=q.front();
q.pop(); //插入一个位置的同时会弹出一个位置保证循环可以正常终止
for(int i=0;i<4;i++) //x,y都要四个方向,遍历四个方向
{
int x=t.first+dx[i],y=t.second+dy[i]; //四个方向对应x,y坐标
if(x>=0 && x<n && y<m && y>=0 && g[x][y]==0 && d[x][y]==-1 )
{
d[x][y]=d[t.first][t.second]+1; //走到下一个点的同时距离加1
q.push({x,y}); //将该点入队
}
}
}
return d[n-1][m-1]; //递归回下一个点
}
树与图的遍历:拓扑排序(会解决一般案例就行)
void topsort() // 过程类似bfs
{
queue<int> q;
for (int i = 1; i <= n; i ++ )
if (d[i] == 0) q.push(i); // 入度为0即入队
while (q.size())
{
auto t = q.front(); cout << t << " ";
q.pop();
for (auto v : g[t])
{
if (-- d[v] == 0) // 入度为0即入队
{
q.push(v);
}
}
}
}
最短路
dijkstra
int n,m;
int g[N][N];//g[ 1 ][ 2 ]是指从1节点指向2节点的距离,也可以表示不存在
int dist[N];//distance(距离)的缩写,代表每一个点到源点的距离
bool st[N];//state(状态)的缩写,当st[n]为true时说明这个点到源点的距离最小值就已经确定了
int dijkstra(){
memset(dist,0x3f,sizeof(dist));//存储每一个点到源点的距离
dist[1]=0;//源点到自己的距离为0
for(int i=0;i<n-1;i++){
int t=-1;
for(int j=1;j<=n;j++){
if(!st[j] and (t==-1 or dist[t]>dist[j])){
t=j;//!st[j]指的是最近距离还没有确定的点,and后面就是找符合!st[j]条件的距离最小的点
//这一个操作就是找到未确定最小值的 `点集`中的最小点,t==-1是当第一次遇到未确定~的点时能够被初始化
}
}
//(1)
for(int j=1;j<=n;j++){
dist[j]=min(dist[j],dist[t]+g[t][j]);
}
st[t]=true;//当前t点已经把其余点全部遍历了一遍,此点变成确定距离为最小的点了,这条语句放在(1)处也能AC
}
if(dist[n]==0x3f3f3f3f){//当前点n没被修改,说明到不了点n,输出-1
return -1;
}else{
return dist[n];//易证
}
}
int n, m, s; // 点的数量
vector<PII> g[N]; // 邻接表存储所有边
int dist[N]; // 存储所有点到1号点的距离
bool st[N]; // 存储每个点的最短距离是否已确定
// 求1号点到n号点的最短距离,如果不存在,则返回-1
void dijkstra(){
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({0, 1}); // first存储距离,second存储节点编号
while (heap.size()){
auto t = heap.top();
heap.pop();
int ver = t.second, distance = t.first;
if (st[ver]) continue;
st[ver] = true;
for (auto [v, w]:g[ver]){
if (dist[v] > distance + w){
dist[v] = distance + w;
heap.push({dist[v], v});
}
}
}
}
最小生成树
prim
/*
S:当前已经在联通块中的所有点的集合
1. dist[i] = inf
2. for n 次
t<-S外离S最近的点
利用t更新S外点到S的距离
st[t] = true
n次迭代之后所有点都已加入到S中
联系:Dijkstra算法是更新到起始点的距离,Prim是更新到集合S的距离
*/
int g[N][N], dist[N];
//邻接矩阵存储所有边
//dist存储其他点到 集合S 的距离
bool st[N];
int prim() //如果图不连通返回INF, 否则返回res
{
memset(dist, INF, sizeof dist);
int res = 0;
for(int i = 0; i < n; i++) {
int t = -1;
for(int j = 1; j <= n; j++) //寻找离集合S最近的点
if(!st[j] && (t == -1 || dist[t] > dist[j]))
t = j;
if(i && dist[t] == INF) return INF; //判断是否连通,有无最小生成树
if(i) res += dist[t]; //更新最新S的权值和
//cout << i << ' ' << res << endl;
st[t] = true;
for(int j = 1; j <= n; j++) dist[j] = min(dist[j], g[t][j]);
}
return res;
}
---------------------------------------------------------------
cin >> n >> m;
int u, v, w;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
if(i ==j) g[i][j] = 0;
else g[i][j] = INF;
while(m--) {
cin >> u >> v >> w;
g[u][v] = g[v][u] = min(g[u][v], w);
}
int t = prim();
//临时存储防止执行两次函数导致最后仅返回0
if(t == INF) puts("impossible");
else cout << t << endl;
Kruskal
void kruskal()
{
int res = 0, cnt = 0;
for (int i = 1; i <= m; i++)//依次尝试加入每条边
{
int a = find(g[i].a), b = find(g[i].b);// a,b 点所在的集合
if (a != b)//如果 a b 不在一个集合中
{
res += g[i].c;//a b 之间这条边要
cnt++;// 保留的边数量+1
p[a] = b;// 合并a b
}
}
}
---------------------------------------------------------------
struct node {
int a, b, c;
}g[N];
bool cmp(node a, node b)
{
return a.c < b.c;
}
---------------------------------------------------------------
int find(int x)//并查集找祖宗
{
if (p[x] == x) return p[x];
return p[x]=find(p[x]);
}
---------------------------------------------------------------
for(int i = 1;i <= m;i ++)
{
int u, v, w;
cin >> u >> v >> w;
g[i] = { u, v, w };
}
---------------------------------------------------------------
if (cnt == n - 1) cout << res << endl;//只有加入集合的边数为n-1才有解
else puts("orz");
Floyd
void floyd()
{
for (int k = 1; k <= n; k ++ )
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= n; j ++ )
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
--------------------------------------------------------------
while (m -- )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
d[a][b] = min(d[a][b], c);
}
floyd();
第四章、数学知识
质数(重点掌握)
线性筛
const int N=10000010;
int primes[N],cnt;
bool st[N];
//线性筛 筛选1-n里面的质数
void get_primes(int n){
for(int i=2;i<=n;i++)
{
if(!st[i]) primes[cnt++]=i;
for(int j=0;primes[j]<=n/i;j++)
{
st[primes[j]*i]=1;
if(i%primes[j]==0) break;
}
}
}
---------------------------------------------------------------
int n;
cin>>n;
get_primes(n);
cout<<cnt<<endl;
约数(重点掌握模板就行)
//求约数(要理解)
void get_y(int n){
for(int i=1;i<=n/i;i++)
{
if(n%i==0)
{
y[cnt++]=i;
if(n/i!=i) y[cnt++]=n/i;
}
}
}
---------------------------------------------------------------
cin>>n;
get_y(n);
for(int i=0;i<cnt;i++) cout<<y[i]<<" ";
cout<<endl;
快速幂(会用模板就行)
typedef long long ll;
// 快速幂,o(K) 快速求出 a^k %mod
int qkpow(int a,int k){
int res = 1;
while(k){
if(k&1)res = (ll)res*a%mod;
k>>=1;
a = (ll)a*a%mod;
}
return res;
}
---------------------------------------------------------------
int a,k;
cin>>a>>k;
cout<<qkpow(a,k)<<endl
第五章、动态规划
背包问题
记忆化搜索
第六章、贪心(学会经典案例)
区间选点
给定 N 个闭区间 [ai,bi],请你在数轴上选择尽量少的点,使得每个区间内至少包含一个选出的点。
输出选择的点的最小数量。
//1将每个区间按照右端点从小到大进行排序
//2从前往后枚举区间,end值初始化为无穷小
struct Range
{
int l, r;
}range[N];
---------------------------------------------------------------
bool cmp(Range a,Range b)
{
return a<b;
}
---------------------------------------------------------------
for (int i = 0; i < n; i ++ )
cin>>range[i].l>>range[i].r;
sort(range, range + n,cmp);
---------------------------------------------------------------
for (int i = 0; i < n; i ++ )
if (ed < range[i].l)// 如果本次区间不能覆盖上次区间的右端点
{
res ++ ;//则需要选择新的点
ed = range[i].r;
}
cout<<res<<endl;
最大不相交区间数量
给定 N个闭区间 [ai,bi],请你在数轴上选择若干区间,使得选中的区间之间互不相交(包括端点)。
输出可选取区间的最大数量。
struct Range
{
int l, r;
}range[N];
---------------------------------------------------------------
bool cmp(Range a,Range b)
{
return a<b;
}
---------------------------------------------------------------
for (int i = 0; i < n; i ++ )
cin>>range[i].l>>range[i].r;
sort(range, range + n,cmp);
---------------------------------------------------------------
for (int i = 0; i < n; i ++ )
if (ed < range[i].l)
{
res ++ ;
ed = range[i].r;
}
cout<<res<<endl;
区间分组
给定 N 个闭区间[ai,bi]],请你将这些区间分成若干组,使得每组内部的区间两两之间(包括端点)没有交集,并使得组数尽可能小。
输出最小组数。
struct Range
{
int l, r;
}range[N];
---------------------------------------------------------------
bool cmp(Range a,Range b)
{
return a<b;
}
---------------------------------------------------------------
cin>>n;
for (int i = 0; i < n; i ++ )
{
int l, r;
cin>>l>>r;
range[i] = {l, r};
}
sort(range, range + n,cmp);
priority_queue<int, vector<int>, greater<int>> heap;
--------------------------------------------------------------
for (int i = 0; i < n; i ++ )
{
auto r = range[i];
if (heap.empty() || heap.top() >= r.l) heap.push(r.r);
//如果一个区间的左端点比最小组的右端点要小,就开一个新组
else
{
heap.pop();
heap.push(r.r);
// 如果一个区间的左端点比最小组的右端点要大,则放在该组
}
}
cout<<heap.size()<<endl;
区间覆盖
给定 N个闭区间 [ai,bi] 以及一个线段区间 [s,t][s,t],请你选择尽量少的区间,将指定线段区间完全覆盖。
输出最少区间数,如果无法完全覆盖则输出 −1
//1将所有区间按照左端点从小到大进行排序
//2从前往后枚举每个区间,在所有能覆盖start的区间中,选择右端点的最大区间,然后将start更新成右端点的最大值
struct Range
{
int l, r;
}range[N];
---------------------------------------------------------------
bool cmp(Range a,Range b)
{
return a<b;
}
---------------------------------------------------------------
int st, ed;
cin>>st>>ed;
cin>>n;
for (int i = 0; i < n; i ++ )
{
int l, r;
cin>>l>>r;
range[i] = {l, r};
}
sort(range, range + n,cmp);
---------------------------------------------------------------
int res = 0;
bool success = 0;
for (int i = 0; i < n; i ++ )
{
int j = i, r = -2e9;
//判断左端点在st之前的区间,循环找到最大右端点,如果右端点也在st之前,说明无法覆盖
while (j < n && range[j].l <= st)
{
r = max(r, range[j].r);
j ++ ;
}
if (r < st)//如果右端点也在st之前,说明无法覆盖
{
res = -1;
break;
}
res ++ ;
//每循环一次,没有在前面跳出的话,说明找到了一个区间,res++
if (r >= ed)
{
success = 1;
break;
}
st = r;
i = j - 1;
//把st更新成r,保证后面的区间适合之前的区间有交集,从而形成对整个序列的覆盖
}
if (!success) res = -1;
cout<<res<<endl;
//如果遍历了所有的数组,还是没有覆盖最后的end,说明不能成功
}
合并果子
例如有 3 种果子,数目依次为 1,2,9。可以先将 1、2 堆合并,新堆数目为 3,耗费体力为 3。接着,将新堆与原先的第三堆合并,又得到新的堆,数目为 12,耗费体力为 12。所以达达总共耗费体力=3+12=15。可以证明 15 为最小的体力耗费值。
cin>>n;
priority_queue<int, vector<int>, greater<int>> heap;
while (n -- )
{
int x;
scanf("%d", &x);
heap.push(x);
}
---------------------------------------------------------------
int res = 0;
while (heap.size() > 1)
{
int a = heap.top(); heap.pop();
int b = heap.top(); heap.pop();
res += a + b;
heap.push(a + b);
}
cout<<res;
排队打水
有 nn 个人排队到 11 个水龙头处打水,第 ii 个人装满水桶所需的时间是 titi,请问如何安排他们的打水顺序才能使所有人的等待时间之和最小?
cin >> n;
for(int i = 0; i < n; i ++) cin >> a[i];
sort(a, a + n);
// int res = 0, t = 0;
LL res = 0, t = 0;
for(int i = 0; i < n; i ++)
{
res += t;
t += a[i];
}
cout << res;
货仓选址
在一条数轴上有 N 家商店,它们的坐标分别为 A1∼AN。现在需要在数轴上建立一家货仓,每天清晨,从货仓到每家商店都要运送一车商品。为了提高效率,求把货仓建在何处,可以使得货仓到每家商店的距离之和最小。
cin>>n;
for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);
sort(q, q + n);
int res = 0;
for (int i = 0; i < n; i ++ ) res += abs(q[i] - q[n / 2]);
cout<<res;
耍杂技的牛
这 N 头奶牛中的每一头都有着自己的重量 Wi以及自己的强壮程度 Si。一头牛支撑不住的可能性取决于它头上所有牛的总重量(不包括它自己)减去它的身体强壮程度的值,现在称该数值为风险值,风险值越大,这只牛撑不住的可能性越高。您的任务是确定奶牛的排序,使得所有奶牛的风险值中的最大值尽可能的小。
typedef long long ll;
typedef pair<int, int> PII;
const int N = 5e4 + 5;
PII a[N];
int n;
cin >> n;
for(int i = 0; i < n; i ++ )
{
int x, y;
cin>>x>>y;
a[i].first = x + y;
a[i].second = y;
}
sort(a, a + n);
ll res = -1e18, sum = 0;
for(int i = 0; i < n; i ++ )
{
sum -= a[i].second;
res = max(res, sum);
sum += a[i].first;
}
cout << res << endl;




















 1857
1857

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








