本文探讨了原子弹爆炸能量的估算方法，通过量纲分析法建立了数学模型，考虑了时间、能量、空气密度和大气压强等因素。采用泰勒的计算方法和最小二乘法拟合，对爆炸能量进行了精确估算。
原子弹爆炸的能量估计
基本想法
冲击波的爆炸由“蘑菇云”反映出来，“蘑菇云”越大，扩散速度越快，能量越大。
假设：爆炸产生的冲击波以爆炸点为中心呈球面向四周传播，爆炸的能量越大，在一定时刻冲击波传播的越远。
泰勒测量：时刻t所对应的“蘑菇云” 的半径r
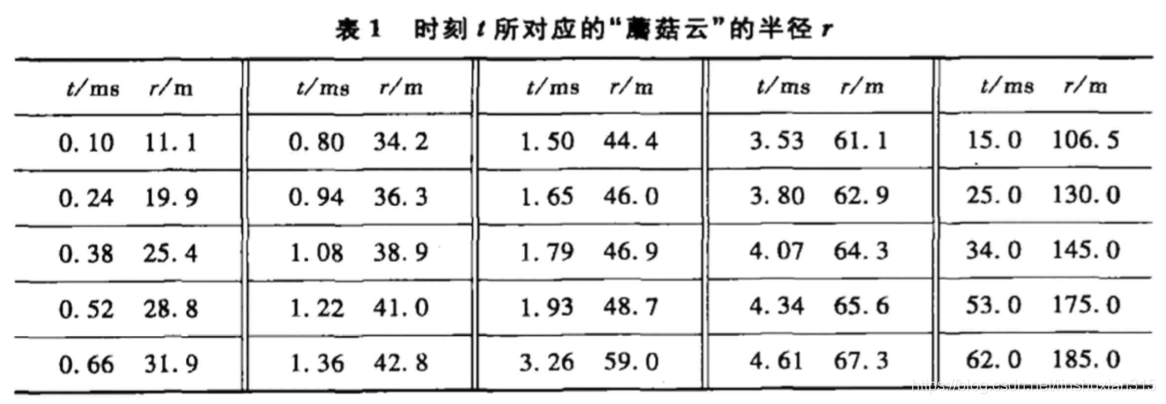泰勒用量纲分析法建立数学模型，辅以小型试验，又利用测量数据对爆炸的能量进行估计。
量纲分析法
量纲齐次原则
| 动力学中基本量纲 | 导出量纲 |
|---|---|
| 长度l的量纲L[l] | 速度v的量纲[v]=LT-1 |
| 质量m的量纲M[m] | 加速度a的量纲[a]=LT-2 |
| 时间t的量纲T[t] | 力f的量纲[f]=LMT-2 |
引力常数k的量纲[k] ( f = k m 1 m 2 r 2 f=k\frac{m_1m_2}{r^2} f=kr2m1m2)
[ k ] = [ f ] [ l ] 2 [ m ] − 2 = L 3 M − 1 T − 2 [k]=[f][l]^2[m]^{-2}=L^3M^{-1}T^{-2} [k]=[f][l]2[m]−2=L3M−1T−2
对无量纲量 α，α=1(=L0M0T0)
eg.单摆运动
求摆动周期的表达式
设物理量t，m，l，g之间有关系式， t = λ m α 1 l α 2 g a 3 ( 1 ) t=λm^{α_1}l^{α_2}g^{a_3}\quad(1) t=λmα1lα2ga3(1)
α 1 , α 2 , α 3 为 待 定 系 数 ， λ 为 无 量 纲 量 α_1,α_2,α_3为待定系数，λ为无量纲量 α1,α2,α3为待定系数，λ为无量纲量
( 1 ) 的 量 纲 表 达 式 [ t ] = [ m ] α 1 [ l ] α 2 [ g ] α 3 (1)的量纲表达式[t]=[m]^{α_1}[l]^{α_2}[g]^{α_3} (1)的量纲表达式[t]=[m]α1[l]α2[g]
最低0.47元/天 解锁文章
扫一扫
到【灌水乐园】发言
