【11.7】数学思维-解最小好进制

一、题目

        以字符串的形式给出 n , 以字符串的形式返回 n 的最小 好进制  。

        如果 n 的  k(k>=2) 进制数的所有数位全为1，则称 k(k>=2) 是 n 的一个 好进制 。

示例 1：

输入：n = "13"
输出："3"
解释：13 的 3 进制是 111。

示例 2：

输入：n = "4681"
输出："8"
解释：4681 的 8 进制是 11111。

示例 3：

输入：n = "1000000000000000000"
输出："999999999999999999"
解释：1000000000000000000 的 999999999999999999 进制是 11。

提示：

• n 的取值范围是 [3, 10^18]
• n 没有前导 0

二、解题思路

        题目要求找到最小的好进制 k，使得 n 在 k 进制下的表示全为 1。换句话说，我们需要找到一个 k 和 m，使得：

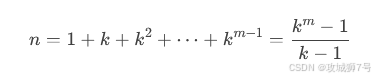
其中，m 是 1 的个数，k 是进制。

范围限制：

        k 的范围是 k≥2。

        m 的范围是 m≥2（因为至少需要两个 1）。

数学推导：

 

优化：

        m的最大值可以通过 log2​(n) 来确定，因为 k≥2 时，m 的最大值是 log2​(n)。

        对于每个 m，我们可以通过二分查找来确定是否存在一个整数 k 满足 n=((k^m) −1)/(k−1)。

三、代码实现

#include <iostream>
#include <string>
#include <cmath>
#include <algorithm>

using namespace std;

// 将字符串转换为长整型
long long stringToLong(const string& s) {
    long long result = 0;
    for (char c : s) {
        result = result * 10 + (c - '0'); // 将字符转换为数字并累加
    }
    return result;
}

// 计算 k^m
long long power(long long k, int m) {
    long long result = 1;
    for (int i = 0; i < m; ++i) {
        result *= k; // 累乘计算 k 的 m 次方
    }
    return result;
}

// 检查是否存在 k 满足 n = (k^m - 1) / (k - 1)
long long findK(long long n, int m) {
    // 二分查找的范围：k 的最小值是 2，最大值是 n^(1/(m-1)) + 1
    long long left = 2, right = pow(n, 1.0 / (m - 1)) + 1;

    while (left <= right) {
        long long mid = (left + right) / 2; // 取中间值
        long long sum = 0; // 用于计算 1 + k + k^2 + ... + k^(m-1)
        long long current = 1; // 当前项的值，初始为 k^0 = 1

        // 计算 1 + k + k^2 + ... + k^(m-1)
        for (int i = 0; i < m; ++i) {
            sum += current; // 累加当前项
            if (sum > n) break; // 如果 sum 已经大于 n，提前退出
            current *= mid; // 计算下一项
        }

        // 判断 sum 是否等于 n
        if (sum == n) {
            return mid; // 找到满足条件的 k
        } else if (sum < n) {
            left = mid + 1; // sum 小于 n，调整左边界
        } else {
            right = mid - 1; // sum 大于 n，调整右边界
        }
    }

    return -1; // 未找到满足条件的 k
}

// 主函数：找到最小的好进制 k
string smallestGoodBase(string n) {
    long long num = stringToLong(n); // 将字符串转换为长整型
    long long result = num - 1; // 默认结果是 n-1（即 k=num-1 时，m=2）

    // 枚举 m 的可能值（m 是 1 的个数）
    for (int m = 2; m <= 60; ++m) {
        long long k = findK(num, m); // 查找是否存在满足条件的 k
        if (k != -1) {
            result = min(result, k); // 更新最小的 k
        }
    }

    return to_string(result); // 返回结果
}

int main() {
    string n;
    cout << "请输入 n: ";
    cin >> n; // 输入 n

    string result = smallestGoodBase(n); // 计算最小好进制
    cout << "最小好进制是: " << result << endl; // 输出结果

    return 0;
}

时间复杂度：

        枚举 m 的复杂度是 O(logn)。

        对于每个 m，二分查找的复杂度是O(logn)。

        总复杂度为 O((logn)^2)。

空间复杂度：

        只使用了常数级别的额外空间，空间复杂度为 O(1)。

        通过数学推导和二分查找，我们可以高效地找到最小的好进制 k