移动均值滤波和线性回归滤波 MATLAB数据处理1

原创已于 2022-12-08 21:14:11 修改 · 4.1k 阅读

46 ·

CC 4.0 BY-SA版权

文章标签：

#均值算法 #线性回归 #matlab

于 2022-12-08 12:24:05 首次发布

数据处理专栏收录该内容

1 篇文章

订阅专栏

本文详细介绍了MATLAB中两种数据平滑方法：移动均值滤波和Savitzky-Golay滤波。移动均值滤波通过计算数据点附近的平均值进行平滑，而Savitzky-Golay滤波利用多项式进行平滑，更好地保留数据特征。此外，文章还提到了局部回归平滑的Lowess和Loess方法，以及中值滤波的应用。

1.移动均值滤波 Moving Average Filtering

移动平均滤波器通过用范围内定义的相邻数据点的平均值替换每个数据点来平滑数据。该过程等效于低通滤波，其平滑响应由差分方程给出

$y_s(i)=\frac{1}{N+1}(y(i+N)+y(i+N-1)+...+y(i-N))$

其中 $y_s(i)$ 是第i个数据点的平滑值，N是 $y_s(i)$ 两侧相邻的点的数量，2N+1是跨度

如果默认5阶，就相当于自己加上自己的前两个和后两个，然后除以5

如果使用Curve Fitting Toolbox（MATLAB指令：cftool）工具必须满足：

跨度必须是奇数（其实偶数也没问题，只要不是0,2，MATLAB会自动把偶数减一处理）
要平滑的数据点必须位于跨度的中心。
对于不能容纳任意一侧指定数量邻居的数据点，调整跨度。
端点不会平滑，因为无法定义跨度。

smooth函数，默认的跨度是5,可以用公式表示：

ys(1) = y(1)
ys(2) = (y(1)+y(2)+y(3))/3
ys(3) = (y(1)+y(2)+y(3)+y(4)+y(5))/5
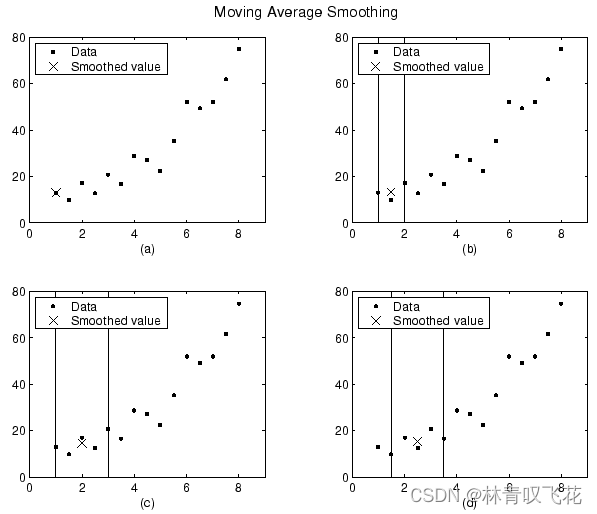
ys(4) = (y(2)+y(3)+y(4)+y(5)+y(6))/5

生成的数据集的前四个数据点的平滑值和跨度如下所示，形象表示平移的原理

第一个点就等于第一个点，第二个值为前三个的均值，第三个值为前五个均值，第四个值为2到6的均值，以此类推，倒数第一和倒数第二与前两个同理。

2.Savitzky-Golay 滤波 Savitzky-Golay Filtering

Savitzky-Golay（萨维茨基·戈莱）滤波可以被认为是一种广义的移动平均。通过使用给定次数的多项式执行未加权线性最小二乘拟合，可以导出滤波器系数。因此，Savitzky-Golay滤波器也称为数字平滑多项式滤波器或最小二乘平滑滤波器。

注意，更高阶的多项式可以实现高水平的平滑而不衰减数据特征。

Savitzky-Golay滤波方法通常用于频率数据或光谱（峰值）数据。对于频率数据，该方法在保留信号的高频分量方面是有效的。对于光谱数据，该方法在保留峰值的较高矩（如线宽）方面是有效的。相比之下，移动平均滤波器倾向于滤除信号的高频成分的很大一部分，并且它只能保留峰值的低阶矩，例如质心（还是形心）。然而，Savitzky-Golay滤波在抑制噪声方面不如移动平均滤波器成功。

曲线拟合工具箱软件使用的Savitzky Golay平滑方法遵循以下规则：

跨度必须是奇数
多项式次数必须小于跨度。
数据点不需要具有均匀的间距。

通常，Savitzky-Golay滤波需要预测数据的均匀间隔。但是，曲线拟合工具箱算法支持非均匀间距。因此，不需要执行额外的过滤步骤来创建具有均匀间距的数据。

下图显示了生成的高斯数据和使用Savitzky-Golay方法进行平滑的多次尝试。数据非常嘈杂，峰值宽度从宽到窄不等。跨度等于数据点数量的5%。

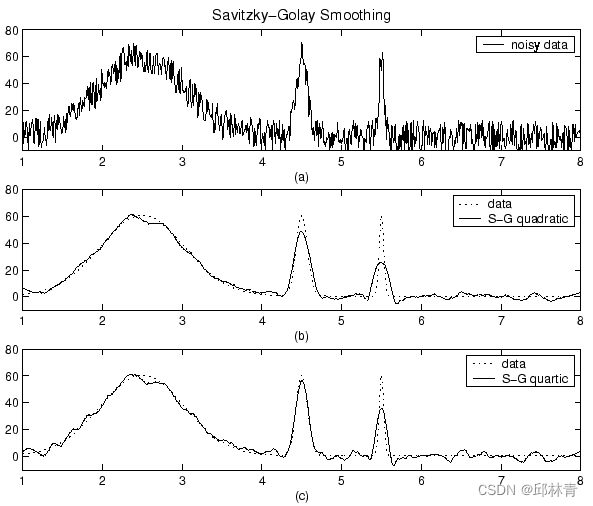
图（b）显示了用二次多项式进行平滑的结果。请注意，该方法对于窄峰表现不佳。图（c）显示了用四次多项式进行平滑的结果。通常，高次多项式可以更准确地捕捉窄峰的高度和宽度，但在平滑较宽峰时效果不佳。

3.局部回归平滑

3.1 Lowess and Loess

“lowess”和“loess”的名称源自术语“局部加权散点图平滑locally weighted scatter plot smooth”，因为这两种方法都使用局部加权线性回归来平滑数据。

平滑过程被认为是局部的，因为与移动平均法一样，每个平滑值都由范围内定义的相邻数据点确定。该过程是加权的，因为为范围内包含的数据点定义了回归权重函数。除了回归权重函数之外，您还可以使用一个鲁棒的权重函数，它可以使过程抵抗异常值。

最后，通过回归中使用的模型来区分这些方法：lowess使用一次多项式（对应MATLAB工具箱中的linear polynomial），而loess使用二次多项式（对应MATLAB工具箱中的quadratic polynomial）。

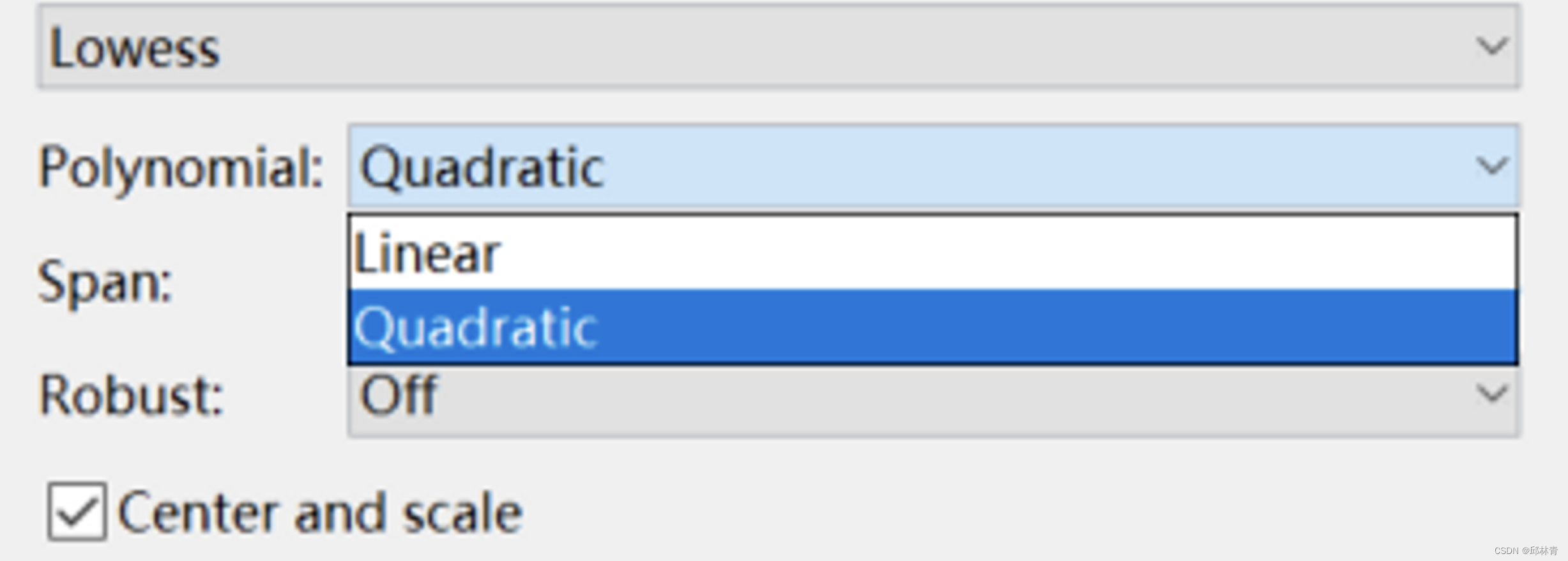
曲线拟合工具箱软件使用的局部回归方法遵循以下规则：

跨度奇偶都行
可以将跨度指定为数据集中数据点总数的百分比。例如，0.1的跨度使用10%的数据点。

3.2 The Local Regression Method

对于每个数据点，局部回归平滑过程遵循以下步骤：

计算跨度中每个数据点的回归权重。权重由如下所示的三次方函数给出。
$w_i=(1-|\frac{x-x_i}{d(x)}|)^3$

x是与要平滑的响应值相关联的预测值，xi是由跨度定义的x的最近邻，d（x）是x到跨度内最远预测值的横坐标距离。权重具有以下特征：
1）要平滑的数据点权重最大，对拟合的影响最大
2）跨度外的数据点没有权重，对拟合没有影响。
进行加权线性最小二乘回归。对于lowess，回归使用一次多项式。对于loess，回归使用二次多项式。
平滑值由感兴趣的预测值处的加权回归给出。

如果平滑计算涉及平滑数据点两侧相同数量的相邻数据点，则权重函数是对称的。然而，如果相邻点的数量关于平滑数据点不是对称的，则权重函数不是对称的。注意，与移动平均平滑过程不同，跨度从不改变。例如，当使用最小预测值平滑数据点时，权重函数的形状将被截断一半，跨度中最左侧的数据点具有最大权重，所有相邻点都位于平滑值的右侧。

对于31个数据点的跨度，端点和内部点的权重函数如下所示。

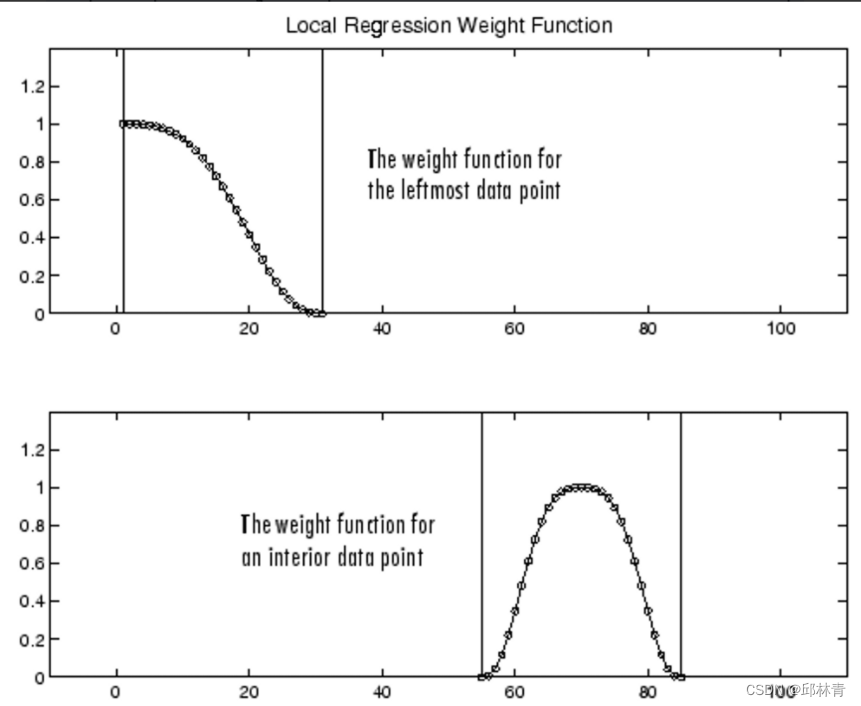
使用跨度为5的lowess方法，生成数据集前四个数据点的平滑值和相关回归如下所示。

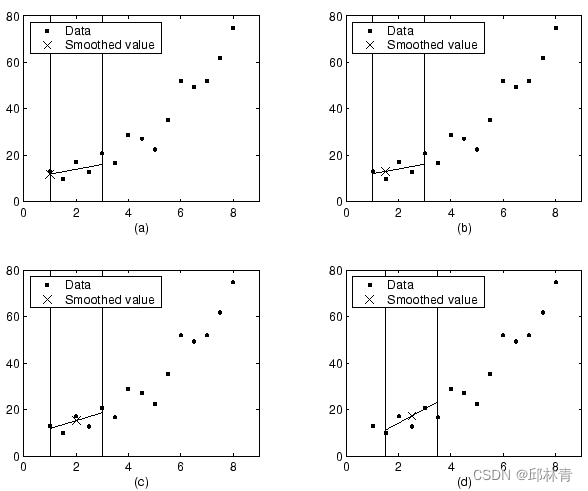
随着平滑过程从数据点到数据点的进行，跨度不会改变。然而，根据最近邻居的数量，回归权重函数可能对要平滑的数据点不是对称的。特别地，曲线（a）和（b）使用不对称权重函数，而曲线（c）和（d）使用对称权重函数。

对于loess法，除了平滑值将由二次多项式生成外，图形看起来相同。

3.3 Robust Local Regression

如果数据包含异常值，则平滑值可能会失真，并且不会反映大量相邻数据点的行为。为了克服这个问题，可以使用不受小部分异常值影响的稳健过程来平滑数据。

有关异常值的描述，请参阅残差分析。

曲线拟合工具箱软件为lowess和loess平滑方法提供了一个强大的版本。这些稳健方法包括对稳健权重的额外计算，该权重能够抵抗异常值。稳健平滑程序遵循以下步骤：

根据上一节所述的平滑程序计算残差。
计算跨度中每个数据点的鲁棒权重。权重由双平方函数给出，

$w_i=\begin{cases}(1-(r_i/6MAD)^2)^2,&\text{if } |r_i|<6MAD, \\0, &\text{if } |r_i|\geq6MAD, \end{cases}$
这里对应MATLAB工具箱中下图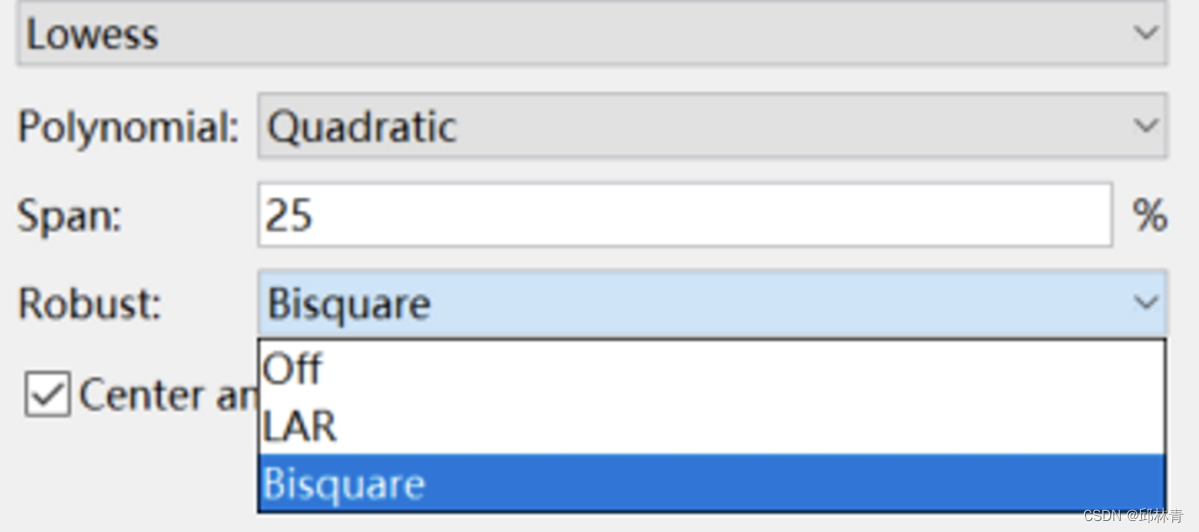

其中ri是通过回归平滑过程产生的第i个数据点的残差，MAD是残差的中值绝对偏差
$MAD=median(|r|)$
中值绝对偏差是残差分布程度的量度。如果ri小于6MAD，则稳健权重接近1。如果ri大于6MAD，稳健权重为0，相关数据点被排除在平滑计算之外。
使用稳健权重再次平滑数据。使用局部回归权重和鲁棒权重计算最终平滑值。
重复前面的两个步骤，总共五次迭代。

下面将lowess过程的平滑结果与包含单个异常值的生成数据集的鲁棒lowess过程结果进行比较。两个程序的跨度为11个数据点。

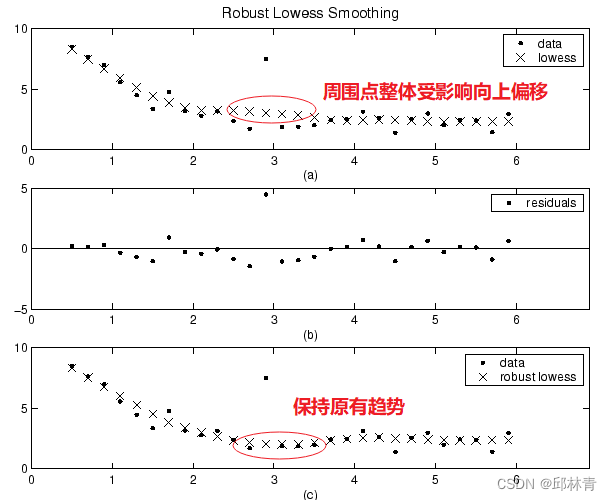
曲线图（a）显示，异常值影响几个相邻数据的平滑值。图（b）表明，异常值的残差大于六个中值绝对偏差。因此，该数据点的鲁棒权重为零。曲线图（c）显示了与异常值相邻的平滑值反映了数据正常的趋势。

4.MATLAB实例与代码

在MATLAB中试验各种滤波效果

clc;
clear;
aa = sin(0:pi/100:pi);       %sin0到π，分为100份，一共101个数
bb = randn(101,1);           %随机生成101行1列的服从标准正态分布的数
aa = aa';                    %转置
cc = aa+bb/10;               %加上噪声
plot((0:pi/100:pi),aa,'-k','LineWidth',1); %(0:pi/100:pi),
hold on;                     %保持原图
plot((0:pi/100:pi),cc,'-r'); %在pi内画出cc
dd = smooth(cc,5);           %均值滤波   默认是周围5个数据进行移动平均 21代表周围20个数中间的数
ff = smooth(cc,21,'lowess'); %线性最小二乘滤波lowess，加权的线性最小二乘滤波loess，
                             %Savitzky-Golay 滤波（'sgolay'），'rlowess'，'rloess'等方法
gg = smooth(cc,21,'loess');
kk = smooth(cc,21,'rlowess');
rr = smooth(cc,21,'rloess');
hold on;                                     %保持原图
plot((0:pi/100:pi),dd,'-y','LineWidth',2);   %画出滤波后的dd  移动均值滤波 黄色
hold on;
plot((0:pi/100:pi),ff,'-g','LineWidth',2);   %lowess 绿色
hold on;
plot((0:pi/100:pi),gg,'-b','LineWidth',2);   %loess 蓝色
hold on;
plot((0:pi/100:pi),kk,'-c','LineWidth',2);   %rlowess 青色
hold on;
plot((0:pi/100:pi),rr,'-m','LineWidth',2);   %rloess 洋红色


%对于这个噪声，加不加r鲁棒，区别不大，奇异值不算严重   
%r之后确实更平滑，所以就看波动到底是不是你想要的，需要波动就不加r，不想要波动就用r
%看出，ff:rlowess更平滑，gg:rloess因为是二次多项式，阶数更高，所以更贴合高点
%w更平滑，如果需要波动就不要w，如果不想要波动就w