概率统计，生日问题，遍历所有可能求解，穷举法

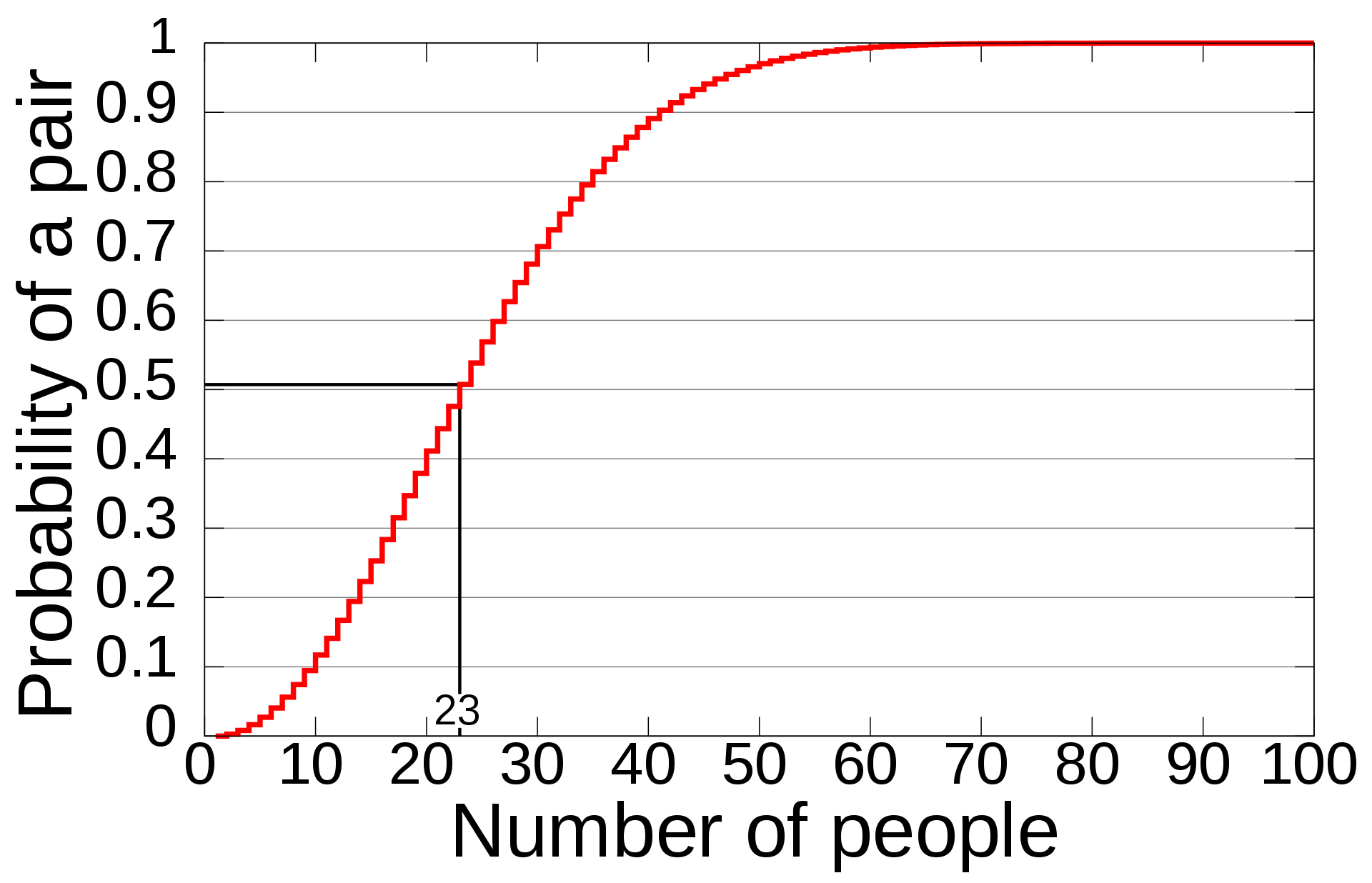
该图片显示特定人数对应的2个人生日一样的概率

如果你手里只有一把锤子，那么你可能会不自觉地把所有东西都当作钉子来看待。——亚伯拉罕·马斯洛，《科学心理学》(1966)

概率论

概率论是一门涉及面非常广的学科。它的应用相当广泛，既可以应用于纯数学领域，有时也会被一些职业赌徒利用。

我们会频繁讨论如何编写和执行代码来检验我们的计算结果是否正确，或者让我们对答案有一定的认识。如果想在 21世纪的劳动大军中获得竞争优势，那么你必须具备编程和模拟的能力。能够写出一个简单的程序来模拟某个问题的100万种可能情况对我们来说是非常有用的，这些结果通常会提醒你留意那些被遗漏的因素或其他错误。

日常的生活体验已经为你提供了足够的背景知识。我只希望能让你对这门课程有个大体的认识，可以把美妙的数学展现在你眼前，并激励你在接下来的几个月里专注地学好这门课并用好本书。

生日问题(表述3)：假设客人的出生日期都是相互独立的，并且每个人都等可能地出生在一年中的任何一天(2月29日除外)，那么房间里有多少人才能保证其中至少两个人的生日在同一天的概率不小于50%？

那么该如何着手研究它呢？ 最常用的方法是考察一些极端情况，并试着从中找出与答案有关的信息。对我们来说，最坏的情形是所有人的生日都不相同。由于我们假设一年只有365天，因此当有366个人出席聚会时就一定会出现“至少两个人的生日在同一天”的情况 (记住，我们假设没有人出生在2月29日)。

另一种极端情况是，如果只有一个人出席聚会，那么显然不可能有两个人的生日在同一天。因此，答案是在2和365之间的某个数。但到底是