证明相对熵的非负性(P22314062汤逸飞，P22314050吴涵，P22314053蒋文海)

最新推荐文章于 2025-12-06 09:40:57 发布

原创最新推荐文章于 2025-12-06 09:40:57 发布 · 632 阅读

16 ·

CC 4.0 BY-SA版权

文章标签：

#信息论 #信息与通信

一、问题引入:

在信息论中，相对熵（Relative Entropy），也称为Kullback-Leibler散度（Kullback-Leibler Divergence，简称KL散度），是两个概率分布之间差异的一种度量。理解相对熵的非负性对于掌握信息论的基本概念至关重要。

二、问题简述：

若 $p_{i}$ 和 $q_{i}$ 是相对于同一信源的两个概念测度，人们通常希望度量概率分布 $p_{i}$ 和 $q_{i}$ 之间的差异，这时需要定义一个量，称为相对熵(relative entropy)。 $p$ 相对于 $q$ 的相对熵定义为：

$D\left (p//q \right )=\sum_{i}^{}p_{i}\log\frac{p_{i}}{q_{i}}$

相对熵具有非负性，下面来证明相对熵的非负性。

三、证明过程：

①当P、Q两信源为离散信源时，此时相对熵的定义为：

$D(P/Q) = \sum_x P(x) \log \frac{P(x)}{Q(x)}, (P(x) \geq 0, Q(x) \geq 0)$

对于任何 $x > 0$ ，有： $\log x \leq x - 1$ ，当且仅当 $x = 1$ 时等号成立。（文末补充证明）

$P(x) = 0$

$P(x) \log \frac{P(x)}{Q(x)} = 0$

∴ $P(x) = 0$ 项不影响结果

∵ $\log \frac{P(x)}{Q(x)} \geq 1 - \frac{Q(x)}{P(x)}, (\log y \geq 1 - \frac{1}{y})$

∴ $P(x) \log \frac{P(x)}{Q(x)} \geq P(x)(1 - \frac{Q(x)}{P(x)}) = P(x) - Q(x)$

∴ $\sum_x P(x) \log \frac{P(x)}{Q(x)} \geq \sum_x P(x) - \sum_x Q(x) = 1 - 1 = 0$

综上可得： $D(P//Q)\geqslant 0$

当且仅当P与Q分布完全一致时，等号成立。

②当P、Q两信源为连续信源时，此时相对熵的定义为：

$D(P \parallel Q) = \int P(x) \log \frac{P(x)}{Q(x)} \, dx$

其中 $P(x)$ 和 $Q(x)$ 是两个概率密度函数，满足 $P(x) \geq 0$ 和 $Q(x) > 0$ ，并且它们的积分都等于1。

对于任何 $x > 0$ ，有： $\log x \geq 1 - \frac{1}{x}$

当且仅当 $x = 1$ 时等号成立。（文末补充证明）

设 $x = \frac{P(x)}{Q(x)}$ ，则： $\log \frac{P(x)}{Q(x)} \geq 1 - \frac{Q(x)}{P(x)}$

将上述不等式代入相对熵的定义中，得到：

$D(P \parallel Q) = \int P(x) \log \frac{P(x)}{Q(x)} \, dx \geq \int P(x) \left( 1 - \frac{Q(x)}{P(x)} \right) \, dx$

简化上述表达式： $D(P \parallel Q) \geq \int P(x) \, dx - \int Q(x) \, dx$

由于 $\int P(x) \, dx = 1$ 和 $\int Q(x) \, dx = 1$ ，上式可改写为： $D(P \parallel Q) \geq 1 - 1 = 0$

综上可得：

$D(P//Q)\geqslant 0$

当且仅当P与Q分布完全一致时，等号成立。

下面来补充证明不等式:

$\ln y\geqslant 1-\frac{1}{y}$

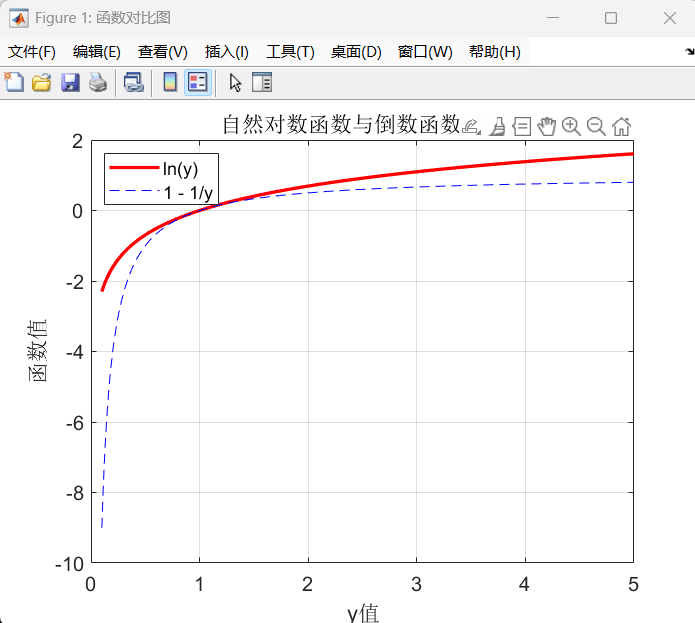
使用MATLEB软件，利用函数图像证明。

代码部分如下：

clear
clc
close all
% 定义y的取值范围（避免y=0时对数无定义的情况）
y_values = linspace(0.1, 5, 491);  % 使用linspace替代冒号运算符
% 使用cellfun计算函数值
funcs = {@(y) log(y), @(y) 1 - 1./y};  % 定义两个匿名函数
f_vals = funcs{1}(y_values);  % 计算第一个函数的值
g_vals = funcs{2}(y_values);  % 计算第二个函数的值
% 创建图形窗口并设置样式
fig = figure('Name', '函数对比图', 'Color', 'white');  % 创建白色背景的图形窗口
ax = axes(fig);  % 创建坐标轴
% 绘制两条函数曲线
plot(ax, y_values, f_vals, 'Color', 'r', 'LineWidth', 2, 'DisplayName', 'ln(y)');
hold on;
plot(ax, y_values, g_vals, 'Color', 'b', 'LineStyle', '--', 'DisplayName', '1 - 1/y');
% 添加坐标轴标签和标题
xlabel('y值');  % x轴标签
ylabel('函数值');  % y轴标签
title('自然对数函数与倒数函数对比');  % 图形标题
% 配置坐标轴和图例样式
grid on;  % 显示网格
set(ax, 'FontSize', 12);  % 设置字体大小
legend('show', 'Location', 'northwest');  % 在左上角显示图例

生成的函数图像如下：