相对熵非负性的证明汪俊磊郎轲刘思雨叶佳佳汪羽辰

Infor_Theory_AHU

于 2024-07-08 20:48:39 发布

阅读量894

点赞数 8

文章标签：信息论

本文链接：https://blog.youkuaiyun.com/lily_ahu/article/details/140277361

版权

相对熵

1.定义

相对熵（也称为KL散度或信息散度）是衡量两个概率分布之间差异的一种方法。若给定两个离散型随机变量的概率分布 $p_{i}$ 和 $q_{i}$ 相对熵被定义为 $p_{i}$ 和 $q_{i}$ 之间的差异：

$D(p \/// q) = \sum_{i} p_i \log \ \frac{p_i}{q_i}$ $(1-1)$

其中 $p_{i}$ 和 $q_{i}$ 分别表示 $P$ 和 $Q$ 分布下随机变量取值为 $i$ 的概率。相对熵的值越大，表示两个分布之间的差异越大。

如果 $P$ 和 $Q$ 是连续型随机变量的概率密度函数，则相对熵的定义为：

$D(p//q)=\int_{-\infty}^{ \infty}p(x)\log\frac{p(x)}{q(x)}dx$ $(1-2)$

其中, $p(x)$ 和 $q(x)$ 分别是 $p$ 和 $q$ 的概率密度函数。

2.性质

（1）非负性

注：当且只有对所有 $i$ , $p_{i},q_{i}$ 时，相对熵为零。

（2）非对称性

相对熵可以看作两个概率测度纸质件的距离，即两个概率测度不同程度的度量，满足以下关系式

$D(p//q) \neq D(q // p)$

相对熵非负性的证明

1.定义法证明

对于概率分布为 $p_{i}$ 的某信源 $x$ ，如果采用编码长度为 $I(p_{i})$ 的方式进行编码，则平均码长为

$H(p) = -\sum_{i} p_i I(p_i) = -\sum_{i} p_i \log p_i$ ,如果采用概率分布为 $q_{i}$ 的码长方式进行编码，每个符

号的编码长度为 $q_{i}$ ，则平均码长为 $-\sum_{i} p_iI(q_{i})=-\sum_{i} p_i \log q_i$ 那么由于两种编码方式的概

率不匹配，使得平均码长增加，增加量即为相对熵：

$-\sum_{i} p_i \log q_i=-[-\sum_{i} p_i \log p_i]=D(p//q)$ ，可知增加量一定是非负的，故得证。

2.利用 Jensen 不等式进行证明

对于凸函数的性质，我们可以写出Jensen不等式如下：

$f(\sum_{i=1}^{n}\lambda _{i}x_{i})\leqslant \sum_{i=1}^{n}\lambda _{i}f(x_{i})$ $(2-1)$

相对熵的数学表达式 $D(p//q)=\sum_{i}^{n}p_{i}log \frac{p_{i}}{q_{i}}$

将 $\frac{p_{i}}{q_{i}}$ 替换成 $x_{i}$ ，原公式转化为：

$D(p//q)=\sum_{i}^{n}q_{i}\cdot x_{i} log x_{i},x\in(0,\infty),q_{i}\in(0,1)$

$(2-2)$

令 $f(x_{i})=x_{i}logx_{i}$ ，上式变为

$D(p//q)=\sum_{i}^{n}q_{i}\cdot f(x_{i}) ,x\in(0,\infty),q_{i}\in(0,1)$

$(2-3)$

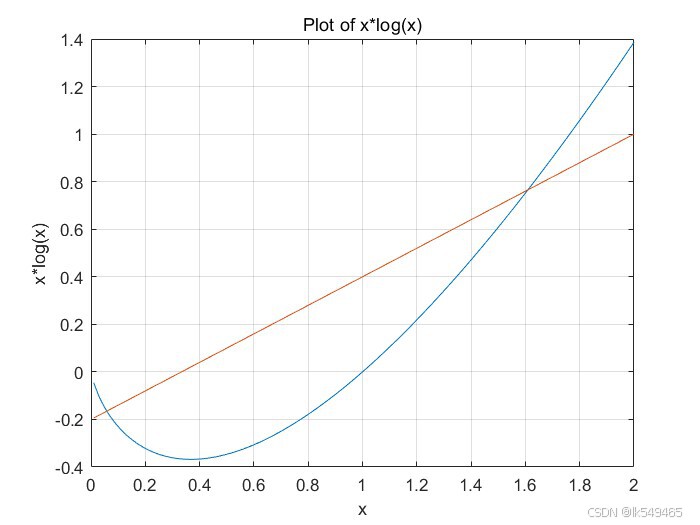
借助MATLAB绘图工具，我们画出了 $f(x_{i})=x_{i}logx_{i}$ 的图像

x = linspace(0.01, 2, 100); 
y1 = x .* log(x);
y2 = 0.6*x - 0.2;
plot(x, y1,x,y2);
xlabel('x');
ylabel('x*log(x)');
title('Plot of x*log(x)');
grid on;

因此我们知道 $f(x_{i})=x_{i}logx_{i}$ 是一个凸函数，满足Jensen不等式。

对上述表达式进行不等式的运算：

$\sum_{i}^{n}q_{i}\cdot f(x_{i})\geqslant f(\sum_{i=1}^{n}q_{i} x_{i})=\sum_{i=1}^{n}q_{i} x_{i}log(\sum_{i=1}^{n}q_{i} x_{i}),x\in(0,\infty),q_{i}\in(0,1)$

$\sum_{i=1}^{n}q_{i} x_{i}log(\sum_{i=1}^{n}q_{i} x_{i})=f(\sum_{i=1}^{n}q_{i} x_{i})=(\sum_{i=1}^{n}q_{i}\cdot \frac{p_{i}}{q_{i}})log(\sum_{i=1}^{n}q_{i}\cdot \frac{p_{i}}{q_{i}})=1\cdot log1=0$