离散无记忆信源的最大熵分布存在性与唯一性证明 （P22314056 胡珂 P22314059 王杨曦）

摘要:

针对离散无记忆信源，本文详细证明当且仅当所有输出符号概率相等时熵达到最大值。通过拉格朗日乘数法和凸性分析两种方法，严格推导出最大熵条件，并结合几何意义和实际应用场景给出信息论解释，同时补充代码验证部分，增强证明的直观性与可信度。

1. 引言 

离散无记忆信源（Discrete Memoryless Source, DMS）是信息论中最基础的信源模型，其核心特点是信源每次输出的符号相互独立，且符号出现的概率不随时间变化。熵作为衡量信源不确定性的关键指标，定义为 :

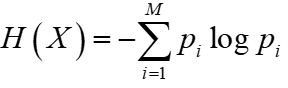
最大熵原理是信息论中的重要准则，它指出：在无额外约束条件下，均匀分布是唯一能使离散无记忆信源熵达到最大值的概率分布。这一原理不仅为信源编码、密码学等领域提供了理论基础，也揭示了 “不确定性最大化” 的内在规律。

下面将通过两种严谨的数学方法证明这一结论，并补充代码验证过程。

2. 问题描述 

设信源输出M个符号

概率分布为

其中，满足：

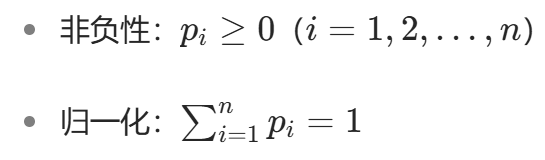
求解：