离散信源最大熵定理的证明 P22214008 孙博航 P22214007 李天天-优快云博客

本文链接：https://blog.youkuaiyun.com/lily_ahu/article/details/140280740

1. 定义和背景介绍

信息熵（Information Entropy）由克劳德·香农（Claude Shannon）在1948年的论文《通信的数学理论》中提出，用来衡量信息的不确定性或信息量。信息熵是信息论的核心概念，对于离散随机变量 ( X ) 及其概率分布 ( P(X) )，其熵定义为：

其中 ( P(x) ) 是随机变量 ( X ) 取值为 ( x ) 的概率，求和是为2对 ( X ) 的所有可能取值进行的。熵的单位取决于对数的底数，常用的单位有比特（底数的对数）和纳特（底数为e的自然对数）。

离散信源（Discrete Source）指的是输出离散符号（或状态）的信息源。信源可以是一个字母表、符号集或者其他离散事件的集合。对于离散信源，可以计算其每个符号输出的概率分布，并据此计算其熵。

2. 最大熵定理的陈述

离散信源最大熵定理（Maximal Entropy Theorem for Discrete Sources）可以表述为：对于给定的离散信源，如果符号集合中的所有符号等概率出现，则该信源的熵最大。形式化地，如果离散信源有 ( n ) 个可能的符号，并且每个符号出现的概率均为 ( \frac{1}{n} )，则该信源的熵为：

这意味着在所有可能的概率分布中，均匀分布使得信息熵最大。这个定理在许多信息处理和通信系统中具有重要意义，因为它提供了最不确定性和最大信息量的基准。

3. 证明步骤

考虑一个离散信源，其可能的符号集合为 ( {x_1, x_2, \ldots, x_n} )，每个符号 ( x_i ) 出现的概率为 ( P(x_i) = p_i )。信源的熵 ( H(X) ) 为：

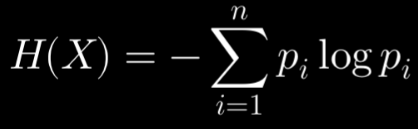
使用拉格朗日乘数法来求最大熵。我们需要最大化熵 ( H(X) )，同时满足概率分布的约束：

构建拉格朗日函数：

对每个 ( p_i ) 和 ( \lambda ) 求偏导数，并令其为零：

从第一个方程中可以解得：

因此，所有的 ( p_i ) 都是相等的，即：

代入到概率约束中验证：

验证成立。因此，当所有符号等概率出现时，熵达到最大值：

4. 应用和意义

离散信源最大熵定理在信息理论中具有重要意义。它表明在给定信源符号个数的情况下，等概率分布的信源具有最大的信息熵，即信息量最大。这意味着在最不确定的情况下，信息量是最大的。

应用示例：

（1)数据压缩：最大熵信源表示数据最难压缩，因为其不确定性最高。所有符号等概率出现时，数据的冗余最少。

（2）密码学：在密码学中，最大熵表示最难预测和破解的密钥分布。因此，理想的密钥应具有最大熵。

（3）通信系统：最大熵信源在通信系统中意味着信道利用效率最高。信源编码和信道编码都基于最大化熵的原则，以提高传输效率和可靠性。

5. 相关文献调研

以下是一些经典和现代的参考文献：

（1）Claude E. Shannon, "A Mathematical Theory of Communication," Bell System Technical Journal, vol. 27, pp. 379-423, 623-656, July, October, 1948：香农的原始论文，是信息论的奠基之作。

（2）Thomas M. Cover and Joy A. Thomas, "Elements of Information Theory," 2nd Edition, Wiley-Interscience, 2006：这本书提供了信息论的详细介绍和许多应用示例。

（3）Robert M. Gray, "Entropy and Information Theory," Springer, 2011：这本书深入探讨了熵和信息论的基本概念及其应用。

（4）David J.C. MacKay, "Information Theory, Inference, and Learning Algorithms," Cambridge University Press, 2003：这本书将信息论与机器学习结合起来，提供了广泛的应用背景。