BSC信道串联后的信道容量
1 信道
1.1 信道基本概念
信道,简言之,就是信息传输的通道,是通信系统的重要组成部分,是传输信息的载体,其主要任务是传输或者存储信息;
信道是信息论的主要研究对象之一,其主要研究内容是在理论上能够传输或者存储的最大信息量,即信道容量。
1.2 信道的分类
根据输入、输出的取值特性:
离散信道:也称为数字信道,该类信道中输入空间、输出空间均为离散事件集合,集合中事件数量是有限的,或者有限可数的,随机变量取值都是离散的;
连续信道:也称为模拟信道,输入空间、输出空间均为连续事件集合,集合中事件的数量是无限的、不可数的;
半离散半连续信道:输入空间、输出空间一个为离散事件集合,而另一个则为连续事件集合,即输入、输出随机变量一个是离散的,另一个是连续的;
波形信道:也称为时间连续信道,信道输入、输出都是时间的函数,而且随机变量的取值都取自连续集合,且在时间(或者空间)上的取值是连续的。
根据噪声的统计特性:
随机差错信道:信道中传输码元所遭受的噪声是随机的、独立的,这种噪声相互之间不关联,码元错误不会成串出现。最具有代表性的是高斯白噪声信道;
突发差错信道:信道中噪声或者干扰对传输码元的影响具有关联性,相互之间不独立,从而使得码元错误往往成串出现。常有的如衰落信道、码间干扰信道。在实际中这种信道经常出现,如移动通信的信道、光盘存储器等。
1.3 二进制对称信道——BSC信道
离散二进制输入,离散二进制输出

它的输入和输出都只有0和1两种符号,并且发送0而接收到1,以及发送1而收到0(即误码)的概率相同,所以称信道是对称的。此时条件差错概率(conditional probability)由p表示。二进制对称信道的转移概率如下图:

2 BSC信道容量计算
2.1 信道容量
信道容量就是指在信道上进行无差错传输所能达到的最大传输速率。对于只有一个信源和一个信宿的单用户信道,它是一个数,单位是比特每秒或比特每符号。它代表每秒或每个信道符号能传送的最大信息量,或者说小于这个数的信息率必能在此信道中无错误地传送。
信道容量是信道的一个参数,它和信源的大小并无必然联系。信道容量有时也表示为单位时间内可传输的二进制位的位数(称信道的数据传输速率,位速率),以位/秒(b/s)形式予以表示,简记为bps。
在数值上信道容量等于找到一种输出符号概率分布使该信道传输的互信息达到最大值。
2.2 单个BSC信道容量
假定BSC的转换概率为P,那么可以将输入和输出写成如下表:
| 0 | 1 | |
| 0 | 1-p | p |
| 1 | p | 1-p |
假定输入为均匀且随机的,也就是取0的概率为1/2,取1的概率也为1/2,根据我们的经验此分布有1比特的熵,来利用香农熵公式简单验证一下:
MATLAB编程验证结果:
信道函数如下:
函数1
function [A] = MYBSC1(I,p)
%MYBSC1 bsc信道函数
% I-输入的二值图像或0,1矩阵;p-BSC信道参数
[m,n]=size(I);
I=reshape(I,m*n,1); %二值矩阵转为列向量
x=rand(m*n,1);
for i=1:m*n
if x(i)<p
x(i)=1;
else
x(i)=0;
end
end
A=xor(I,x);
A=reshape(A,m,n); %列向量转为二值矩阵
end函数2
function [ A ] = MYBSC2(I,p)
%MYBSC2 bsc信道函数
% I-输入的二值图像或0,1矩阵;p-BSC信道参数
[m,n]=size(I);
x=rand(m,n);
for i=1:m
for j=1:n
if x(i,j)<p
x(i,j)=1;
else
x(i,j)=0;
end
end
end
A=xor(I,x);
end通过MATLAB的系统函数与自己编写的函数进行对比验证:
clc
clear all
Pic=imread('star.jpg');
Pi_gray=rgb2gray(Pic); %灰度化
thresh=graythresh(Pi_gray); %灰度阈值
Pi_2=im2bw(Pi_gray,thresh); %二值化
Pi_2=im2double(Pi_2); %将逻辑值转换为双精度
Pi_01=bsc(Pi_2,0.5); %经过bsc信道(系统函数)
MyPi1=MYBSC1(Pi_2,0.5); %自写函数
MyPi2=MYBSC2(Pi_2,0.5);
figure
subplot(2,2,1);imshow(Pic,[]);title('原图');
subplot(2,2,2);imshow(Pi_gray,[]);title('灰度图');
subplot(2,2,3);imshow(Pi_2,[]);title('二值图');
subplot(2,2,4);imshow(Pi_01,[]);title('经过p=0.5bsc信道');
figure
subplot(2,2,1);imshow(Pic,[]);title('原图');
subplot(2,2,2);imshow(Pi_gray,[]);title('灰度图');
subplot(2,2,3);imshow(MyPi1,[]);title('经过信道1,p=0.5');
subplot(2,2,4);imshow(MyPi2,[]);title('经过信道2,p=0.5');

通过经过相同参数的BSC信道后的三幅图片的对比可知,编写的信道函数符合BSC信道。
2.3 马尔可夫链
一句话描述:状态空间中经过从一个状态到另一个状态的转换的随机过程。该过程要求具备无记忆的性质:下一状态的概率分布只能由当前状态决定,在时间序列中它前面的事件均与之无关。
也就是说,马尔可夫链是一个随机系统,它必须满足两个条件:
系统任意时刻可以用有限个可能状态之一来描述;
系统无后效性,即某阶段的状态一旦确定,则此后过程的演变不再受此前各种状态及决策的影响。
在马尔可夫链的每一步,系统根据概率分布,可以从一个状态变到另一个状态,也可以保持当前状态。状态的改变叫做转移,与不同的状态改变相关的概率叫做转移概率。随机漫步就是马尔可夫链的例子。随机漫步中每一步的状态是在图形中的点,每一步可以移动到任何一个相邻的点,在这里移动到每一个点的概率都是相同的(无论之前漫步路径是如何的)。
3 N个相同的BSC信道串联容量
3.1 两个BSC信道串联
首先,从两个信道的串联论述,构建模型框图,如下图所示:

在给定Y之后,Z的取值与X无关,故 。
对于所有的i,j,k,X、Y、Z构成一个马尔科夫链。
故说明这两个信道串联的转移概率为信道1和信道2的转移概率矩阵之积。
3.2 N个BSC信道串联
由此可得推论,N个相同的BSC信道串联,其转移概率矩阵为
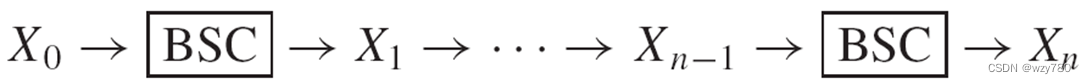
其总体的转移概率矩阵可以计算为:

当𝑛趋于无穷大时,转移概率矩阵的每一项都趋近于0.5。这个串联信道相当于一个𝑓=0.5的BSC信道,而该信道的容量为0 bit,完全不能传递信息。
4 总结
本文主要从模型假设方面对N个BSC信道串联后的信道容量进行了简单的推导证明。
引入了前置知识:信道的概念,单个BSC信道的容量计算,马尔可夫链。
迫于认知不足与知识储备有限,本文只做简单论述,同时借鉴了诸位优快云优秀博主相关方面的优秀科普文章,特别鸣谢:
“小菜菜forever”;“minutiae”;“wmhsjtu”;“X_s_yu彧”;“唠嗑!”;“qq_36488756”
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








