python递归实例：汉诺塔问题

问题实例

注意：一次只能移动一个圆盘，并且小圆盘上不能放大圆盘

以三个圆盘为例的移动过程分析

以三个圆盘为例

第一步

把最上方的小圆盘移动到中间的柱子上

第二步

把绿色圆盘移动到右面的柱子上

第三步

中间的移动到右面

第四步

左面的移动到中间

第五步

右面柱子最上面的圆盘移动到左边柱子

第六步

右面的圆盘移动到中间的柱子

第七步

最左面最小的圆盘移动到中间位置

至此，大功告成！

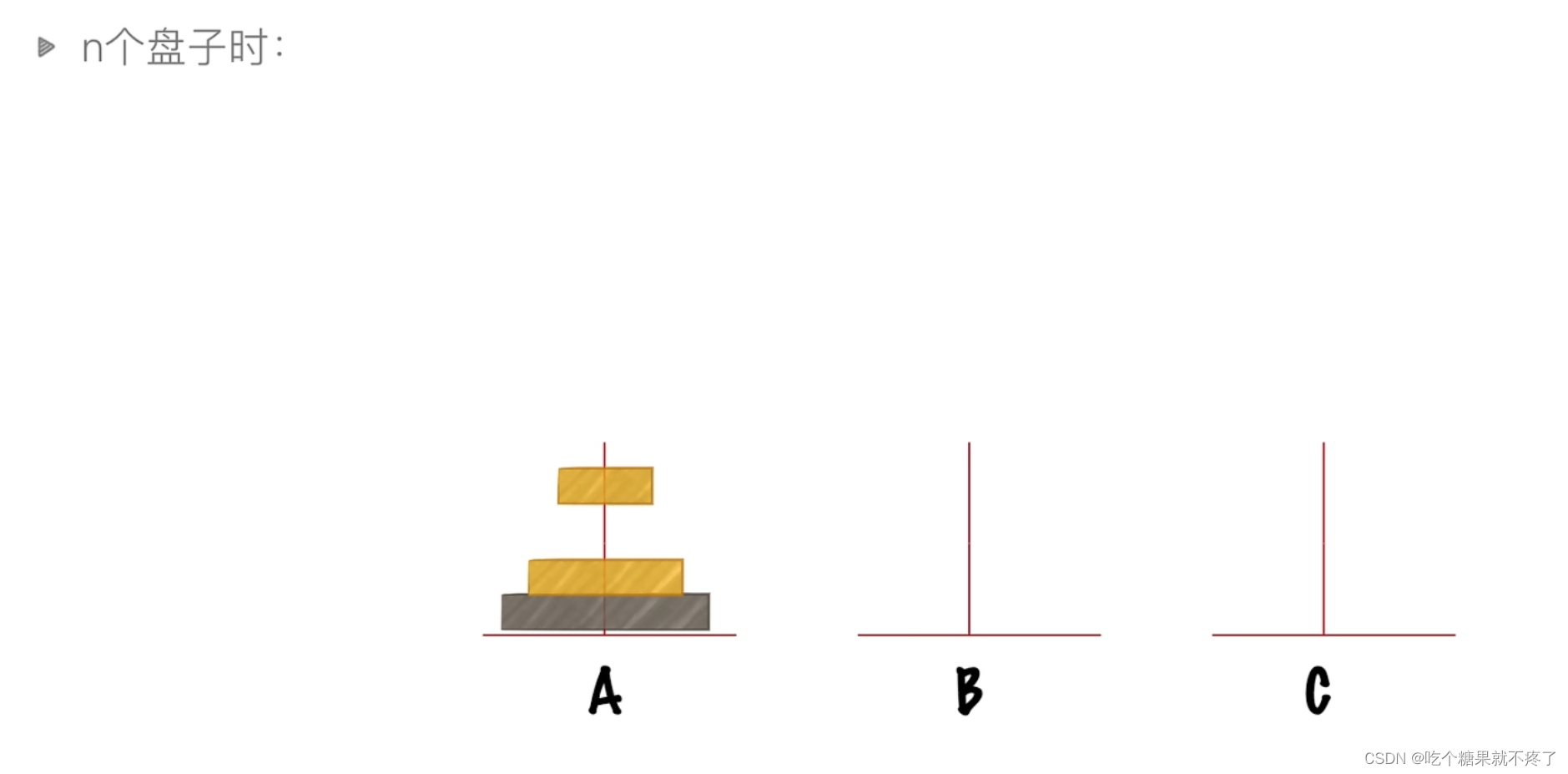
n个盘子分析

n个盘子的初始状态

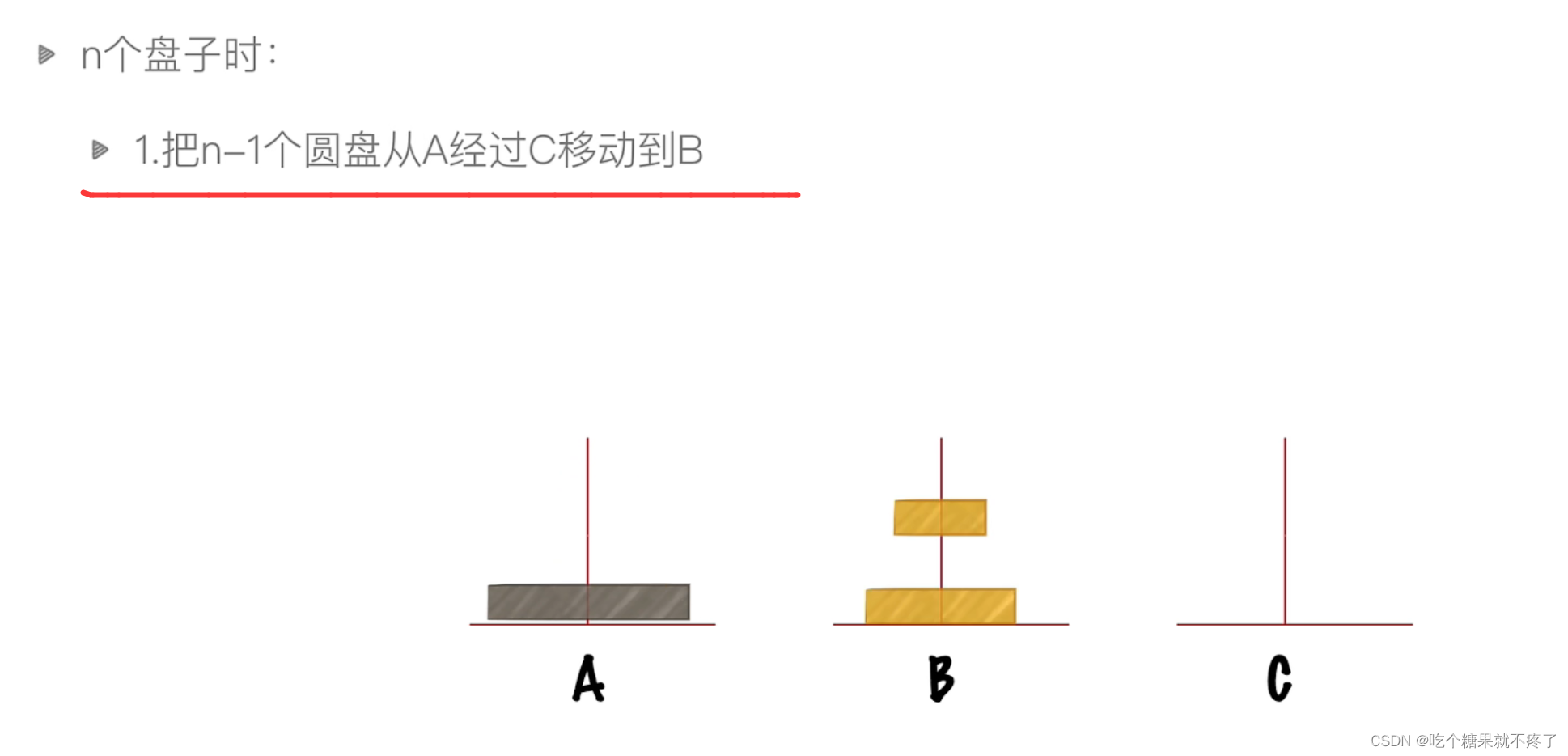
第一步，将上面N-1个盘子看作整体，会经过C，移动到B
这一步不明白的，可以自行模拟4-5个盘子尝试，亲测是可以的

第二、三步

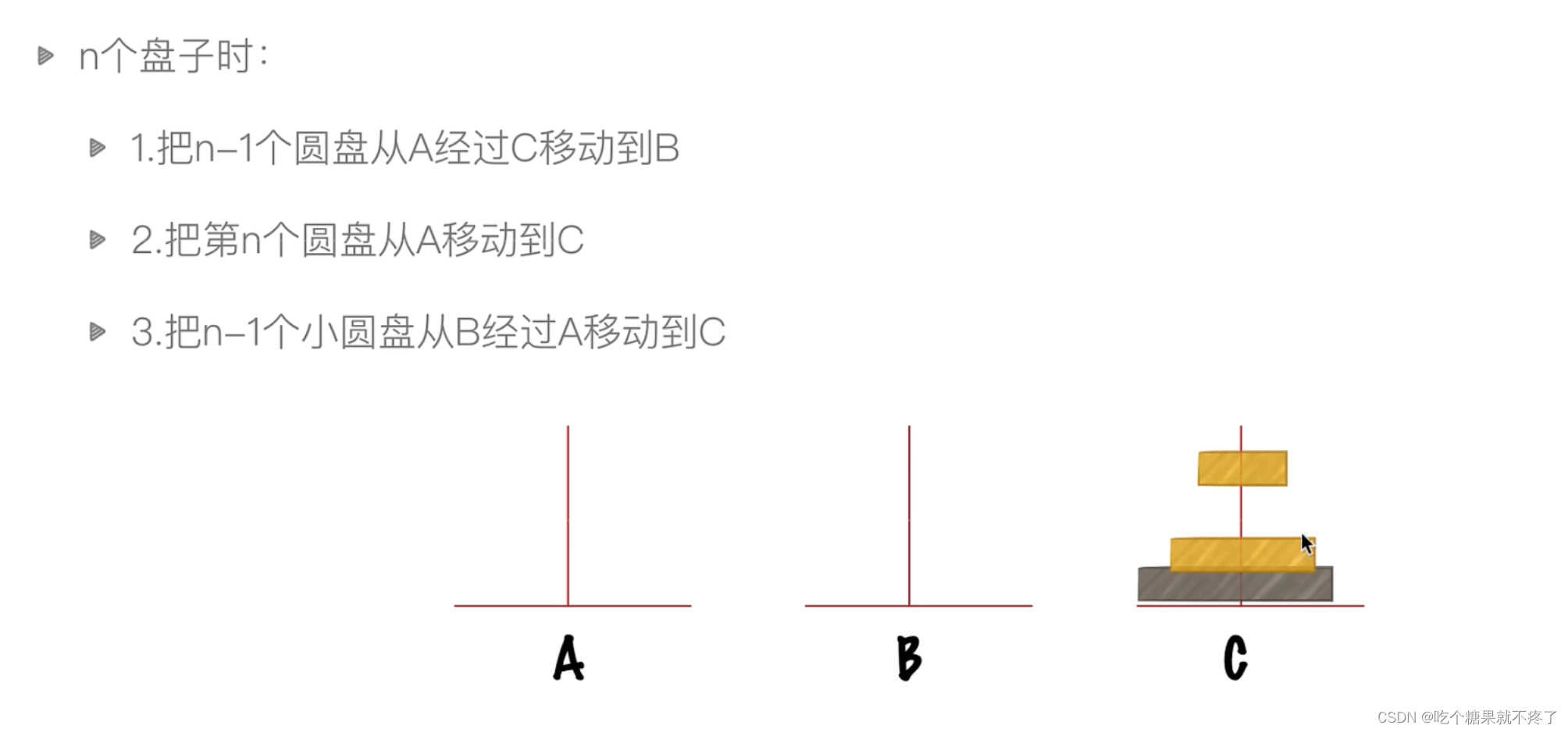
在递归过程中，第2步可以省略，只移动一次不算在递归中，重要的是第一、三步

递归代码

我们省略了移动过程中繁琐的代码，通过递归，让计算机去实现，只需要告诉计算机单个问题时的移动过程，让计算机递归迭代

def hanoi(n,a,b,c):
    if n>0:
        hanoi(n-1,a,c,b)  # a->c->b   # 对应1步
        print("moving from %s to %s"%(a,c)) # 对应2步
        hanoi(n-1,b,a,c)   # 对应3步

hanoi(3,'A','B','C')

结果

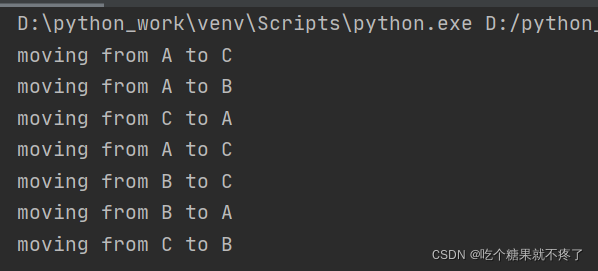
依然是7步，符合验证