首先,我们先来弄明白这个游戏的规则。(已经充分了解的可以跳过这部分)
这里有3个柱子,我们分别称他们为x,y,z,x座上有若干个盘子,盘子大小不等,大的在下,小的在上(如图所示)。
把这些个盘子从x座移到z座,中间可以借用y座但每次只能允许移动一个盘子,并且在移动过程中,3个座上的盘
子始终保持大盘在下,小盘在上。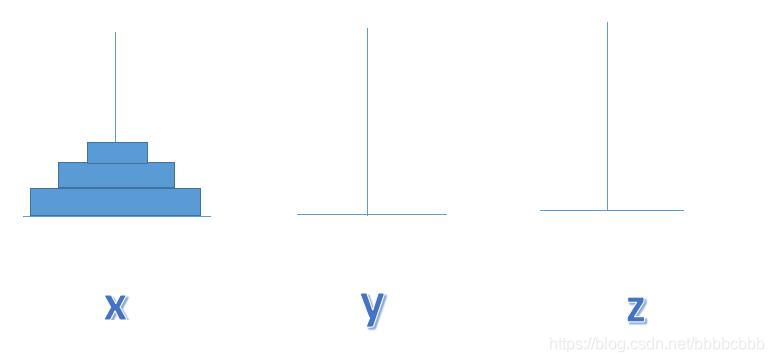
3个盘子就很简单了,(x -> z ,x -> y ,z -> y ,x -> z ,y -> x, y -> z, x -> z)从上到下我们依次叫它们1号2号3号,我们先把1号放在z上,再把2号放在y上,然后把1号放在y上,3号放在z上,1号放在x上,2号放在z上,最后再把1号放在z上就ok了。
现在假设x座上的盘子个数为n,我们要想完成任务就要先把x座上的n-1个盘子移到y上,再把x上的第n个盘子移到z上,最后把y上的n-1个盘子移到z上。对于x上一共有n-1个盘子时也是一样的,先把n-2个盘子移到y上再把第n-1个盘子移到z上,最后再把y上的n-2个盘子移到z上。这样分析问题就好解决了,无非要考虑的就是把盘子通过x移到z上或者是把盘子通过y移到z上。这是迭代法的思想。
下面上代码:
def hanoi(n,x,y,z):#传入形参 n是盘子个数 x,y,z是3个柱子 x位置是起始柱子 y位置是中间商 z位置是最终目标
if n==1: #考虑一个盘子的时候 直接x->z
print(x,’->’,z)
else:
hanoi(n-1,x,z,y)#把n-1个盘子从x移到y上
print(x,’->’,z)
hanoi(n-1,y,x,z)#把n-1个盘子从y移到z上
n =int(input(‘请输入n的值’))
print(hanoi(n,‘x’,‘y’,‘z’))
下面看下n=4时运行结果:
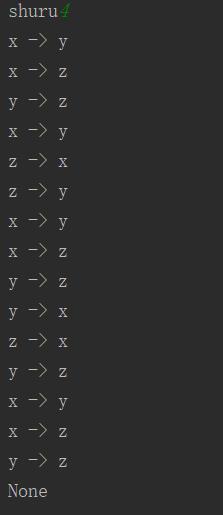
超详细的python递归法解决汉诺塔(hanoi)问题
最新推荐文章于 2024-03-13 23:44:24 发布
 本文详细解析了汉诺塔游戏的规则与玩法,通过递归算法实现了汉诺塔游戏的移动步骤,适用于初学者理解递归思想。
本文详细解析了汉诺塔游戏的规则与玩法,通过递归算法实现了汉诺塔游戏的移动步骤,适用于初学者理解递归思想。




















 1844
1844

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








