简单哈夫曼树的建立,及其编码、译码的详解和实现
基本术语
二叉树的带权路径长度
二叉树中所有叶子结点的带权路径长度之和
根到结点的路径长度
从根到结点的路径上的分支数
哈夫曼树二叉树
又称最优二叉树,是一带权路径长度最短的二叉树。
例:设结点a、b、c、d的权值分别为1、3、5、7,
二叉树(1)的带权路径长度=31+33+25+17=29
二叉树(2)的带权路径长度=21+23+25+27=32
二叉树(3)的带权路径长度=21+33+35+17=33
在所有可以构建的二叉树中,(1)的带权路径长度是最短,所以(1)是最优二叉树。
所以,那么问题来了。
怎么构建哈夫曼树呢?
构建哈夫曼树
算法
-
根据给定的n个权值{w1,w2,…,wn}构成n棵二叉树的集合F={T1,T2,…,Tn},其中每棵二叉树只含一个带权的根结点,其左右子树均空;

-
在F中选两棵根结点的权值最小的二叉树作为左右子树,构造一棵新的二叉树,且置新的二叉树的根结点的权值为其左、右子树上根结点的权值之和;

-
在F中删除这两棵二叉树,同时将新得到的二叉树加入F ;

-
重复2和3,直到F只含一棵二叉树,此即最优二叉树。

代码如下:
//HT为哈夫曼树,MIN为一结构体的命名。
for (int i = num + 1; i <= m; i++)
{
MIN min;
min=Select(HT,i-1);//选择并比较F中两权值最小的两个二叉树
HT[min.s1].parent = i;
HT[min.s2].parent = i;
HT[i].lchild = min.s1;//权值小的二叉树作为新生二叉树的左子树
HT[min.s1].num = "0";
HT[i].rchild = min.s2;//权值大的二叉树作为新生二叉树的右子树
HT[min.s2].num = "1";
HT[i].weight = HT[min.s1].weight + HT[min.s2].weight;//新生的二叉树权值为其左、右子树之和
HT[i].data = -1;
}
译码
输入一串字符,将他们用哈夫曼码的形式输出。
string estring;//创建一个字符串类型的数据,用于存储哈夫曼码
for(int i = 0;i <= s.size(); i++)
{
for(int x = 1; x <= m; x++)
{
if(hft[x].data == s[i])//将所选的字符与哈夫曼树中的字符进行对比
{
estring = estring + hft[x].num;//将哈夫曼码连接起来
x = m;
}
}
}
- 选中要编译字符串中的一个字符;
- 将选中的字符与哈夫曼树中的每个字符进行对比;
- 若两字符相等,则将哈夫曼中字符的哈夫曼码连接至estring(要输出的字符串)后。
- 待要编译的字符串全部编译完成,则输出estring。
解码
输入一串哈夫曼码,将其解码变成一串字符。
string estring;//创建一个字符串类型的数据,用于存储解码得出的字符
int pos = 0, first = 0;
for(int x = 0; x <= s.size(); x++)
{
pos++;
for(int i = 1; i <= m; i++)
{
if(hft[i].num == s.substr(first, pos))//first为从第几个字符开始截取,pos为截取几个字符。
//哈夫曼树中的哈夫曼码与选中的哈夫曼码进行对比
{
cout<<hft[i].data;
first = pos + first;//将字符连接起来
pos = 0;
}
}
}
- 输入一串哈夫曼码;
- 将first指向第一个字符,代表从这个字符开始,pos赋值为1(代表选取一个字符),将选取得到的字符与哈夫曼树中的每个哈夫曼码进行对比;
- 如果两字符相等,将此哈夫曼码相对应的字符直接输出,first 指向pos+first字符处,pos变为1;若不相等,pos+1,接着进行比较。
- 直到译码结束。
这一部分虽然编译成功了,但是思路简单,时间复杂度太大了,资源浪费太多。如果大家有好点的算法或思路,请大家在评论区说一下哦。
完整的代码
#include<iostream>
#include<string>
#include<string.h>
using namespace std;
//哈夫曼树的存储结构
typedef struct
{
char data; //存储数据
int weight; //结点的权重
string num; //存放哈夫曼码
int parent, lchild, rchild; //结点的双亲、左孩子、右孩子的下标
} HTNode,*HuffmanTree;
//两个最小结点
typedef struct
{
int s1;
int s2;
} MIN;
//选择结点权值最小的两个结点
MIN Select(HuffmanTree HT, int n)
{
int min, secmin,s1,s2;
min = 10000;
secmin = 10000;
MIN code;
s1 = 1;
s2 = 1;
for (int i = 1; i <= n; i++)
{
if (HT[i].parent == 0 && (HT[i].weight<min))
{
min = HT[i].weight;
s1 = i;
}
}
for (int i = 1; i <= n; i++)
{
if (HT[i].parent == 0 && (HT[i].weight<secmin) && (i != s1))
{
secmin = HT[i].weight;
s2 = i;
}
}
code.s1 = s1;
code.s2 = s2;
return code;
}
//将哈夫曼码存储在结构体num中
void putlorinnum(HuffmanTree &hft, int num)
{
for(int i = num; i >= 1; i--)
{
if(hft[hft[i].parent].parent)
{
hft[i].num = hft[hft[i].parent].num + hft[i].num;
}
}
}
//创造哈夫曼树
void CreateHuffmanTree(HuffmanTree &HT, int num)
{
int m;
m = 2 * num - 1;
HT = new HTNode[m + 1]; //分配空间
for (int i = 1; i <= m; i++) //初始化
{
HT[i].parent = 0;
HT[i].lchild = 0;
HT[i].rchild = 0;
}
cout << "请输入每个数据及其权值:" << endl;
for (int i = 1; i <= num; i++)
{
cin >> HT[i].weight;
cin>>HT[i].data;
}
for (int i = num + 1; i <= m; i++) //构建哈夫曼树
{
MIN min;
min=Select(HT,i-1); //选择二叉树
HT[min.s1].parent = i;
HT[min.s2].parent = i;
HT[i].lchild = min.s1;
HT[min.s1].num = "0";
HT[i].rchild = min.s2;
HT[min.s2].num = "1";
HT[i].weight = HT[min.s1].weight + HT[min.s2].weight;
HT[i].data = -1;
}
putlorinnum(HT, m);
for (int i = 1; i <= m; i++) //进行每个字符哈夫曼码的输出
{
if(HT[i].data != -1)
{
cout<<HT[i].data<<" 权重为"<<HT[i].weight<<" ,哈夫曼码为:"<<HT[i].num<<endl;
cout<<endl;
}
}
}
//将一串字符编译成哈夫曼码
void changchartohft(HuffmanTree hft, string s, int m)
{
string estring;
for(int i = 0;i <= s.size(); i++)
{
for(int x = 1; x <= m; x++)
{
if(hft[x].data == s[i])//查找哈夫曼树中相应的字符
{
estring = estring + hft[x].num;//哈夫曼码连接起来
x = m;
}
}
}
cout<<estring<<endl;
return;
}
//将一串哈夫曼码解译成一串字符
void changhfttochar(HuffmanTree hft, string s, int m)
{
string estring;
int pos = 0, first = 0;
for(int x = 0; x <= s.size(); x++)
{
pos++;
for(int i = 1; i <= m; i++)
{
if(hft[i].num == s.substr(first, pos))//将截取的字符串和哈夫曼中哈夫曼码近行对比
{
cout<<hft[i].data;
first = pos + first;
pos = 0;
}
}
}
cout<<endl;
}
int main()
{
int num; //结点的个数
string s1, s2;
cout << "请输入哈夫曼树叶子结点的个数:";
cin >> num;
//创造哈夫曼树
HuffmanTree HT;
CreateHuffmanTree(HT, num);
while(1)//设置一个循环,可以选择性进行某些步骤。
{
int q;
cout<<"----------------------"<<endl;
cout<<"编译:1"<<endl;
cout<<"解码:2"<<endl;
cout<<"(其他按键结束)"<<endl;
cout<<"输入要进行的操作:"<<endl;
cin>>q;
if(q==1)
{
cout<<"输入想要编译的一串字符"<<endl;
cin>>s1;
changchartohft(HT, s1, num);
}
else if(q==2)
{
cout<<"输入想要解码的一串数字"<<endl;
cin>>s2;
changhfttochar(HT, s2, num);
}
else
break;
}
return 0;
}
此程序在Code::Blocks上可成功运行。
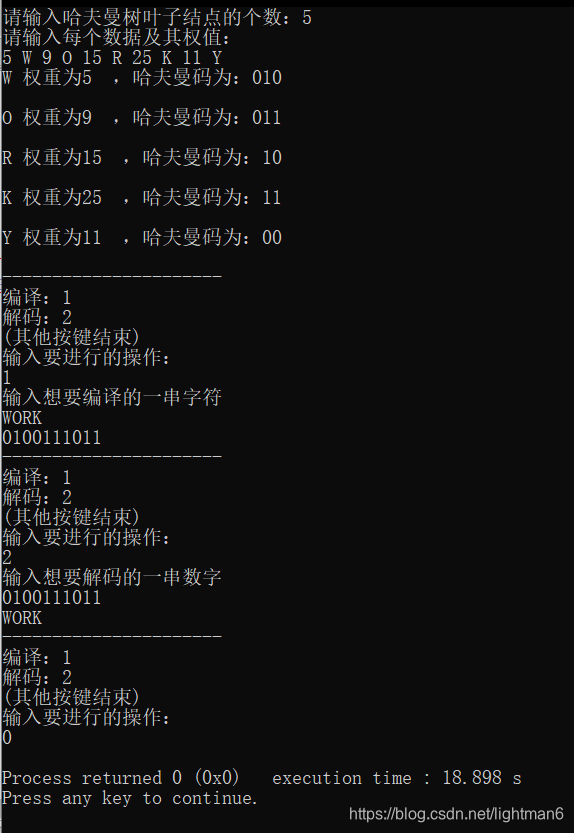
输入输出形式如上图。























 2719
2719

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








