代码随想录算法训练营第 53 天 | 106. 岛屿的周长、110. 字符串接龙、105. 有向图的完全联通

原创 已于 2025-12-08 15:24:30 修改 · 688 阅读 · 8 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#算法 #数据结构 #图 #java

于 2025-12-01 16:54:54 首次发布

106. 岛屿的周长

题目链接

陷阱：虽然是岛屿问题，但是不需要用到任何 dfs 或 bfs

思路：遍历图，如果是陆地，看它上下左右格子是否越界或者为海洋。如果是，周长加 1。

import java.util.*;

public class Main {
    public static int[][] dir = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();

        int[][] grid = new int[n][m];

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                grid[i][j] = sc.nextInt();
            }
        }
        
        int result = 0; // 周长

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (grid[i][j] == 1) {
                    for (int k = 0; k < 4; k++) {
                        int nextX = dir[k][0] + i;
                        int nextY = dir[k][1] + j;
                        
                        // 如果越界或者为海洋，周长就加 1
                        if (nextX < 0 || nextX >= n || nextY < 0 || nextY >= m || grid[nextX][nextY] == 0) {
                            result++;
                        }
                    }
                }
            }
        }

        System.out.println(result);
    }
}

110. 字符串接龙

题目链接

  1. 只由小写字母组成
  2. 不存在路径则输出 0

用 dfs 或 bfs 皆可。但适合用 bfs。因为 bfs 是一圈一圈的，当找到目标字符串时一定是最短路径长度。而 dfs 还要额外保存路径长度去求个最小。

思路：对字符串的每个字符，把它修改为 26 个字母中的每一个字符。判断修改后的字符串在不在字典中。中间一旦变成最终字符串，就返回长度。

需要一个 set 保存字典。
一个 map 保存已经遍历过的字符串。

易错点：
终点字符串不要求在字典中，所以求出 newStr 后要立马判断是不是等于终点字符串

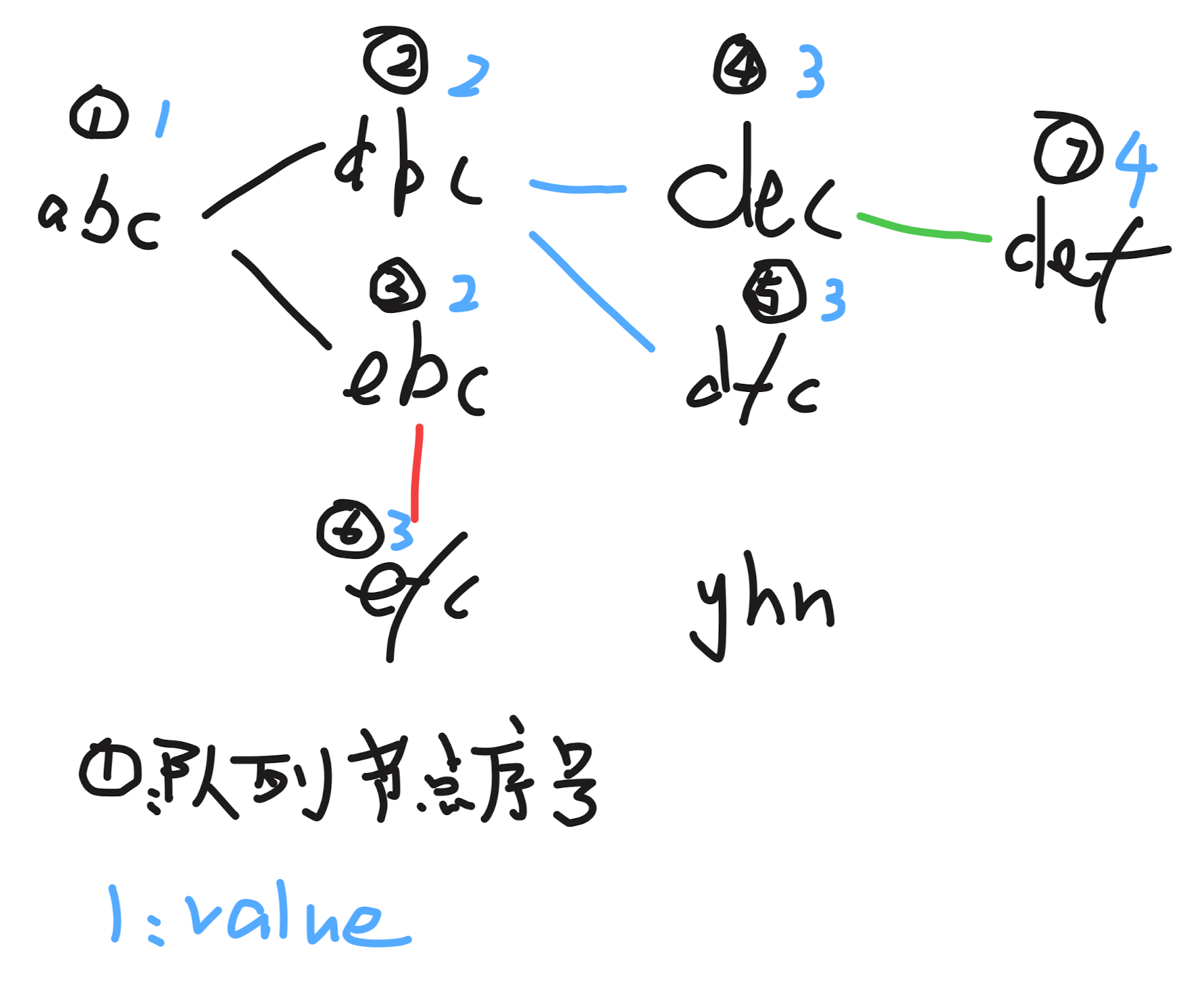
在这里插入图片描述

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();

        String beginStr = sc.next();
        String endStr = sc.next();

        HashSet<String> set = new HashSet<>(); // 保存字典
        for (int i = 0; i < n; i++) {
            set.add(sc.next());
        }

        HashMap<String, Integer> map = new HashMap<>(); // 保存已经遍历过的字符串，value 为当前的路径长度
        Queue<String> queue = new ArrayDeque<>();

        queue.offer(beginStr); // 添加起点字符串
        map.put(beginStr, 1); // 起点字符串路径长度为 1
        
        while (!queue.isEmpty()) {
            String str = queue.poll();
            for (int i = 0; i < str.length(); i++) {
                for (int j = 0; j < 26; j++) {
                    char[] chars = str.toCharArray();
                    chars[i] = (char) ('a' + j);
                    String newStr = new String(chars);

                    // 因为重点字符串不要求出现在字典中，所以需要立即判断是否等于终点字符串，如果是直接输出结果并返回
                    if (newStr.equals(endStr)) {
                        System.out.println(map.get(str) + 1);
                        return;
                    }

                    // 必须字典中包含新字符串，且没有遍历过该新字符串
                    if (!set.contains(newStr) || map.containsKey(newStr)) {
                        continue;
                    }

                    queue.offer(newStr); // 把新字符串添加到队列中
                    map.put(newStr, map.get(str) + 1); // 新字符串路径长度为旧字符串路径长度 + 1

                }
            }
        }

        System.out.println(0); // 遍历完都没找到，输出 0
    }
}

105. 有向图的完全联通

题目链接

读题：共 n 个节点。从节点 1 出发，要能到达每个节点。即判断是不是完全联通图。

dfs 或 bfs 皆可。

思路：
设置一个 visited[] 数组。从节点 1 出发，把它能直接到达的节点都标记为 true。再遍历这些能直接到达的节点。
最后看 visited[] 数组如果有 false，则不是完全联通。

方法一：dfs

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt(); // 节点数量
        int k = sc.nextInt(); // 边数量

        List<List<Integer>> graph = new ArrayList<>(n + 1);
        for (int i = 0; i < n + 1; i++) { // i 必须从 0 开始，创建 n + 1 个空列表
            graph.add(new ArrayList<>());
        }

        while (k-- > 0) {
            int s = sc.nextInt();
            int t = sc.nextInt();
            graph.get(s).add(t);
        }

        boolean[] visited = new boolean[n + 1];

        dfs(graph, 1, visited);

        // 判断 visited[] 中有没有 false
        for (int i = 1; i < n + 1; i++) { // i 从 1 开始
            if (!visited[i]) {
                System.out.println(-1);
                return;
            }
        }
        System.out.println(1);
    }

    public static void dfs (List<List<Integer>> graph, int node, boolean[] visited) {
        if (visited[node]) {
            return;
        }
        visited[node] = true;

        for (int nextNode : graph.get(node)) {
            dfs(graph, nextNode, visited);
        }
    }
}

方法二：bfs

import java.util.*;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt(); // 节点数量
        int k = sc.nextInt(); // 边数量

        List<List<Integer>> graph = new ArrayList<>(n + 1);
        for (int i = 0; i < n + 1; i++) { // i 必须从 0 开始，创建 n + 1 个空列表
            graph.add(new ArrayList<>());
        }

        while (k-- > 0) {
            int s = sc.nextInt();
            int t = sc.nextInt();
            graph.get(s).add(t);
        }

        boolean[] visited = new boolean[n + 1];

        bfs(graph, visited);

        // 判断 visited[] 中有没有 false
        for (int i = 1; i < n + 1; i++) { // i 从 1 开始
            if (!visited[i]) {
                System.out.println(-1);
                return;
            }
        }
        System.out.println(1);
    }

    public static void bfs (List<List<Integer>> graph, boolean[] visited) {
        Queue<Integer> queue = new ArrayDeque<>();
        queue.offer(1);
        visited[1] = true;

        while (!queue.isEmpty()) {
            int node = queue.poll();
            for (int nextNode : graph.get(node)) {
                if (!visited[nextNode]) {
                    queue.offer(nextNode);
                    visited[nextNode] = true;
                }
            }
        }
    }
}

图总结

  • 无权图求最短路径，不需要迪杰特斯拉算法，只需要 dfs 或 bfs 即可。
  • 抽象图用 graph，二维图用 grid。
    • 邻接矩阵用 graph[][]，邻接表用 List<List<Integer>> graph。

邻接矩阵初始化（有向图，节点从 1 到 n）：

import java.util.*;  

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt(); // 节点数量  
        int k = sc.nextInt(); // 边数量  

        int[][] graph = new int[n + 1][n + 1];
        while (k-- > 0) {
            int s = sc.nextInt();
            int t = sc.nextInt();
            graph[s][t] = 1;
        }
    }
}

邻接表初始化（有向图，节点从 1 到 n）：

import java.util.*;  
  
public class Main {  
    public static void main(String[] args) {  
        Scanner sc = new Scanner(System.in);  
        int n = sc.nextInt(); // 节点数量  
        int k = sc.nextInt(); // 边数量  
  
        List<List<Integer>> graph = new ArrayList<>(n + 1);  
        for (int i = 0; i < n + 1; i++) { // i 必须从 0 开始，创建 n + 1 个空列表
            graph.add(new ArrayList<>());  
        }  
  
        while (k-- > 0) {  
            int s = sc.nextInt();  
            int t = sc.nextInt();  
            graph.get(s).add(t);  
        }  
    }  
}
代码随想录算法训练营第三天| 203.移除链表元素 707.设计链表| 206.反转链表
kkksij的博客
10-28 1174
建议： 本题最关键是要理解 虚拟头结点的使用技巧，这个对链表题目很重要。思路：1.直接使用原来的链表进行删除操作。 2.设置一个虚拟头结点在进行删除操作题目链接：. - 力扣（LeetCode）视频链接：手把手带你学会操作链表 | LeetC de：203.移除链表元素_哔哩哔哩_bilibili文章链接：手把手带你学会操作链表 | LeetCode：203.移除链表元素_哔哩哔哩_bilibili具体实现：定义一个cur = head 的结点，遍历链表，每次遍历时 cur.val 和
代码随想录算法训练营第54天|110. 字符串接龙、105.有向图的完全可达性、106. 岛屿的周长
Yinems的博客
08-22 498
同时，本题是个无向图，需要标记节点是否被访问过，不然会陷入死循环，使用集合来检查字符串是否出现在字符串集合中更快一点。用矩阵记录访问过的节点，深搜一遍之后，如果所有节点都被访问过，则输出1。本题是有向图搜索全路径的问题，dfs有两种写法，一种是处理当前访问的节点，如果是访问过的节点则终止本层递归；当走不通时，周长加一。走不通有两种情况，一种是之前访问过，另一种是遇到水域，因此具体为当遇到水域的时候周长加一。有两种解法，一种是遍历每格，遇到岛屿就计算其上下左右的空格情况，如果遇到水域和出界则说明是一条边。
代码随想录算法训练营第54天| 图论 110.字符串接龙 105.有向图的完全可达性 、106.岛屿的周长
meiqiuxiaohei的博客
08-23 455
答案中给的方法是：使用set存储字符串方便查找，然后按26个字母的顺序依次更改当前访问字符串的每一位，每更改一次，则查询一次是否和endStr相等，如果不相等则查找有没有相等的中转字符串，每遍历完一层，count+1。然后再出栈，直到栈空结束。仔细研究了代码，之后再自己写一遍。思路：使用了邻接矩阵和一个布尔数组存储这个点是否被访问过，如果不存在这个点到别的点的路径或者这个点已经被访问过，那么就跳过。在遍历到一个点时，寻找他的四周，如果是边界或者海洋，就+1，如果这个点遍历过或者是海洋或者是边界，就跳过。
代码随想录算法训练营第五八天| 110. 字符串接龙 105.有向图的完全可达性 106. 岛屿的周长
zzhnwpu的博客
10-11 202
105.有向图的完全可达性。110. 字符串接龙。106. 岛屿的周长。
代码随想录算法训练营第五十三天|110.字符串接龙 105.有向图的完全可达性 106.岛屿的周长
aaaaaaaaaaaaay的博客
09-27 105
思路：这道题要找最短的路径，所以使用bfs（如果使用dfs则需要遍历所有路径然后找最短的），将题目提供的list转换为无向图，如果只相差一个字符，则可以连接两个节点。思路：这道题不需要具体的找能否到达某个节点，而是如正常的dfs一样遍历整个地图，看看遍历完后的visit数组是否全是True，是就说明完全可达。思路：这道题不需要使用搜索，简单的遍历并找周围不是陆地的就可以了，不过需要注意超出边界位置没有0或者1，但也要计算为周长。105.有向图的完全可达性。
代码随想录算法训练营第五十二天 |110.字符串接龙 105.有向图的完全可达性 106.岛屿的周长
qq_46651958的博客
03-21 934
给定一个有向图，包含 N 个节点，节点编号分别为 1，2，...，N。现从 1 号节点开始，如果可以从 1 号节点的边可以到达任何节点，则输出 1，否则输出 -1。在搜索的过程中，我们可以枚举，用26个字母替换当前字符串的每一个字符，在看替换后 是否在 strList里出现过，就可以判断 两个字符串 是否是链接的。然后就是求起点和终点的最短路径长度，在无权图中，求最短路，用深搜或者广搜就行，没必要用最短路算法。如果可以从 1 号节点的边可以到达任何节点，则输出 1，否则输出 -1。
代码随想录算法训练营第五十三天 | 110.字符串接龙、105.有向图的完全可达性、106.岛屿的周长
xizhou_sean的博客
08-30 933
如果我们是处理当前访问的节点，当前访问的节点如果是 true ，说明是访问过的节点，那就终止本层递归，如果不是true，我们就把它赋值为true，因为这是我们处理本层递归的节点。首先明确，本题中什么叫做处理，就是 visited数组来记录访问过的节点，该节点默认 数组里元素都是false，把元素标记为true就是处理 本节点了。第一行包含两个正整数，表示节点数量 N 和边的数量 K。我们都知道，有递归就有回溯，回溯就在递归函数的下面， 那么之前我们做的dfs题目，都需要回溯操作，例如：98.所有可达路径，
代码随想录算法训练营第五十三天 | 110.字符串接龙 105.有向图的完全可达性 106.岛屿的周长
decode12的博客
01-19 791
文章链接题目链接：110.字符串接龙。
代码随想录算法训练营第五十九天| 110. 字符串接龙、105. 有向图的完全可达性、106. 岛屿的周长
07-08 1127
从 beginStr 开始, 从左往右替换 beginStr 中的每一个字符, 如果替换后的字符串 word 在 strList 中存在对应的字符串, 说明可以从 beginStr 改变一个字符到达对应的字符串. 使用一个 Map<String, Integer> 记录住到达 word 的路劲长度. 这样不停的遍历, 直到第一次遇到 word.equals(endStr) 则找到了对应的路劲.现从 1 号节点开始，如果可以从 1 号节点的边可以到达任何节点，则输出 1，否则输出 -1。
代码随想录算法训练营第一天 - 704. 二分查找
05-08
代码随想录算法训练营第一天 - 704. 二分查找
代码随想录算法训练营第一天- 977.有序数组的平方 ， 209.长度最小的子数组，59.螺旋矩阵II
10-12
代码随想录算法训练营第一天- 977.有序数组的平方 ， 209.长度最小的子数组，59.螺旋矩阵II
代码随想录算法训练营第六天 -- 字符串1 || 344.反转字符串I / 541.反转字符串II / kamacoder54.替换数字--第八期模拟笔试
2402_83930684的博客
09-08 888
假设n = 3，k = 3，i = 0，第一次是符合的，如果没有等于，那么就不符合，明显不对。我们遍历原字符串，如果原字符串某个字符是字母，那么就在新字符串中最后一个位置填上原来字符串的字母；区间，第 k 个元素的下表是 i + k - 1，那么反转的区间是。如果原来字符串某个字符是数字，那么就在新字符串从后到前依此填上。本道题是要使用双指针，使用相向双指针的方法。首先我们要给原来字符串扩容，这里用到的是。，扩容后新字符串的最后一个字符的索引为。的范围可以到0，它指的是索引下标。这道题是在讲，一个字符串。
欧几里得距离算法-相似度
weixin_45609702的博客
12-04 195
本文介绍了一个计算欧几里得距离的Java方法。该方法接收两个Double数组作为输入，通过计算对应元素差值的平方和再开方，返回两个数组之间的欧几里得距离值。当输入数组长度不一致时，方法会返回0作为默认值。欧几里得距离算法常用于比较两个数组之间的相似度，是数据分析和机器学习中的基础距离度量方法。
练题100天——DAY21：统计奇数个数+合并有序数组
最新发布
2301_81099859的博客
12-07 252
今天写了两道题，难度，并更新了之前的DAY13的冒泡排序+二进制求和、DAY14全排列的思路。
Leetcode 68 搜索插入位置 | 寻找比目标字母大的最小字母
im_AMBER的博客
12-04 1035
你的错误逻辑正确逻辑找到 target 时返回 mid-1找到 target 时，继续向右查找（因为需要「大于」target 的最小字符）target <letters [mid] 时，mid 是候选，需保留，right=mid（左闭右开）或不立即排除 mid循环结束直接返回 letters [0]循环结束后，先判断 left 是否越界：越界则返回 letters [0]，否则返回 letters [left]初始right的取值与「越界判断」不匹配；
C++ ⼀级 2024 年 03 ⽉
weixin_46669997的博客
12-05 35
当 N 为9, 6, 3, 0时，满足条件 N % 3 == 0，因此它们被输出并跟随一个 #。要注意的是，字符串“a+1= ”最后有一个空格，因而输出的内容是：a+1= 2，答案为A。输入21，21%3的结果为0，进入if的分支，因而第4行代码可以被执行。19.【判断题】C++表达式 “10”*2 执行时将报错，因为 “10” 是字符串类型而2是整数类型，它们数据类型不同，不能在一起运算。Cout后面有两个<<，第1个输出字符串5%2=，第2个输出算术运算“5%2”的结果，为1，答案为D。
浅谈：快递物流与算法的相关性（五）
Duoya1105的博客
12-05 163
NP-C 的英文全称是 Non-deterministic Polynomial Complete，即多项式复杂程度的非确定性问题。简单的写法是NP=P？，问题就在这个问号上，到底有没有让NP=P的算法，或是如何证明NP≠P。启发式算法的思想是：在不断解决问题的过程中寻找解决问题的最优方案。再举一个通俗的例子：当我们用数字密码解锁手机时，如果我们不知道密码是多少，必须将所有的数字组合依次尝试。这听起来像是一句废话，如果将它抽象一点的表述，就是：能用电脑快速验证一个解的问题，是否也能够用电脑快速地求出解。
[优选算法专题十.哈希表 ——NO.55~57 两数之和、判定是否互为字符重排、存在重复元素]
2401_83386596的博客
12-03 689
两数之和问题的最优解法采用哈希表实现O(n)时间复杂度，通过存储元素值与下标的映射关系，快速查找互补值。字符重排判定问题通过单哈希数组统计字符出现次数，先加后减并实时校验，确保字符种类和数量完全一致。存在重复元素问题使用哈希集合检测重复元素，遍历数组时检查元素是否已存在于集合中。三种解法均利用哈希结构优化查找效率，将时间复杂度从暴力解法的O(n²)降至O(n)，是典型空间换时间策略的工业级实现。
简单多源BFS问题
MiauwYuki的博客
12-03 192
简单多源BFS问题
代码随想录算法训练营第五天
02-17
### 关于代码随想录算法训练营第五天学习内容 #### 动态规划入门 动态规划是一种通过把原问题分解为相对简单的子问题的方式来求解复杂问题的方法。在第五天的学习中，重点在于理解并掌握动态规划的核心概念及其应用。 #### 解决斐波那契数列问题 斐波那契数列是一个经典的例子来介绍动态规划的思想。对于给定的n值，计算第n项斐波那契数值可以采用自底向上的方法构建解决方案[^1]： ```python def fib(n): if n <= 0: return 0 elif n == 1: return 1 dp = [0] * (n + 1) dp[1] = 1 for i in range(2, n + 1): dp[i] = dp[i - 1] + dp[i - 2] return dp[n] ``` 此实现方式避免了重复计算相同的子问题，从而提高了效率。 #### 攀爬楼梯问题 另一个典型的应用场景是攀爬楼梯问题，假设每次可以选择走一步或两步，则到达第n阶的不同路径总数也可以利用动态规划解决: ```python def climbStairs(n): if n == 1 or n == 2: return n dp = [0] * (n + 1) dp[1], dp[2] = 1, 2 for i in range(3, n + 1): dp[i] = dp[i - 1] + dp[i - 2] return dp[-1] ``` 上述两个案例展示了如何运用动态规划技巧有效地解决问题，并且强调了状态转移方程的重要性以及边界条件处理。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值