实现树的基本功能（层次遍历）

需要掌握：

如何创建树；
树的层次遍历算法。

树是一对多的数据结构

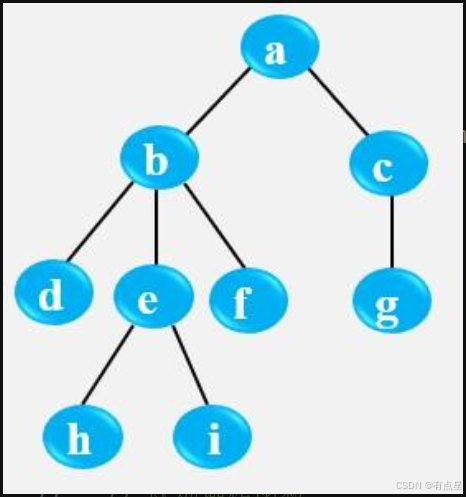
下面给出了一种基于链式存储的实现方案：

#define m 3
typedef char datatype;
typedef struct node {
     datatype data;
     struct node *child[m];
}node, *tree;

#include <iostream>
#include <stdio.h>
#include <stdlib.h>
using namespace std;

#define m 3
#define MAXLEN 100

typedef char datatype;
typedef struct node {
     datatype data;
     struct node *child[m];
} node;
typedef node *tree;

// 队列的定义
typedef struct {
    tree data[MAXLEN];
    int front, rear;
} Queue;

// 队列操作函数
void InitQueue(Queue *q) {
    q->front = q->rear = 0;
}

bool IsEmpty(Queue *q) {
    return q->front == q->rear;
}

bool EnQueue(Queue *q, tree t) {
    if ((q->rear + 1) % MAXLEN == q->front) {
        // 队列已满
        return false;
    }
    q->data[q->rear] = t;
    q->rear = (q->rear + 1) % MAXLEN;
    return true;
}

bool DeQueue(Queue *q, tree *t) {
    if (q->front == q->rear) {
        // 队列为空
        return false;
    }
    *t = q->data[q->front];
    q->front = (q->front + 1) % MAXLEN;
    return true;
}

// LevelOrder函数的实现
void LevelOrder(tree t) {
    Queue q;
    InitQueue(&q); // 初始化队列

    if (t != NULL) {
        EnQueue(&q, t); // 根节点入队

        while (!IsEmpty(&q)) { // 当队列不为空时
            tree node;
            DeQueue(&q, &node); // 出队
            cout << node->data; // 输出当前节点

            // 将当前节点的所有子节点入队
            for (int i = 0; i < m; ++i) {
                if (node->child[i] != NULL) {
                    EnQueue(&q, node->child[i]);
                }
            }
        }
    }
}

// 省略了CreateTree函数的实现...