超级会员免费看
本文介绍了有向无环图(DAG)的拓扑排序，这是一种对事件驱动依赖关系进行排序的方法。文章讨论了两种算法实现：入度表和深度优先搜索(DFS)，并解释了为什么在拓扑排序中顶点必须先于其邻接点出现。两种方法的时间复杂度均为(O(V+E))，并提供了C语言的实现示例。
1. 引言
有向无环图(Directed Acyclic Graph, DAG)是有向图的一种，字面意思的理解就是图中没有环。常常被用来表示事件之间的驱动依赖关系，管理任务之间的调度。拓扑排序是对DAG的顶点进行排序，使得对每一条有向边(u, v)，均有u(在排序记录中)比v先出现。亦可理解为对某点v而言，只有当v的所有源点均出现了，v才能出现。
下图给出有向无环图的拓扑排序：
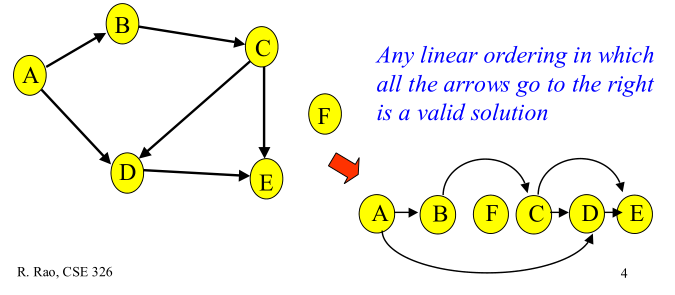
下图给出的顶点排序不是拓扑排序，因为顶点D的邻接点E比其先出现：
2. 算法原理与实现
拓扑排序的实现算法有两种：入度表、DFS，其时间复杂度均为\(O(V+E)\)。
入度表
对于DAG的拓扑排序，显而易见的办法：
- 找出图中0入度的顶点；
- 依次在图中删除这些顶点，删除后再找出0入度的顶点；
- 然后再删除……再找出……
- 直至删除所有顶点，即完成拓扑排序
订阅专栏 解锁全文
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
