Logistic regression(逻辑回归)---deeplearning.ai---笔记及Python源码（13）

一、课程链接

点击打开链接

二、基本理论

（1）模型图：

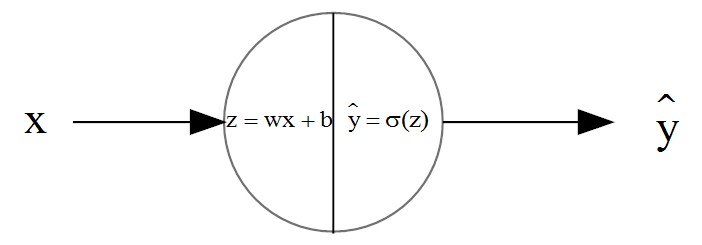
图中所示的为逻辑回归模型，输入为一个一维特征x，输出y hat为预测值。中间神经元的使用了sigmoid函数作为激活函数。那么$$\begin{array}{l}z = wx + b\\\widehat y = \sigma (z) = \frac{1}{{1 + {e^{ - z}}}} \in[0,1]\end{array}$$其中w为权值（weight），b为偏置（bias）。

（2）模型训练准备

在进行模型训练之前，我们已经有很多组训练样本，训练样本指的是多组x，并且对于每个x有相应的y。比如我们需要判断图片中是否有猫这个动物，那么我们再训练之前，已经采集很成千上万张图片（x），并且给这些图片打上有猫（y=1）或者没有猫（y=0）的标签。

那么模型的训练，就是要确定式子中的w和b。如何来确定w和b或者说当有两组不同的w和b的时候，哪一组的w和b更好。这时候，我们引入了损失函数（Loss function）或者称为误差函数（Error function），损失函数在二分类中，可以简单定义为：

$$L(\widehat y,y) = \frac{1}{2}{(y - \widehat y)^2}$$表示通过模型计算的预测输出和实际值的差的平方的一半。这样可以看出当y越接近y hat,L函数越接近0.

但一般使用$$L(\widehat y,y) =  -(ylog(\widehat y) + (1 - y)log(1 - \widehat y))$$这个函数采用最大似然估计的思想。

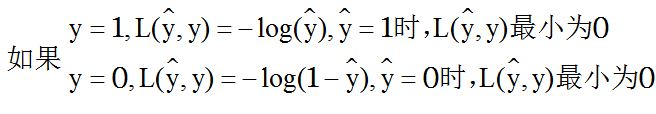
损失函数可以评定单个样本的误差。而对于多个样本就要使用成本函数（cost function）

$$J(w,b) = \frac{1}{m}\sum\limits_{i = 1}^m {L(\widehat y,y)} $$

之所以能够采取求和的方式，具体的推导也是根据最大似然估计得来。而只是一个缩放因子。

（3）梯度下降求解模型参数

定义了成本函数J(w,b)之后，我需要求解在最小化J(w,b)情况下的w和b。当然我们最先想到的就是对进行求导计算。

$$\begin{array}{l}\frac{{\partial J(w,b)}}{{\partial w}} = dw = x(\widehat y - y)\\\frac{{\partial J(w,b)}}{{\partial b}} = db = \widehat y - y\end{array}$$

通过求偏导数，已经计算出梯度，那么使用梯度下降的方法寻找最合适的w和b,采取多次迭代的方式，每次迭代的时候，w和b向梯度下降的方向更新，

$$\begin{array}{l}w = w - \alpha dw\\b = b - \alpha db\end{array}$$从公式中可以看出，当梯度为0，也就是偏导为0的时候，更新的值就为本身，这符合当函数值为极值时，它的导数为0的特征。当然是用梯度下降，如果使用函数非凸，那么很容易陷入极值点，那么从现在的看来，损失函数和成本函数最好为凸函数。

三、向量化逻辑回归及Python源代码实例

所谓向量化，就是在编程中将输入和中间过程的变量采用矩阵或者向量进行表示，减少显示for循环的使用，提高代码执行效率。而在技巧上，尽量使用numpy中的向量或者矩阵处理函数进行，另外还要使用上python中的广播。实际上，如果对matlab熟悉，那么理解这些代码很简单。

设样本的数量为m,每个样本的特征为n_x，那么X可以表示为：$$X = {\left( {\begin{array}{*{20}{c}}{x_1^{(1)}}& \cdots &{x_1^{(m)}}\\ \vdots & \vdots & \vdots \\{x_{n\_x}^{(1)}}& \cdots &{x_{n\_x}^{(m)}}\end{array}} \right)_{n\_x \times m}}$$

输出Y可以表示为$$Y = {\left( \begin{array}{l}{y_1}\\{\rm{ }} \vdots \\{y_m}\end{array} \right)_{m \times 1}}$$

权重W可以表示为$$W = {\left( \begin{array}{l}{w_1}{\rm{ }}\\{\rm{ }} \vdots {\rm{ }}\\{w_{n\_x}}\end{array} \right)_{n\_x \times 1}}$$

b为一个数值非矩阵向量。

所使用的函数都存在numpy，要注意numpy的log和exp函数能够对矩阵进行操作，而math中的exp和log函数对矩阵操作要出现问题。另外使用蓝numpy中的multiply函数，这个函数的作用和matlab中的点乘一样，矩阵中的对应位置的元素相乘。

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Fri Apr 13 17:20:32 2018
logistic regression
@author: sysu-hgavin
"""
import numpy as np
m = 10
n_x = 2
X = np.mat([[1,1],[1.5,1.5],[2,2],[2.5,2.5],[2.75,2.75],[3.15,3.15], \
            [3.5,3.5],[3.75,3.75],[4,4],[4.5,4.5]])#create some examples
X = X.T # transposition
Y = np.mat([[0],[0],[0],[0],[0],[1],[1],[1],[1],[1]])
alpha = 0.01
W = 0.1*np.random.rand(n_x,1)
b = 0
Yhat = np.zeros([m,1])
dW = np.zeros([n_x,1])
dZ = np.zeros([m,1])
db = 0 
j = 0
for iter in range(1000):
    Z = np.dot(W.T,X)+b #
    Yhat = 1/(1+np.exp(-Z))
    dZ = Yhat.T - Y
    dW = 1/m*np.dot(X,dZ)
    db = 1/m*np.sum(dZ)
    #np.multiply is like .* in matlab
    j = -1/m*np.sum(np.multiply(Y.T,np.log(Yhat))+np.multiply((1-Y).T,np.log(1-Yhat)))#
    W = W-alpha*dW
    b = b-alpha*db
print (j)
print ('\n')    
xp = np.mat([[4],[3.5]])
zp = np.dot(W.T,xp)+b
yp = 1/(1+np.exp(-zp))
print (yp)