【LeetCode】嚼烂热题100+浅尝灵神题单【持续更新】

旷野本野

已于 2025-07-08 18:49:33 修改

阅读量972

点赞数 25

CC 4.0 BY-SA版权

文章标签： leetcode 算法

于 2025-04-21 14:55:29 首次发布

本文链接：https://blog.youkuaiyun.com/lidongi/article/details/147247962

1、两数之和

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那两个整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案，并且你不能使用两次相同的元素。

你可以按任意顺序返回答案。

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

package com.example.demo;

import org.springframework.boot.SpringApplication;
import org.springframework.boot.autoconfigure.SpringBootApplication;

import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;

@SpringBootApplication
public class DemoApplication {

    public static void main(String[] args) {

        Scanner sc = new Scanner(System.in);
        System.out.println("请输入个数：");
        int n = sc.nextInt();
        System.out.println("请输入nums的"+n+"个元素");
        int[] nums = new int[n];
        for (int i = 0; i < n; i++) {
            nums[i] = sc.nextInt();
        }
        System.out.println("请输入target：");
        int target = sc.nextInt();
        int[] ans = twoSum(nums,target);
        System.out.print("[");
        for (int i = 0; i < ans.length; i++) {
            if (i == ans.length - 1) {
                System.out.print(ans[i]+"]");
            }else{
                System.out.print(ans[i]+",");
            }
        }

    }
    public static int[] twoSum(int[] nums, int target) {
        Map<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            if (map.containsKey(target - nums[i])) {
                return new int[]{map.get(target - nums[i]), i};
            }
            map.put(nums[i], i);
        }
        return new int[0];
    }

}

2、字母异位词分组

方法一：排序+哈希表

思路：对每个字符串排序，排序后的字符串作为键插入到哈希表中，值为List<String>形式存储单词原型，键为排序后的字符串。

 Map<String, List<String>> m = new HashMap<>();

难点（重点）：

1、排序字符串

字符串本身不能直接排序，需要先利用str.toCharArray()转换成为char[]，再利用Arrays.sort(s)；完成排序，但排序完的s就是char[]形式的。

2、哈希表map已有的接口computeIfAbsent(Key,Function)
map.computeIfAbsent(Key, Function)
若键存在：直接返回对应的值（在本题中返回的就是对应的列表）。
若键不存在：调用 Function 生成新值（本题中就是生成一个空的列表作为新的键对应的值），将键值对存入 Map，并返回新值。

这个方法的平替：但也需要知道map.getOrDefault（）方法
 List<String> list = map.getOrDefault(key, new ArrayList<String>());
 list.add(str);
 map.put(key, list);
值得注意的是：这个Key需要对应map的键值的类型。不能用char[]作为键的类型，因为所有数组类型（如 char[]）继承自 Object，其 hashCode() 和 equals() 基于对象地址（而非内容）。

键可以选用基本类型和部分引用类型：

3、返回值要是List<List<String>>，

Map.values()的返回值是类型为Collection<List<String>>的所有值（List<String>）的集合。要返回List<List<String>>只需要新建一个ArrayList<>（map.values()）即可。

class Solution {
    public List<List<String>> groupAnagrams(String[] strs) {
        Map<String, List<String>> m = new HashMap<>();
        for (String str : strs) {
            char[] s = str.toCharArray();
            Arrays.sort(s);
            // s 相同的字符串分到同一组
            m.computeIfAbsent(new String(s), k -> new ArrayList<>()).add(str);
        }
        return new ArrayList<>(m.values());
    }
}

3、最长连续序列

给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。

请你设计并实现时间复杂度为 O(n) 的算法解决此问题。

输入：nums = [100,4,200,1,3,2]
输出：4
解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。

一个for循环即可实现，设一个count比设left简单，

关键：注意有三种情况——是前一个加一，等于前一个，其他。

class Solution {
    public int longestConsecutive(int[] nums) {

        Arrays.sort(nums);
        int ans = 1;
        int n = nums.length;
        if(n==0){
            return 0;
        }
        int tmp = nums[0];
        int count = 1;
        for(int i = 1;i<n;i++){
            if(nums[i]==tmp+1){
                count++;
                ans = Math.max(ans,count);
                tmp = nums[i];
                continue;
            }else if(nums[i]==tmp){

                continue;
            }else{
                count = 1 ;
                tmp = nums[i];
                ans = Math.max(ans,count);
            }

        }
        return ans;
        
    }
}

4、移动零

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意 ，必须在不复制数组的情况下原地对数组进行操作。

思路：

双指针问题——>left指针指向待填充的位置，依次加1；right指针从小到大依次指向非零的。

相当于右指针每遇到一个非零的数，就把他按照left指针依次存到数组里

class Solution {
    public void moveZeroes(int[] nums) {
        int n = nums.length;
        if(n == 1 || n == 0){
            return;
        }
        int l = 0;
        int r = 0;
        while(r<n){
            if(nums[r] !=0 ){
                int tmp = nums[l];
                nums[l] = nums[r];
                nums[r] = tmp;
                r++;
                l++;
            }else{
                r++;
            }
        }
    }
}

class Solution {
    public void moveZeroes(int[] nums) {
        int n = nums.length;
        int l = 0;
        for(int r = 0 ; r < n ; r++){

            if(nums[r] == 0){
                continue;
            }else if(l != r){
                nums[l] = nums[r];
                nums[r] = 0;
                l++;
            }else {
                l++;
            }
        }    
    }
}

5、盛最多水的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器

示例 1：

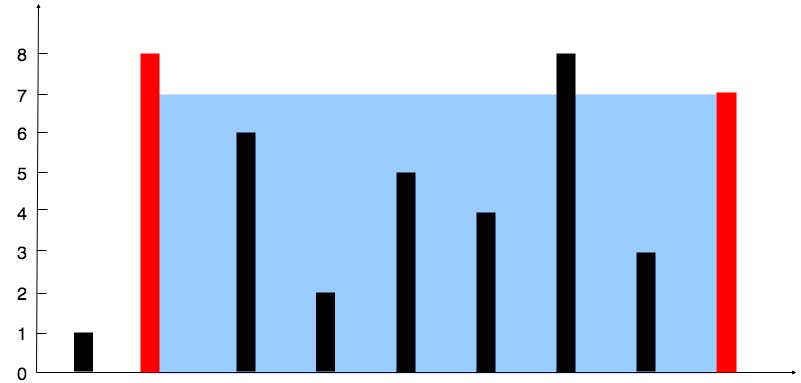
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

思路：

先框到最大，往里缩的时候，肯定是去变化那个最小的边，因为是由于那个边小面积才小的。

class Solution {
    public int maxArea(int[] height) {
        int l = 0;
        int r = height.length-1;
        int ans = 0;
        while(l<r){
             ans = Math.max(ans,(r-l)*Math.min(height[r],height[l]));
            if(height[l]<height[r]){
                l++;
            }else{

                r--;
            }
        }
        return ans;
    }
}

6、三数之和

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

思路：

如果是有序数组，遍历第一个数，则三个数之和相当于在第一个数的右边找两个数和为-nums[i]。

值得注意的是，要避免重复，例如第一个数在遍历的时候就要判断是不是重复了；

后续如果满足了，通过ans.add(List.of(三个数));即可，然后跳过重复的字段。

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        Arrays.sort(nums);
        List<List<Integer>> ans = new ArrayList<>();
        int n = nums.length;
        for (int i = 0; i < n - 2; i++) {
            int x = nums[i];
            if (i > 0 && x == nums[i - 1]) continue; // 跳过重复数字
            if (x + nums[i + 1] + nums[i + 2] > 0) break; // 优化一
            if (x + nums[n - 2] + nums[n - 1] < 0) continue; // 优化二
            int j = i + 1;
            int k = n - 1;
            while (j < k) {
                int s = x + nums[j] + nums[k];
                if (s > 0) {
                    k--;
                } else if (s < 0) {
                    j++;
                } else { // 三数之和为 0
                    ans.add(List.of(x, nums[j], nums[k]));
                    //for (j++; j < k && nums[j] == nums[j - 1]; j++); // 跳过重复数字
                    while(++j < k && nums[j] == nums[j - 1]);
                    //for (k--; k > j && nums[k] == nums[k + 1]; k--); // 跳过重复数字
                    while(--k>j && nums[k] == nums[k+1]);
                }
            }
        }
        return ans;
    }
}

7、接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

思路：

接雨水经典问题：把每一个点当成一个桶，这个点能存多少水取决于他的左右两侧最高值的最小值，否则水会从两边流出去。如果左右两边的最值中相对小的数>这个桶本身的高度，则属于正常接雨水，差值就是接到的雨水。

class Solution {
    public int trap(int[] height) {
        int n = height.length;
        int[] pre = new int[n];
        int[] lst = new int[n];
        pre[0] = height[0];
        lst[n-1] = height[n-1];
        for(int i = 1;i<n;i++){
            pre[i] = Math.max(pre[i-1],height[i]);
        }

        for(int i = n-2 ; i>=0 ;i--){
            lst[i] = Math.max(height[i],lst[i+1]);
        }
        int ans = 0;
        for(int i = 1;i < n-1 ; i++){
            int tmp = Math.min(pre[i],lst[i]);
            if(tmp > height[i]){
                ans+=(tmp-height[i]);
            }
        }
        return ans;
    }
}

8、无重复字符的最长子串

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:

输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

（1）官方得到滑动窗口（更快）

利用哈希表记录每一个字母在滑动窗口中第一次出现的位置。

关键点的是怎么更新哈希表，通过左右指针，判断右指针指向的字符是不是已经存在在哈希表中且在左指针的右边，如果是，就相当于被滑动窗口框住了，也就是说框住的字符串由于右指针的加入，出现了重复的字符，所以要更新左指针和右指针指向的字符在滑动窗口中第一次出现的位置，把左指针指向右指针的字符原本第一次出现的位置+1的位置。

class Solution {
    public int lengthOfLongestSubstring(String s) {
        Map<Character, Integer> map = new HashMap<>();  // 记录字符的最近一次出现位置
        int ans = 0;                                     // 最长子串长度
        int left = 0;                                    // 滑动窗口左边界

        for (int right = 0; right < s.length(); right++) {
            char c = s.charAt(right);
            
            // 关键逻辑：如果字符 c 已经存在，且其位置 >= left，说明它在当前窗口内重复了
            if (map.containsKey(c) && map.get(c) >= left) {
                left = map.get(c) + 1;  // 将左边界移动到重复字符的下一个位置
            }
            
            map.put(c, right);  // 更新字符 c 的最新位置
            ans = Math.max(ans, right - left + 1);  // 计算当前窗口长度，更新最大值
        }
        return ans;
    }
}

（2）我的思路

利用哈希表记录每个字符出现的次数

需要一个公共参数index，判断每次新加的字符是不是已经出现过，如果已经出现过，利用while循环执行把index++指向的字符出现的次数减1，直到新加的字符出现的次数不再大于1。

class Solution {
    public int lengthOfLongestSubstring(String S) {
        Map<Character,Integer> map = new HashMap<>();
        char[] s = S.toCharArray();
        int n = s.length;
        int ans = 0;
        int index = 0;
        for(int i = 0; i<n ; i++){
            if(map.containsKey(s[i])){
                map.put(s[i],map.get(s[i])+1);
            }else{
                map.put(s[i],1);
            }
            if(map.get(s[i])==1){
                ans = Math.max(ans,i-index+1);
            }
            while(map.get(s[i])>1){
                map.put(s[index],map.get(s[index])-1);
                index++;
            }
        }
        return ans;

    }
}

9、找到字符串中所有字母异位词

给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。

示例 1:

输入: s = "cbaebabacd", p = "abc"
输出: [0,6]
解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的异位词。

(1)

标准的定长滑动窗口

关键：（1）利用字符-‘a’ 把字符转换为数字，设 int[ ] cnt = new int[26]

（2）Arrays的一个接口方法：Arrays.equal（数组1，数组2）

（3）滑动窗口三个步骤：入——>更新——>出

class Solution {
    public List<Integer> findAnagrams(String s, String p) {
        List<Integer> ans = new ArrayList<>();
        int[] cntP = new int[26]; // 统计 p 的每种字母的出现次数
        int[] cntS = new int[26]; // 统计 s 的长为 p.length() 的子串 s' 的每种字母的出现次数
        for (char c : p.toCharArray()) {
            cntP[c - 'a']++; // 统计 p 的字母
        }
        for (int right = 0; right < s.length(); right++) {
            cntS[s.charAt(right) - 'a']++; // 右端点字母进入窗口
            int left = right - p.length() + 1;
            if (left < 0) { // 窗口长度不足 p.length()
                continue;
            }
            if (Arrays.equals(cntS, cntP)) { // s' 和 p 的每种字母的出现次数都相同
                ans.add(left); // s' 左端点下标加入答案
            }
            cntS[s.charAt(left) - 'a']--; // 左端点字母离开窗口
        }
        return ans;
    }
}

(2)不定长窗口

class Solution {
    public List<Integer> findAnagrams(String s, String p) {
        List<Integer> ans = new ArrayList<>();
        int[] cnt = new int[26]; // 统计 p 的每种字母的出现次数
        for (char c : p.toCharArray()) {
            cnt[c - 'a']++;
        }
        int left = 0;
        for (int right = 0; right < s.length(); right++) {
            int c = s.charAt(right) - 'a';
            cnt[c]--; // 右端点字母进入窗口
            while (cnt[c] < 0) { // 字母 c 太多了
                cnt[s.charAt(left) - 'a']++; // 左端点字母离开窗口
                left++;
            }
            if (right - left + 1 == p.length()) { // s' 和 p 的每种字母的出现次数都相同
                ans.add(left); // s' 左端点下标加入答案
            }
        }
        return ans;
    }
}

10、和为 K 的子数组

（1）枚举

两个for循环枚举每一个数打头的可能性。

public class Solution {
    public int subarraySum(int[] nums, int k) {
        int count = 0;
        for (int start = 0; start < nums.length; ++start) {
            int sum = 0;
            for (int end = start; end >= 0; --end) {
                sum += nums[end];
                if (sum == k) {
                    count++;
                }
            }
        }
        return count;
    }
}

（2）前缀和优化

枚举的思想是，确定1个开头的数字nums[i]，然后依次求他后面所有数的和；

前缀和的思想：

定义 pre[i] 为 [0..i] 里所有数的和，则 pre[i] 可以由 pre[i−1] 递推而来，即：

pre[i]=pre[i−1]+nums[i]。那么j到i的和就为pre[i]-pre[j-1]，判断是否为k即可。

也就相当于找k+pre[j-1]是否存在

利用哈希表，把前缀和作为键，值为出现的次数。由于是按照从小到大顺序走的，所以出现的次数只会是i之前的和，所以也就相当于遍历了一遍0~i。

public class Solution {
    public int subarraySum(int[] nums, int k) {
        int count = 0, pre = 0;
        HashMap < Integer, Integer > mp = new HashMap < > ();
        mp.put(0, 1);
        for (int i = 0; i < nums.length; i++) {
            pre += nums[i];
            if (mp.containsKey(pre - k)) {
                count += mp.get(pre - k);
            }
            mp.put(pre, mp.getOrDefault(pre, 0) + 1);
        }
        return count;
    }
}

要注意的是：这个key是子串和，值为个数。当pre = k时，不管map里面有没有和为0的，肯定是满足的，所以提前存一个（0,1），处理前缀和直接等于 k 的情况。

11、滑动窗口最大值

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值 。

示例 1：

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

方法一：单调队列

思路：

利用单调队列求：

如果即将进入到框内的数更小，当大的走了这个小的有可能成为最大，但如果即将进来的数比末尾数大，那么这个末尾数就再也不会当做最大值，因为末尾值比即将进来的数小而且走的还早。也就相当于只在队列中保存从大到小的数（单调队列），出现小到大就扔掉小的；

当队列中人数超了，扔掉队首的数，下一个最大的只会是新队首。

主要用到的ArrayDeque<>的方法：

（1）getLast() getFirst();

（2）removeLast()

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        int n = nums.length;
        int[] ans = new int[n - k + 1];
        Deque<Integer> q = new ArrayDeque<>(); // 双端队列
        for (int i = 0; i < n; i++) {
            // 1. 入
            while (!q.isEmpty() && nums[q.getLast()] <= nums[i]) {
                q.removeLast(); // 维护 q 的单调性
            }
            q.addLast(i); // 入队
            // 2. 出
            if (i - q.getFirst() >= k) { // 队首已经离开窗口了
                q.removeFirst();
            }
            // 3. 记录答案
            if (i >= k - 1) {
                // 由于队首到队尾单调递减，所以窗口最大值就是队首
                ans[i - k + 1] = nums[q.getFirst()];
            }
        }
        return ans;
    }
}

（简单看了下，还没理解）方法二优先级队列

我们不断地移除堆顶的元素，直到其确实出现在滑动窗口中。此时，堆顶元素就是滑动窗口中的最大值。为了方便判断堆顶元素与滑动窗口的位置关系，我们可以在优先队列中存储二元组 (num,index)，表示元素 num 在数组中的下标为 index。

算法步骤

初始化优先队列
使用自定义比较器，队列中的元素是包含数值和索引的数组。比较规则：
- 数值降序：数值大的元素优先。
- 索引降序：数值相同时，索引大的元素优先。
```
PriorityQueue<int[]> pq = new PriorityQueue<>(new Comparator<int[]>() {
    public int compare(int[] pair1, int[] pair2) {
        return pair1[0] != pair2[0] ? pair2[0] - pair1[0] : pair2[1] - pair1[1];
    }
});
```

填充初始窗口
将前 k 个元素加入队列：

for (int i = 0; i < k; ++i) {
    pq.offer(new int[]{nums[i], i});
}

处理第一个窗口的最大值
直接取队首元素的值：
```
ans[0] = pq.peek()[0];
```
滑动窗口并更新结果
从第 k 个元素开始遍历：
- 添加新元素到队列。
- 移除过期元素：循环检查队首元素的索引是否在当前窗口的左侧边界之前（即 <= i - k），若过期则弹出。
- 记录当前窗口的最大值。
```
for (int i = k; i < n; ++i) {
    pq.offer(new int[]{nums[i], i});
    while (pq.peek()[1] <= i - k) {
        pq.poll();
    }
    ans[i - k + 1] = pq.peek()[0];
}
```

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        int n = nums.length;
        PriorityQueue<int[]> pq = new PriorityQueue<int[]>(new Comparator<int[]>() {
            public int compare(int[] pair1, int[] pair2) {
                return pair1[0] != pair2[0] ? pair2[0] - pair1[0] : pair2[1] - pair1[1];
            }
        });
        for (int i = 0; i < k; ++i) {
            pq.offer(new int[]{nums[i], i});
        }
        int[] ans = new int[n - k + 1];
        ans[0] = pq.peek()[0];
        for (int i = k; i < n; ++i) {
            pq.offer(new int[]{nums[i], i});
            while (pq.peek()[1] <= i - k) {
                pq.poll();
            }
            ans[i - k + 1] = pq.peek()[0];
        }
        return ans;
    }
}

12、最小覆盖子串

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

注意：

对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串，我们保证它是唯一的答案。

示例 1：

输入：s = "ADOBECODEBANC", t = "ABC"
输出："BANC"
解释：最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。

思路：

遍历右指针，先加进来新的，加进来以后，只要cntS能够覆盖cntT，那么就一直更新返回值，并且更新左指针（左指针加一），直到不再覆盖了。

所以引入了一个方法：能否覆盖？

方法中，可以利用 for（int i = 'A' ; i <= 'Z' ; i++）来遍历（再遍历一遍‘a’到‘z’），只要cntT[i] > cntS[i]，就代表S不覆盖T，就返回false

class Solution {
    public String minWindow(String s, String T) {

        int[] cntS = new int[128];
        int[] cntT = new int[128];
        int n = s.length();
        int ansl = -1;
        int ansr = n;
        for(char t:T.toCharArray()){
            cntT[t] ++;
        }
        int l = 0;
        for(int r = 0 ;r<n;r++){
            cntS[s.charAt(r)]++;
            while(isCoverd(cntS,cntT)){
                if(r-l<ansr-ansl){
                    ansl = l ;
                    ansr = r ;
                }
                cntS[s.charAt(l)]--;
                l++;
            }
            
        }
        return ansl < 0 ? "" : s.substring(ansl,ansr+1);       
    }
    public boolean isCoverd(int[] cntS,int[] cntT){

        for(int i = 'A';i<='Z'; i++ ){
            if(cntS[i]<cntT[i]){
                return false;                         
            }
        }

        for(int i = 'a';i<='z'; i++ ){
            if(cntS[i]<cntT[i]){
                return false;                         
            }
        }
        return true;



    }
}

13、最大子数组和

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

动态规划：

// 定义dp[i] 为以nums[i]结尾的连续子数组的最大和
// 如果dp[i-1]>0,那么 dp[i] = dp[i-1] + nums[i]; 否则，dp[i] = nums[i];
// dp[0] = nums[0];

定义dp[i]很重要，定义不好会南辕北辙。

class Solution {
    public int maxSubArray(int[] nums) {

        int n = nums.length;

        int[] dp = new int[n];
        
        // 定义dp[i] 为以nums[i]结尾的连续子数组的最大和
        // 如果dp[i-1]>0,那么 dp[i] = dp[i-1] + nums[i];  否则，dp[i] = nums[i];
        // dp[0] = nums[0]; 
        int ans = nums[0];
        dp[0] = nums[0];
        for(int i = 1 ; i < n ; i++){
            if(dp[i-1]>0){
                dp[i] = dp[i-1] + nums[i];
            }else{
                dp[i] = nums[i];
            }
            ans = Math.max(ans,dp[i]);

        }
        return ans;
        
    }
}

14、（*）合并区间

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

示例 1：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

先排个序，排序的方法用到了 Lambda表达式

Arrays.sort(intervals, (p, q) -> p[0] - q[0]);

p[0] - q[0]表示按照第一个字符升序排序

排序以后，后面的数组的头肯定不会超过前面数组的头，所以只需要关注后的头与前的尾之间的关系。当ans还是空的或者新的头>ans的尾的尾，那么直接往ans里面加这个新的就好；否则就要更新ans的尾的尾，取ans尾的尾和新的头的最大（因为有可能【1,4】与【2,3】）

返回值要是int[][]型，要利用ans.toArray（new int[ans.size()][]）;

class Solution {
    public int[][] merge(int[][] intervals) {
        Arrays.sort(intervals, (p, q) -> p[0] - q[0]); // 按照左端点从小到大排序
        List<int[]> ans = new ArrayList<>();
        for (int[] p : intervals) {
            int m = ans.size();
            if (m > 0 && p[0] <= ans.get(m - 1)[1]) { // 可以合并
                ans.get(m - 1)[1] = Math.max(ans.get(m - 1)[1], p[1]); // 更新右端点最大值
            } else { // 不相交，无法合并
                ans.add(p); // 新的合并区间
            }
        }
        return ans.toArray(new int[ans.size()][]);
    }
}

15、轮转数组（原地换）

给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

示例 1:

输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]

（1）自己写的

相当于把567提出来，1234后移，再把567放前面。注意1234后移时需要倒序，否则1可能占了4的位置，4就没了

class Solution {
    public void rotate(int[] nums, int k) {

        int n = nums.length;
        k = k%n;
        int[] R = new int[k];
        int index = 0 ;
        for(int i = n-k;i<n;i++){
            R[index++] = nums[i];
        }
        for(int i=n-k-1;i>=0;i-- ){
            nums[i+k] = nums[i];
        }
        for(int i = 0; i < k;i++){
            nums[i] = R[i];
        }
        
    }
}

（2）翻转法

天才！相当于想把1234567翻转，变成7654321，然后再把765和4321分别翻转，就变成了5671234。

class Solution {
    public void rotate(int[] nums, int k) {
        int n = nums.length;
        k %= n; // 轮转 k 次等于轮转 k % n 次
        reverse(nums, 0, n - 1);
        reverse(nums, 0, k - 1);
        reverse(nums, k, n - 1);
    }

    private void reverse(int[] nums, int i, int j) {
        while (i < j) {
            int temp = nums[i];
            nums[i++] = nums[j];
            nums[j--] = temp;
        }
    }
}

16、除自身以外数组的乘积

给你一个整数数组 nums，返回数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。

题目数据保证数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。

请 不要使用除法，且在 O(n) 时间复杂度内完成此题。

示例 1:

输入: nums = [1,2,3,4]
输出: [24,12,8,6]

(1) 我的做法

分别计算i前面的积存储在pre[i]中，i后面的积存储在end[i]中。

那么answer[i] = pre[i] * end[i]；

pre[0] 和 end[n-1]设为1即可。就不会影响其他数值了

class Solution {
    public int[] productExceptSelf(int[] nums) {

        int n = nums.length;
        int[] answer = new int[n];
        int[] pre = new int[n];
        pre[0]=1;
        for(int i = 1 ; i<n ; i++){
            pre[i] = nums[i-1]*pre[i-1];
        }
        int[] end = new int[n];
        end[n-1] = 1;
        for(int i = n-2;i>=0;i--){
            end[i] = end[i+1]*nums[i+1];
        }
        for(int i = 0 ; i < n ; i++){
            answer[i]=pre[i]*end[i];
        }
        return answer;
        
    }
}

17、（*）缺失的第一个正数

给你一个未排序的整数数组 nums ，请你找出其中没有出现的最小的正整数。

请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。

示例 1：

输入：nums = [1,2,0]
输出：3
解释：范围 [1,2] 中的数字都在数组中。

排序的时间复杂度是O(n log n)，超过O(n）了

class Solution {
    public int firstMissingPositive(int[] nums) {
        
        Arrays.sort(nums);
        int ans = 1;
        loop:for(int num:nums){
            if(num<=0){
                continue;
            }else{
                if(num>ans){
                    break loop;
                }else{
                    ans=num+1;
                }
            }
        }
        return ans; 
    }
}

天才！

思路：

把1~n的数字放到对应的i-1位置处，其余不是1~n的数字或者是重复了的数字就被填补到其他位置

具体：

他要找不存在的最小正整数，就是从1-n+1里面找，其他的数可以直接忽略

从前往后遍历，如果nums[i]是1-n的数，并且nums[i] ！= nums[nums[i]-1]（如果一样的话就是重复数字，不用换，nums[i]就是需要忽略的数字了），

把大小在【1，n】的nums[i]放到第nums[i]-1个的位置（因为这个数组是从0-n-1编号的），而且被换过去的数成为了新的nums[i]，还要继续对nums[i]执行同样的操作，直到nums[i]的值不是1-n的数了或者 nums[i]的值跟nums[nums[i]-1]是一样的（这样就考虑到了重复的数字），就可以继续遍历了。

这样的话，1应该放在nums[0]，以此类推....而不属于1-n的数，就被放在了缺少的1-n的数的位置，

那么只要找到第一个nums[i]！=i+1的数，就是要找的不存在的最小正整数，直接return。

如果没有return，说明全部nums[i] == i+1，那么ans直接就是n+1就对了。

class Solution {
    public int firstMissingPositive(int[] nums) {
        
        int n = nums.length;
        for(int i = 0 ; i<n ; i++){
            while(1<=nums[i] && nums[i]<=n && nums[i]!=nums[nums[i]-1]){
                int tmp = nums[nums[i]-1];
                nums[nums[i]-1] = nums[i];
                nums[i] = tmp;
            }
        }
        for(int i = 0 ; i < n ; i++){
            if(nums[i]!=i+1){
                return i+1;
            }
        }
        return n+1;
        
    }
}

18、矩阵置零

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用原地算法。

示例 1：

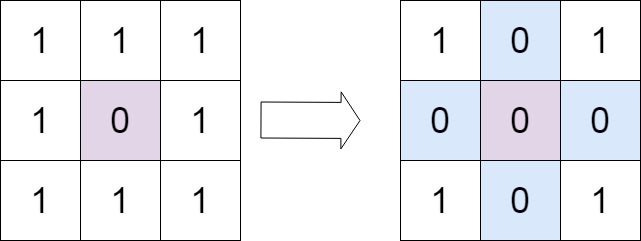
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

22、相交链表

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

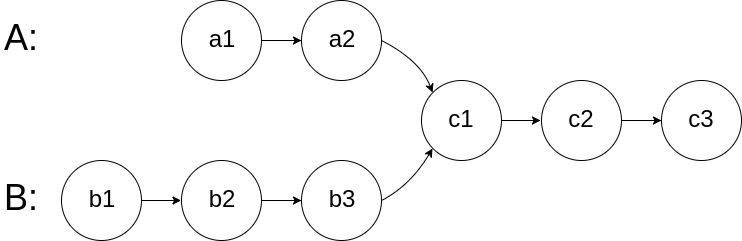
图示两个链表在节点 c1 开始相交：

题目数据保证整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

自定义评测：

评测系统 的输入如下（你设计的程序 不适用 此输入）：

intersectVal - 相交的起始节点的值。如果不存在相交节点，这一值为 0
listA - 第一个链表
listB - 第二个链表
skipA - 在 listA 中（从头节点开始）跳到交叉节点的节点数
skipB - 在 listB 中（从头节点开始）跳到交叉节点的节点数

评测系统将根据这些输入创建链式数据结构，并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点，那么你的解决方案将被 视作正确答案 。

示例 1：

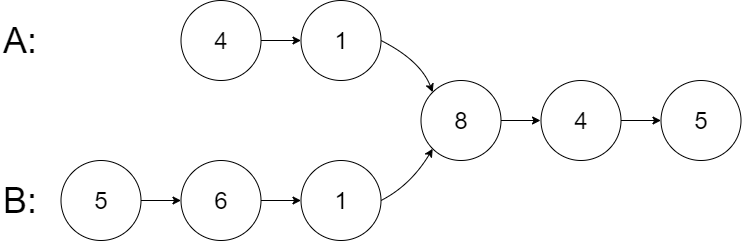
输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出：Intersected at '8'
解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,6,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。
— 请注意相交节点的值不为 1，因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说，它们在内存中指向两个不同的位置，而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点，B 中第四个节点) 在内存中指向相同的位置。

what can i say? 天才！

思路：

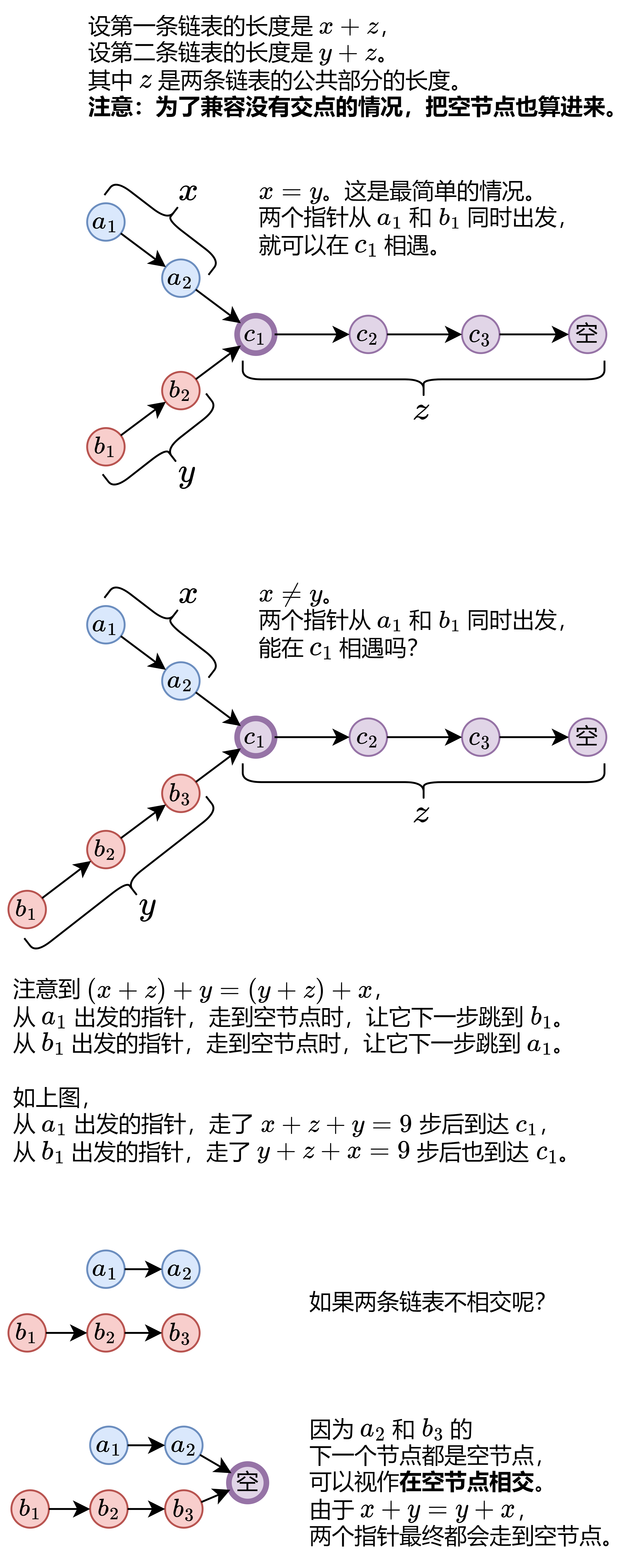
如下图所示，类似于追逐问题，俩人都是一次走一步，要想相遇到同一个点，移动的次数还一样，只需要跑完自己的x+z后再跑y，就能与跑完自己的y+z后再跑x的另一个点相遇在交点处。

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode p = headA;
        ListNode q = headB;
        while(p!=q){
            p = p!=null?p.next:headB;
            q = q!=null?q.next:headA;
        }
        return q;
    }
}

23、反转链表

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

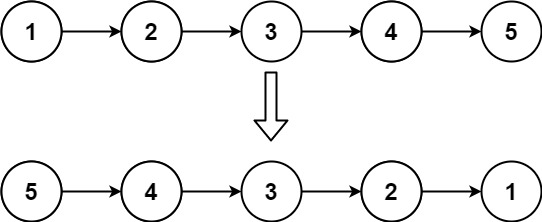
输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

两种方法：（1）迭代（2）递归

（1）迭代

好像也没什么可说的，先获取当前的下一个节点next，把当前的指向前一个节点，当前节点就是新的prev，curr就是之前存的next。

class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode prev = null;
        ListNode curr = head;
        while (curr != null) {
            ListNode next = curr.next;
            curr.next = prev;
            prev = curr;
            curr = next;
        }
        return prev;
    }
}

（2）递归

    /**
     * 以链表1->2->3->4->5举例
     * @param head
     * @return
     */
    public ListNode reverseList(ListNode head) {
        if (head == null || head.next == null) {
            /*
                直到当前节点的下一个节点为空时返回当前节点
                由于5没有下一个节点了，所以此处返回节点5
             */
            return head;
        }
        //递归传入下一个节点，目的是为了到达最后一个节点
        ListNode newHead = reverseList(head.next);
                /*
            第一轮出栈，head为5，head.next为空，返回5
            第二轮出栈，head为4，head.next为5，执行head.next.next=head也就是5.next=4，
                      把当前节点的子节点的子节点指向当前节点
                      此时链表为1->2->3->4<->5，由于4与5互相指向，所以此处要断开4.next=null
                      此时链表为1->2->3->4<-5
                      返回节点5
            第三轮出栈，head为3，head.next为4，执行head.next.next=head也就是4.next=3，
                      此时链表为1->2->3<->4<-5，由于3与4互相指向，所以此处要断开3.next=null
                      此时链表为1->2->3<-4<-5
                      返回节点5
            第四轮出栈，head为2，head.next为3，执行head.next.next=head也就是3.next=2，
                      此时链表为1->2<->3<-4<-5，由于2与3互相指向，所以此处要断开2.next=null
                      此时链表为1->2<-3<-4<-5
                      返回节点5
            第五轮出栈，head为1，head.next为2，执行head.next.next=head也就是2.next=1，
                      此时链表为1<->2<-3<-4<-5，由于1与2互相指向，所以此处要断开1.next=null
                      此时链表为1<-2<-3<-4<-5
                      返回节点5
            出栈完成，最终头节点5->4->3->2->1
         */
        head.next.next = head;
        head.next = null;
        return newHead;
    }

24、（*）回文链表

给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true ；否则，返回 false 。

示例 1：

输入：head = [1,2,2,1]
输出：true

(1) 寻找链表中间节点+ 翻转链表

思路：
找到中间节点，翻转中间节点之后的链表。拿这个新链表和旧链表比较

涉及到

876. 链表的中间结点，视频讲解【基础算法精讲 07】

给你单链表的头结点 head ，请你找出并返回链表的中间结点。

如果有两个中间结点，则返回第二个中间结点。

示例 1：
输入：head = [1,2,3,4,5]
输出：[3,4,5]
解释：链表只有一个中间结点，值为 3 。
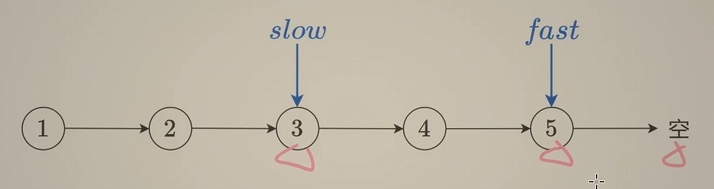
快慢指针：慢指针一步一步走，快指针两步两步走，那么快指针到末尾的时候，慢指针就在中间。当快指针指向空，或者快指针的下一个指向空，慢指针就指向中间

快指针是两步两步走的，快指针指向的一定是第奇数个，所以说，如果整个链表是奇数的，他就会指向最后一个，他的下一个是null；如果整个链表是偶数的，他会直接指向null。

所以只要fast指向了null或者fast的next是null，slow就在中间
class Solution {
    public ListNode middleNode(ListNode head) {

        ListNode slow = head;
        ListNode fast = head;
        while(fast!=null && fast.next!=null){
            slow = slow.next;
            fast = fast.next.next;
        }
        return slow;
        
    }
}

206. 反转链表，视频讲解【基础算法精讲 06】

class Solution {
    public boolean isPalindrome(ListNode head) {
        ListNode mid = middle(head);
        ListNode newHead = reverse(mid);
        while(newHead!=null){
            if(head.val != newHead.val){
                return false;
            }
            head = head.next;
            newHead = newHead.next;

        }
        return true;
    }
    public ListNode reverse(ListNode head){
        ListNode cur = head;
        ListNode pre = null;
        while(cur!=null){
            ListNode next = cur.next;
            cur.next = pre;
            pre = cur;
            cur = next;
        }
        return pre;

    }
    public ListNode middle(ListNode head){
        ListNode fast = head;
        ListNode slow = head;
        while(fast!=null && fast.next!=null){
            slow = slow.next;
            fast = fast.next.next;
        }
        return slow;

    }
}

25、环形链表

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。

如果链表中存在环 ，则返回 true 。否则，返回 false 。

示例 1：

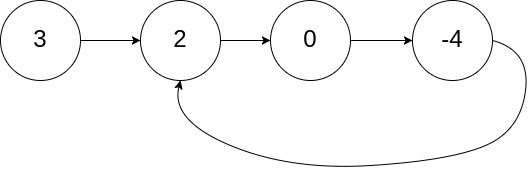
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

（1）利用ArrayList的contains方法

public class Solution {
    public boolean hasCycle(ListNode head) {
        ArrayList<ListNode> list  = new ArrayList<ListNode>();
        while(head!=null){
            if(list.contains(head.next)){
                return true;
            }
            list.add(head);
            head = head.next;
        }
        return false;

        
    }
}

（2）快慢指针法

天才！

如果快指针等于慢指针了，说明有环

public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode fast = head;
        ListNode slow = head;
        while(fast!=null && fast.next!=null  ){
            fast = fast.next.next;
            slow = slow.next;
            if(fast==slow){
                return true;
            }
        }
        return false;
        
    }
}

26、环形链表 II

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：

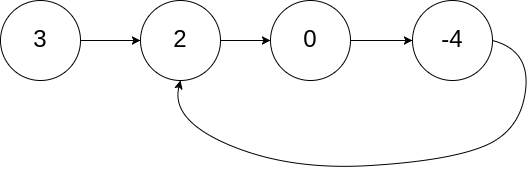
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

（1）ArrayList的contains

public class Solution {
    public ListNode detectCycle(ListNode head) {

        ArrayList<ListNode> list  = new ArrayList<ListNode>();
        while(head!=null){
            if(list.contains(head.next)){
                return head.next;
            }
            list.add(head);
            head = head.next;
        }
        return null;
        
    }
}

（2）快慢指针

【环形链表II【基础算法精讲 07】】

个人感觉，虽然天才，但是不是面试的时候能推出来的。

27、合并两个有序链表

将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例 1：

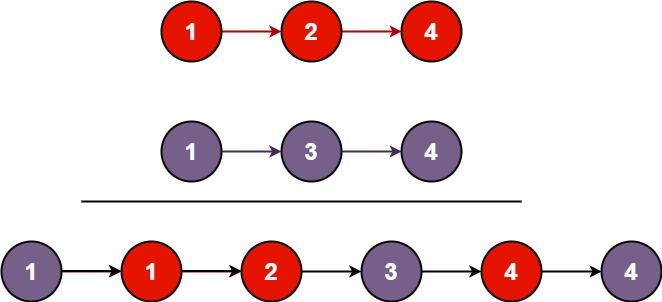
输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

迭代思想：
关键点——>
ListNode prehead = new ListNode(-1); // 哑节点
建立哑结点，就不需要给节点赋初值了，直接适用head.next = 啥就行，否则本题需要讨论头结点是谁。

要留存头结点（返回时要用），赋next的值的时候，要额外设一个节点=head节点

class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        ListNode prehead = new ListNode(-1);

        ListNode prev = prehead;
        while (l1 != null && l2 != null) {
            if (l1.val <= l2.val) {
                prev.next = l1;
                l1 = l1.next;
            } else {
                prev.next = l2;
                l2 = l2.next;
            }
            prev = prev.next;
        }

        // 合并后 l1 和 l2 最多只有一个还未被合并完，我们直接将链表末尾指向未合并完的链表即可
        prev.next = l1 == null ? l2 : l1;

        return prehead.next;
    }
}

28、两数相加

给你两个非空的链表，表示两个非负的整数。它们每位数字都是按照逆序的方式存储的，并且每个节点只能存储一位数字。

请你将两个数相加，并以相同形式返回一个表示和的链表。

你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

示例 1：

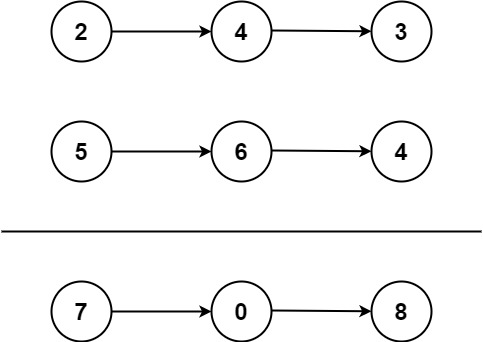
输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.

分开谈论了 l1 l2是否为null

class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {

        int tmp = 0;
        ListNode head = new ListNode(-1);
        ListNode pre = head;
        while(l1!=null || l2!=null || tmp!=0 ){
            if(l1 != null){
                tmp +=l1.val;
                l1 = l1.next;
            }
            if(l2 != null){
                tmp +=l2.val;
                l2 = l2.next;
            }
            pre.next = new ListNode(tmp %10);
            pre = pre.next;
            tmp /=10;
        }
        return head.next;
    }
}

29、删除链表的倒数第 N 个结点

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

示例 1：

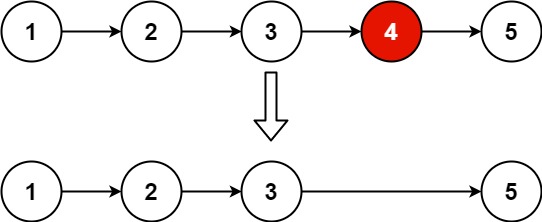
输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

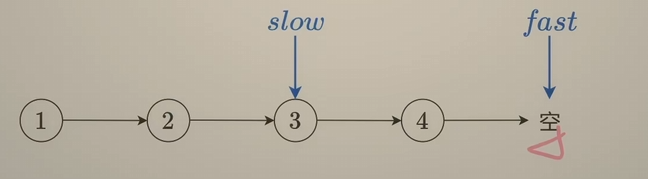
双指针，左右指针差n，右指针到达末尾的时候，左指针指向的是要删去的点的前一个。

class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {

        ListNode dummy = new ListNode(0,head);
        ListNode left = dummy;
        ListNode right = dummy;
        while(n-- > 0){
            right = right.next;
        }
        while(right.next!=null){
            left = left.next;
            right = right.next;
        }
        left.next = left.next.next;
        return dummy.next;

        
    }
}

class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {
        ListNode dummy = new ListNode(0, head);
        int length = getLength(head);
        ListNode cur = dummy;
        for (int i = 1; i < length - n + 1; ++i) {
            cur = cur.next;
        }
        cur.next = cur.next.next;
        ListNode ans = dummy.next;
        return ans;
    }

    public int getLength(ListNode head) {
        int length = 0;
        while (head != null) {
            ++length;
            head = head.next;
        }
        return length;
    }
}

30、两两交换链表中的节点

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

示例 1：

输入：head = [1,2,3,4]
输出：[2,1,4,3]

递归！无他，唯手熟尔

class Solution {
    public ListNode swapPairs(ListNode head) {
        if(head == null || head.next == null){
            return head;
        }
    
        ListNode node = swapPairs(head.next.next);
        ListNode tmp = head.next;
        head.next = node;
        tmp.next = head;
        return tmp;
    }
}

31、K 个一组翻转链表

给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

示例 1：

输入：head = [1,2,3,4,5], k = 2
输出：[2,1,4,3,5]

class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
        ListNode hair = new ListNode(0);
        hair.next = head;
        ListNode pre = hair;

        while (head != null) {
            ListNode tail = pre;
            // 查看剩余部分长度是否大于等于 k
            for (int i = 0; i < k; ++i) {
                tail = tail.next;
                if (tail == null) {
                    return hair.next;
                }
            }
            ListNode nex = tail.next;
            ListNode[] reverse = myReverse(head, tail);
            head = reverse[0];
            tail = reverse[1];
            // 把子链表重新接回原链表
            pre.next = head;
            tail.next = nex;
            pre = tail;
            head = tail.next;
        }

        return hair.next;
    }

    public ListNode[] myReverse(ListNode head, ListNode tail) {
        ListNode prev = tail.next;
        ListNode p = head;
        while (prev != tail) {
            ListNode nex = p.next;
            p.next = prev;
            prev = p;
            p = nex;
        }
        return new ListNode[]{tail, head};
    }
}

迭代，判断当前有没有k个，有的话就对当前的翻转，然后连接翻转后的后面节点。如果没有k个，

class Solution {
    public ListNode reverseKGroup(ListNode head, int k) {
        // 检查剩余节点是否足够k个
        ListNode curr = head;
        int count = 0;
        while (count < k && curr != null) {
            curr = curr.next;
            count++;
        }
        
        // 如果足够k个，则反转当前组并递归处理后续
        if (count == k) {
            ListNode reversedHead = reverse(head, k); // 反转当前k个节点
            head.next = reverseKGroup(curr, k);       // 原头节点连接后续结果
            return reversedHead;
        }
        // 不足k个则直接返回
        return head;
    }
    
    // 迭代反转前k个节点
    private ListNode reverse(ListNode head, int k) {
        ListNode prev = null;
        ListNode curr = head;
        while (k-- > 0) {
            ListNode next = curr.next;
            curr.next = prev;
            prev = curr;
            curr = next;
        }
        return prev;
    }
}

32、随机链表的复制

给你一个长度为 n 的链表，每个节点包含一个额外增加的随机指针 random ，该指针可以指向链表中的任何节点或空节点。

构造这个链表的 深拷贝。深拷贝应该正好由 n 个全新节点组成，其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点，并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。

例如，如果原链表中有 X 和 Y 两个节点，其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ，同样有 x.random --> y 。

返回复制链表的头节点。

用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示：

val：一个表示 Node.val 的整数。
random_index：随机指针指向的节点索引（范围从 0 到 n-1）；如果不指向任何节点，则为 null 。

你的代码只接受原链表的头节点 head 作为传入参数。

示例 1：

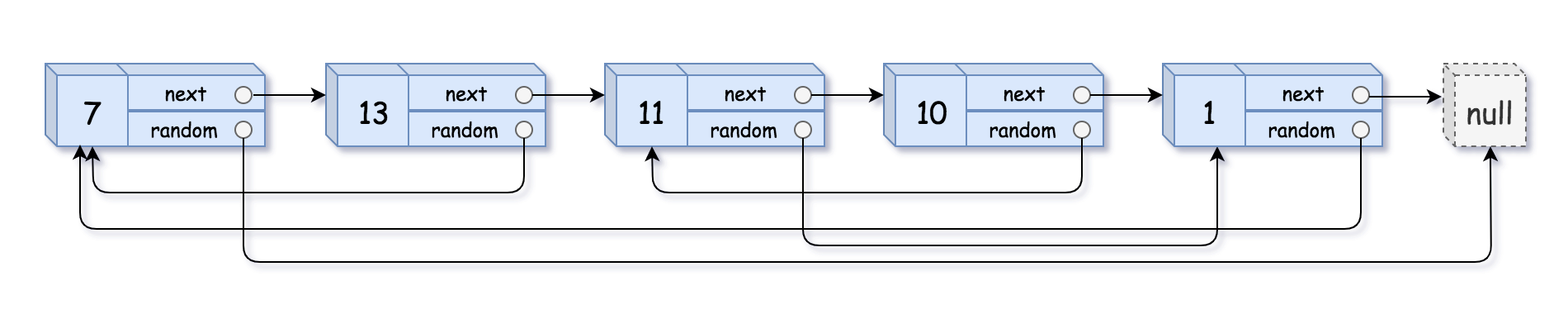
输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

33、排序链表

给你链表的头结点 head ，请将其按升序排列并返回 排序后的链表 。

示例 1：

输入：head = [4,2,1,3]
输出：[1,2,3,4]

利用ArrayList+Collections.sort(list，（s1,s2）-> (s1.val - s2.val))

需要注意的点：存放到list中时，要把next关系都拆了，要不然后面连会很乱。node先赋值它的下一个节点，再把no的next设为null，再存到list里面。

class Solution {
    public ListNode sortList(ListNode head) {
        ListNode ans = new ListNode(0);
        ListNode a = ans;
        ArrayList<ListNode> list = new ArrayList<>();
        ListNode node = head;
        while(node!=null){
            ListNode no = node;
            node = node.next;
            no.next = null;
            list.add(no);
            
        }
        Collections.sort(list,(s1,s2)->(s1.val-s2.val));
        for(ListNode n :list){
            ans.next = n;
            ans = ans.next;
        }
        return a.next;

    }
}

34、合并 K 个升序链表

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：

输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
  1->4->5,
  1->3->4,
  2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

class Solution {
    public ListNode mergeKLists(ListNode[] lists) {

        ArrayList<ListNode> arr = new ArrayList<>();

        for(ListNode list :lists){

            while(list!=null){
                ListNode add = list;
                list = list.next;
                add.next = null;
                arr.add(add);
            }

        }
        Collections.sort(arr,(s1,s2)->(s1.val-s2.val));
        ListNode dummy = new ListNode(0);
        ListNode head = dummy;
        for(ListNode node:arr){
            head.next = node;
            head = head.next;
        }
        return dummy.next;
        
    }
}

35、LRU 缓存

请你设计并实现一个满足 LRU (最近最少使用) 缓存约束的数据结构。

实现 LRUCache 类：

LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该逐出最久未使用的关键字。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

class LRUCache {
    public static class Node{
        int key,value;
        Node prev,next;
        Node(int k , int v){
            key = k;
            value = v;
        }
    }

    private final int capacity;
    private final Node dummy = new Node(0,0);
    private final Map<Integer,Node> keyToNode = new HashMap<>();

    public LRUCache(int capacity) {
        this.capacity = capacity;
        dummy.next = dummy;
        dummy.prev = dummy;
    }
    
    public int get(int key) {
        Node node = getNode(key);
        return node != null? node.value:-1;
    }
    
    public void put(int key, int value) {

        Node node = getNode(key);
        if(node != null){
            node.value = value;
            return;
        }
        node = new Node(key,value);
        keyToNode.put(key,node);
        pushF(node);
        if(keyToNode.size()>capacity){
            Node back = dummy.prev;
            remove(back);
            keyToNode.remove(back.key);
        }

        
    }
    public Node getNode(int key){
        if(!keyToNode.containsKey(key)){
            return null;
        }
        Node node = keyToNode.get(key);
        remove(node);
        pushF(node);
        return node;
    }
    public void remove(Node x){
        x.prev.next = x.next;
        x.next.prev = x.prev;
    }
    public void pushF(Node x){
        x.next = dummy.next;
        x.prev = dummy;
        dummy.next = x;
        x.next.prev = x;
    }

}

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache obj = new LRUCache(capacity);
 * int param_1 = obj.get(key);
 * obj.put(key,value);
 */

36、

完全平方数

给你一个整数 n ，返回 和为 n 的完全平方数的最少数量 。

完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

示例 1：

输入：n = 12
输出：3 
解释：12 = 4 + 4 + 4

动态规划+递推：
f[i]表示的是和为i用到的最少数字个数

其中递推时，f【i】= 最小的一个f[i-j*j]+1；

要注意的是：i要从1开始遍历，不要从0开始，dp【0】本来自然的就是0，遍历以后dp【0】会变成很大的值。

class Solution {
    public int numSquares(int n) {
        // 

        int[] f = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            int minn = Integer.MAX_VALUE;
            for (int j = 1; j * j <= i; j++) {
                minn = Math.min(minn, f[i - j * j]);
            }
            f[i] = minn + 1;
        }
        return f[n];
    }
}

零钱兑换

给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的。

示例 1：

输入：coins = [1, 2, 5], amount = 11
输出：3 
解释：11 = 5 + 5 + 1

dp[i] 表示组成面额为i的可能的组合数

递推公式为：dp【i】 = 最小的dp【i-nums【j】】+1；

关键点：如果要找的i-nums【j】不存在，按照程序，dp【i-nums【j】】已经是很大的值了。所以要先判断dp【i-nums【j】】他是不是小于min，小于的话才是有用的值

class Solution {
    public int coinChange(int[] coins, int amount) {
        int n = coins.length;
        int[] dp = new int[amount+1];
        dp[0] = 0;
        if(amount == 0 ){return 0;}
        // dp[i] 表示面额和为i的最少硬币个数
        // dp[i] = min( dp[i-coins[j]] ) +1;
        for(int i = 1 ; i<amount+1 ; i++){
            int min = Integer.MAX_VALUE;
            for(int j = 0 ; j<n  ;j++ ){
                if(coins[j] <= i && dp[i-coins[j]]<min){
                    min = dp[i-coins[j]]+1;}
                
            }
            dp[i] = min ;
        }
        return dp[amount]>amount ?-1:dp[amount];
    }
}

单词拆分

给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。

注意：不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。

示例 1：

输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。

动态规划： dp【i】表示前i个字符能不能被表示，dp【0】=true。如果i前面有j，使得dp【j】= true的同时，后面的字段能在s中找到。

class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        int n = s.length();
        boolean[] dp = new boolean[n+1];
        dp[0] = true;
        for(int i = 1 ; i<n+1 ; i++){
            for(int j = 0 ; j<i ; j++){

                if(dp[j] && wordDict.contains(s.substring(j,i)) ){
                    dp[i] = true;
                }

            }
        }
        return dp[n];
        
    }
}

最长递增子序列

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例 1：

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

动态规划+递推：

dp【i】表示前i个数字里面最长的子序列长度，

遍历i前面的，如果nums[j]<nums[i]，那么也就是说，nums【i】可以拼到以j结尾的最大序列里面。那j可能有多个，要选出使得dp[i]最大的，所以dp[i] = Math.max(dp[i],dp[j]+1);
最后的ans取dp[i]里面的最大的即可。

class Solution {
    public int lengthOfLIS(int[] nums) {
  
        int n = nums.length;
        int ans= 0 ;
        int[] dp = new int[n];

        for(int i = 0 ; i<n ; i++){
            dp[i] = 1;
            for(int j = 0 ; j < i ; j++){

                if(nums[j]<nums[i]){
                    dp[i] = Math.max(dp[i],dp[j]+1);
                }

            }
            ans = Math.max(ans,dp[i]);
        }
        return ans;

    }
}

最长公共子序列

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

示例 1：

输入：text1 = "abcde", text2 = "ace" 
输出：3  
解释：最长公共子序列是 "ace" ，它的长度为 3 。

示例 2：

输入：text1 = "abc", text2 = "abc"
输出：3
解释：最长公共子序列是 "abc" ，它的长度为 3 。

示例 3：

输入：text1 = "abc", text2 = "def"
输出：0
解释：两个字符串没有公共子序列，返回 0 。

动态规划！

dp[i][j]：text1的前i个和 text2的前j个的最长公共子序列的长度。

当前动作：要不要选i和j的字母算作最长子序列里面？

i和j同时被选只有一种可能：text1【i】=text2【j】，那么dp[i][j]= dp[i-1][j-1]+1

不相等的话，就不可能同时选到最长子串里面，那么dp[i][j]直接= Math.max(dp[i - 1][j], dp[i][j - 1]);

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
        int m = text1.length(), n = text2.length();
        int[][] dp = new int[m + 1][n + 1];
        for (int i = 1; i <= m; i++) {
            char c1 = text1.charAt(i - 1);
            for (int j = 1; j <= n; j++) {
                char c2 = text2.charAt(j - 1);
                if (c1 == c2) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[m][n];
    }
}

划分字母区间

给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。例如，字符串 "ababcc" 能够被分为 ["abab", "cc"]，但类似 ["aba", "bcc"] 或 ["ab", "ab", "cc"] 的划分是非法的。

注意，划分结果需要满足：将所有划分结果按顺序连接，得到的字符串仍然是 s 。

返回一个表示每个字符串片段的长度的列表。

示例 1：

输入：s = "ababcbacadefegdehijhklij"
输出：[9,7,8]
解释：
划分结果为 "ababcbaca"、"defegde"、"hijhklij" 。
每个字母最多出现在一个片段中。
像 "ababcbacadefegde", "hijhklij" 这样的划分是错误的，因为划分的片段数较少。

class Solution {
    public List<Integer> partitionLabels(String S) {
        // 先存每个字母最后一次出现的index
        // 检查第一个字符是否是最后一次出现，如果是，就返回1；
        //          如果不是，tmpIndex跳到该字符最后一次出现的位置，并开始遍历从当前index到tmpIndex的字符：
        //                  如果当前字符是最后一次出现，无事发生，换下一个index++继续判断；
        //                  如果不是最后一次出现，index++，tmpIndex = 该字符最后一次出现的位置
        //          最终，index == tmpIndex以后，跳出循环，ans中加一个tmpIndex - 起始index + 1 ;

        ArrayList<Integer> ans = new ArrayList<>();
        int index = 0;
        int tmpIndex = 0;
        HashMap<Character, Integer> map = new HashMap<>();
        char[] s = S.toCharArray();
        for (int i = 0; i < s.length; i++) {
            map.put(s[i], i);
        }
        while (index < s.length) {
            int start = index;
            
            if(map.get(s[index]) == start){
                ans.add(1);
                index++;
                continue;
            }else{
                tmpIndex = map.get(s[index]);
            }
            int st = index+1;
            while(st<=tmpIndex){
                if(map.get(s[st]) <= tmpIndex){
                    st++;
                    continue;
                }else{
                    tmpIndex = map.get(s[st]);
                    st++;
                }
            }
            ans.add( tmpIndex - start + 1 );
            index = tmpIndex+1;
        }
        

        return ans;



    }
}

每日温度

给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。

示例 :

输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]

思路：

类似于接雨水问题。从右往左看，假设是第i个数，循环看栈尾有没有比他小的，比他小的数在有了nums[i]以后不可能成为前面的数的下一个最高温度了，直接移除removeLast就好。直到跳出这个循环，有两种可能，要么栈被清空了，直接把新的i加入栈中就好；要么栈中还有，就获取栈的尾 - i 作为ans【i】.
再把i放入栈即可。

class Solution {
    public int[] dailyTemperatures(int[] temperatures) {
        Deque<Integer> stack = new ArrayDeque<>();
        int[] res = new int[temperatures.length];
        int n = temperatures.length;
        if (n < 2) return res;
        for (int i = n-1; i >= 0; i--) {
            int tep = temperatures[i];
            while (!stack.isEmpty() && tep >= temperatures[stack.getLast()]) {
                stack.removeLast();
            }
            if (!stack.isEmpty()) res[i] = stack.getLast() - i;
            stack.offerLast(i);
        }
        return res;
    }
}

灵神题单：

一、栈：

1、最后一块石头的重量

有一堆石头，每块石头的重量都是正整数。

每一回合，从中选出两块 最重的 石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

如果 x == y，那么两块石头都会被完全粉碎；
如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。

最后，最多只会剩下一块石头。返回此石头的重量。如果没有石头剩下，就返回 0。

PriorityQueue<Integer> pq = new PriorityQueue<Integer>((a, b) -> b - a);

b - a :从大到小排序； a - b :从小到大排序

class Solution {
    public int lastStoneWeight(int[] stones) {
        PriorityQueue<Integer> pq = new PriorityQueue<Integer>((a, b) -> b - a);
        for (int stone : stones) {
            pq.offer(stone);
        }
        while (pq.size() > 1) {
            int a = pq.poll();
            int b = pq.poll();
            if (a > b) {
                pq.offer(a - b);
            }
        }
        return pq.isEmpty() ? 0 : pq.poll();
    }
}

2、K 次乘运算后的最终数组 I

给你一个整数数组 nums ，一个整数 k 和一个整数 multiplier 。

你需要对 nums 执行 k 次操作，每次操作中：

找到 nums 中的最小值 x ，如果存在多个最小值，选择最前面的一个。
将 x 替换为 x * multiplier 。

请你返回执行完 k 次乘运算之后，最终的 nums 数组。

队列中存的是小的数的序号！！

（a , b ）-> {

if ( nums[a] == nums[b] ){

return a - b ; // 相等的话，就看序号谁小谁在前

}

return nums[a] - nums[b]; // 不相等的话，就看nums【index】谁小谁在前

}

class Solution {
    public int[] getFinalState(int[] nums, int k, int multiplier) {
        PriorityQueue<Integer> pq = new PriorityQueue<>((a,b)->{
            if(nums[a] == nums[b]) {
                return a - b;
            }
            return nums[a] - nums[b];
        });
        for(int i=0; i<nums.length; i++) {
            pq.offer(i);
        }
        while(k>0) {
            int idx = pq.poll();
            nums[idx]*=multiplier;
            pq.offer(idx);
            k--;
        }
        return nums;
    }
}

二、队列

1、单调队列

（1）绝对差不超过限制的最长连续子数组

给你一个整数数组 nums ，和一个表示限制的整数 limit，请你返回最长连续子数组的长度，该子数组中的任意两个元素之间的绝对差必须小于或者等于 limit 。

如果不存在满足条件的子数组，则返回 0 。

输入：nums = [8,2,4,7], limit = 4
输出：2 
解释：所有子数组如下：
[8] 最大绝对差 |8-8| = 0 <= 4.
[8,2] 最大绝对差 |8-2| = 6 > 4. 
[8,2,4] 最大绝对差 |8-2| = 6 > 4.
[8,2,4,7] 最大绝对差 |8-2| = 6 > 4.
[2] 最大绝对差 |2-2| = 0 <= 4.
[2,4] 最大绝对差 |2-4| = 2 <= 4.
[2,4,7] 最大绝对差 |2-7| = 5 > 4.
[4] 最大绝对差 |4-4| = 0 <= 4.
[4,7] 最大绝对差 |4-7| = 3 <= 4.
[7] 最大绝对差 |7-7| = 0 <= 4. 
因此，满足题意的最长子数组的长度为 2 。

核心思路概述:

滑动窗口（双指针）：使用两个指针 left 和 right 表示当前子数组的左右边界。right 指针向右扩展窗口，left 指针在条件不满足时向右收缩窗口。

维护最大值和最小值：使用两个双端队列（queMax 和 queMin）动态跟踪当前窗口内的最大值和最小值：

queMax：一个单调递减队列，队首元素始终是当前窗口的最大值。

queMin：一个单调递增队列，队首元素始终是当前窗口的最小值。

窗口条件：在窗口扩展或收缩过程中，确保 queMax.peekFirst() - queMin.peekFirst() <= limit（即最大值与最小值之差不超过 limit）。如果不满足，则移动 left 指针缩小窗口。

更新结果：在每次窗口有效时（满足条件），计算当前窗口长度 right - left + 1，并更新最大长度 ret。

难理解的部分：

例如queMax队列，这是一个单调递减队列，每次新加一个right指针时，要维持队列的单调性，就要反复判断队伍是不是小于nums[right]。因为right加进来以后，最大值就永远不会是那些比他小的值了，比他小的值直接删了就好。

queMin队列同理！

删完之后，再把nums[right]加到队列里

队列更新完以后就要循环判断left指针形成的滑动窗口是不是满足题目所给的要求，如果不满足，就left++，并且在left++之前，如果left对应的值是max或者min的话，就删掉队列的头。只要跳出这个循环就说明，满足那个题目的条件了，就更新ans值就好。
然后再right更新

public int longestSubarray(int[] nums, int limit) {
    // 初始化两个双端队列：queMax（维护最大值，单调递减），queMin（维护最小值，单调递增）
    Deque<Integer> queMax = new LinkedList<Integer>();
    Deque<Integer> queMin = new LinkedList<Integer>();
    int n = nums.length;
    int left = 0, right = 0; // 滑动窗口的左右指针，初始都指向数组开头
    int ret = 0; // 存储结果（最长子数组长度）

    // 主循环：right 指针遍历整个数组
    while (right < n) {
        // 步骤1：维护 queMax（单调递减队列）
        // 移除队尾所有小于当前元素 nums[right] 的元素，确保队列单调递减
        while (!queMax.isEmpty() && queMax.peekLast() < nums[right]) {
            queMax.pollLast();
        }
        queMax.offerLast(nums[right]); // 将当前元素加入队尾

        // 步骤2：维护 queMin（单调递增队列）
        // 移除队尾所有大于当前元素 nums[right] 的元素，确保队列单调递增
        while (!queMin.isEmpty() && queMin.peekLast() > nums[right]) {
            queMin.pollLast();
        }
        queMin.offerLast(nums[right]); // 将当前元素加入队尾

        // 步骤3：检查当前窗口是否满足条件（最大值 - 最小值 <= limit）
        // 如果不满足，移动 left 指针缩小窗口，直到满足条件
        while (!queMax.isEmpty() && !queMin.isEmpty() && queMax.peekFirst() - queMin.peekFirst() > limit) {
            // 如果左边界元素是当前最小值（queMin 队首），则从 queMin 中移除
            if (nums[left] == queMin.peekFirst()) {
                queMin.pollFirst();
            }
            // 如果左边界元素是当前最大值（queMax 队首），则从 queMax 中移除
            if (nums[left] == queMax.peekFirst()) {
                queMax.pollFirst();
            }
            left++; // 缩小窗口：left 右移
        }

        // 步骤4：更新结果（此时窗口满足条件）
        // 计算当前窗口长度 right - left + 1，并与历史最大值比较
        ret = Math.max(ret, right - left + 1);

        // 步骤5：扩展窗口：right 指针右移
        right++;
    }
    return ret; // 返回最长子数组长度
}