
然后我们再来看一下,再来说一下归一化
比如:在公司有两个人,一个是W2 他能力强,然后领导给他分配的活还少,
然后一个是W1他能力弱,干的慢,但是领导给他分的活多,这个时候他们一起做一个项目的话,那么
就会出现,W2已经干完活了,在那闲着,然后W1还在赶工对吧,这个时候,怎么调整,呢,肯定不能,让他俩掉个个对吧,在机器学习中,公式是固定的没办法分开,这怎么办呢?
可以这样,我们找两个,能力相当的W2,W1,然后给他俩分配,几乎一样的任务,这样就能保证他俩,几乎一块做完工作了.
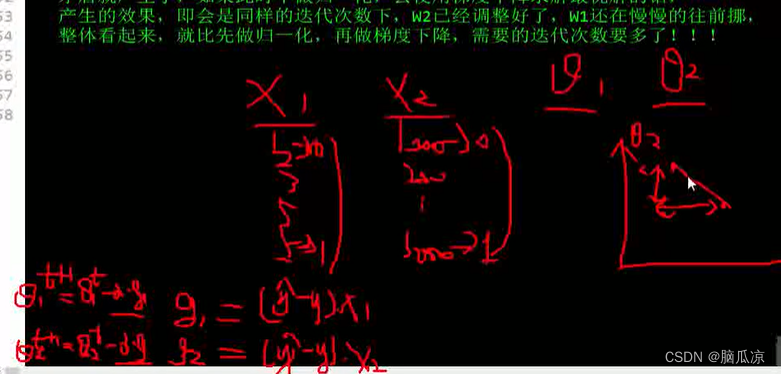
然后比如,我们有两组样本x1 是1 2 3 5 5 ,x2是10000,20000,30000,50000,50000
我们根据y=w0x0这样来说的话,那么x越大,对应的theta就越小对吧,x越小,那么theta就越大,那么
这里如果我们可以让,x1,x2 都差不多大呢?然后可以看到右边画的图,这个时候,如果x1,x2,这两个
样本都可以缩小到同一个范围,并且,不失去原来的意义,那么,最后画出图,就可以是右边这样,那么
他们这个thet








 本文介绍了归一化的重要性,通过调整数据使其处于同一尺度,有助于机器学习中不同特征的公平比较。讨论了sklearn库在分类、回归、聚类和降维等任务中的应用,并特别关注了岭回归防止过拟合的原理,强调简单模型和小权重的优越性。
本文介绍了归一化的重要性,通过调整数据使其处于同一尺度,有助于机器学习中不同特征的公平比较。讨论了sklearn库在分类、回归、聚类和降维等任务中的应用,并特别关注了岭回归防止过拟合的原理,强调简单模型和小权重的优越性。

 订阅专栏 解锁全文
订阅专栏 解锁全文



















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










