机器学习中的归一化问题_梯度下降做归一化的必要性_数据缩放_最大最小值归一化方法---人工智能工作笔记0029

然后我们再来看,为什么说只要是用到了梯度下降法,那么必须要做归一化

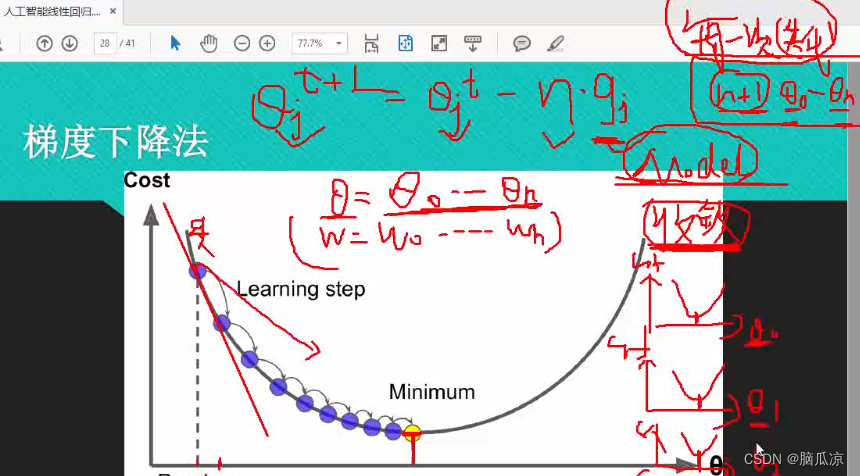
首先我们来看,如果一个人下山,那么我们说,我们每次去求,最优解,也就是利用目标函数,带入theta值,然后求出对应的y值,也就是预测值,然后找到这个点以后,就可以求出斜率对吧,然后斜率,如果

为0的时候,那么就说找到了最优解,但是我们思考一下,现在我们利用随机梯度下降,带入的是

随机的一组样本,所以得到的,斜率,肯定也是一组数据对吧,一组斜率,因为现在我们带入的样本,不是一个数据,是一组数据,所以说,每次,梯度下降,都会得到,比如我们带入了n个,theta数据一次性,那么

我们就会得到n个,斜率值,那么,因为我们用的是随机梯度下降,那么得到的斜率值,肯定,做不到,一次迭代,就让所有的斜率值是最小的,也就是找到最优解,这里,需要通过不停的迭代,让,每一次得到的

一组斜率中的所有的斜率都进行调整,逐步的,让所有的斜率达到,都趋近于0,都达到最优解对吧,相当于,我们带入n个数据的话,m中的第j个样本,拥有n个数据,这就对应了n个正态分布,我们需要让,每个

正态分布的斜率,也就是最优解都算出来,有可能,有些正态分布