论文提出了动态ReLU,能够根据输入动态地调整对应的分段激活函数,与ReLU及其变种对比,仅需额外的少量计算即可带来大幅的性能提升,能无缝嵌入到当前的主流模型中
来源:晓飞的算法工程笔记 公众号
论文: Dynamic ReLU

Introduction
ReLU是深度学习中很重要的里程碑,简单但强大,能够极大地提升神经网络的性能。目前也有很多ReLU的改进版,比如Leaky ReLU和 PReLU,而这些改进版和原版的最终参数都是固定的。所以论文自然而然地想到,如果能够根据输入特征来调整ReLU的参数可能会更好。
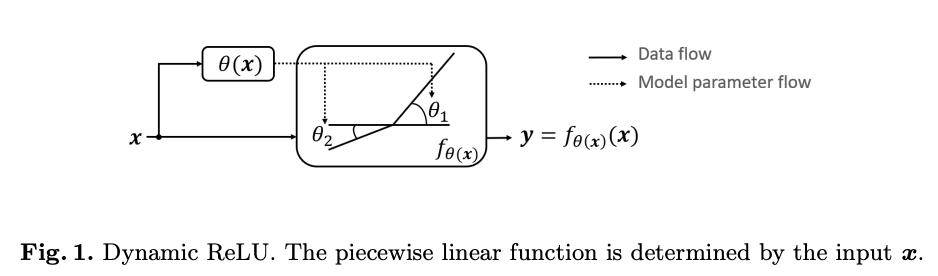
基于上面的想法,论文提出了动态ReLU(DY-ReLU)。如图2所示,DY-ReLU是一个分段函数 f θ ( x ) ( x ) f_{\theta{(x)}}(x) fθ(x)(x),参数由超函数 θ ( x ) \theta{(x)} θ(x)根据输入 x x x得到。超函数 θ ( x ) \theta(x) θ(x)综合输入的各维度上下文来自适应激活函数 f θ ( x ) ( x ) f_{\theta{(x)}}(x) fθ(x)(x),能够在带来少量额外计算的情况下,显著地提高网络的表达能力。另外,论文提供了三种形态的DY-ReLU,在空间位置和维度上有不同的共享机制。不同形态的DY-ReLU适用于不同的任务,论文也通过实验验证,DY-ReLU在关键点识别和图像分类上均有不错的提升。
Definition and Implementation of Dynamic ReLU
Definition
定义原版的ReLU为 y = m a x { x , 0 } y=max\{x, 0\} y=max{x,0}, x x x为输入向量,对于输入的 c c c维特征 x c x_c xc,激活值计算为 y c = m a x { x c , 0 } y_c=max\{x_c, 0\} yc=max{xc,0}。ReLU可统一表示为分段线性函数 y c = m a x k { a c k x c + b c k } y_c=max_k\{a^k_c x_c+b^k_c\} yc=maxk{ackxc+bck},论文基于这个分段函数扩展出动态ReLU,基于所有的输入 x = { x c } x=\{x_c\} x={xc}自适应 a c k a^k_c ack, b c k b^k_c bck:
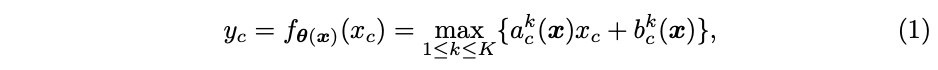
因子 ( a c k , b c k ) (a^k_c, b^k_c) (ack,bck)为超函数 θ ( x ) \theta(x) θ(x)的输出:
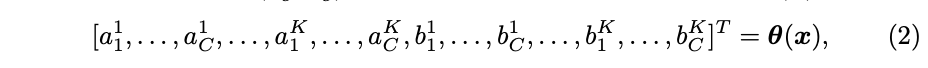
K K K为函数数量, C C C为维度数,激活参数 ( a c k , b c k ) (a^k_c, b^k_c) (ack,bck)不仅与 x c x_c xc相关,也与 x j ≠ c x_{j\ne c} xj=c相关。
Implementation of hyper function θ ( x ) \theta(x) θ(x)
论文采用类似与SE模块的轻量级网络进行超函数的实现,对于大小为 C × H × W C\times H\times W C×H×W的输入 x x x,首先使用全局平均池化进行压缩,然后使用两个全连接层(中间包含ReLU)进行处理,最后接一个归一化层将结果约束在-1和1之间,归一化层使用 2 σ ( x ) − 1 2\sigma(x) - 1 2σ(x)−1, σ \sigma σ为Sigmoid函数。子网共输出 2 K C 2KC 2KC个元素,分别对应 a 1 : C 1 : K a^{1:K}_{1:C} a1:C1:K和 b 1 : C 1 : K b^{1:K}_{1:C} b1:C1:K的残差,最终的输出为初始值和残差之和:
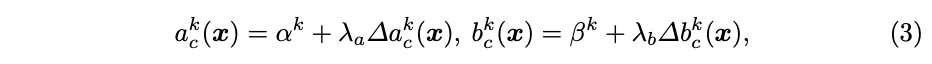
α k \alpha^k αk和 β k \beta^k βk为 a c k a^k_c ack和 b c k b^k_c bck的初始值, λ a \lambda_a λa和 λ b \lambda_b λb是用来控制残差大小的标量。对于 K = 2 K=2 K=2的情况,默认参数为 α 1 = 1 \alpha^1=1 α1=1, α 2 = β 1 = β 2 = 0 \alpha^2=\beta^1=\beta^2=0 α2=β1=β2=0,即为原版ReLU,标量默认为 λ a = 1.0 \lambda_a=1.0 λa=1.0, λ b = 0.5 \lambda_b=0.5 λb=0.5。
Relation to Prior Work
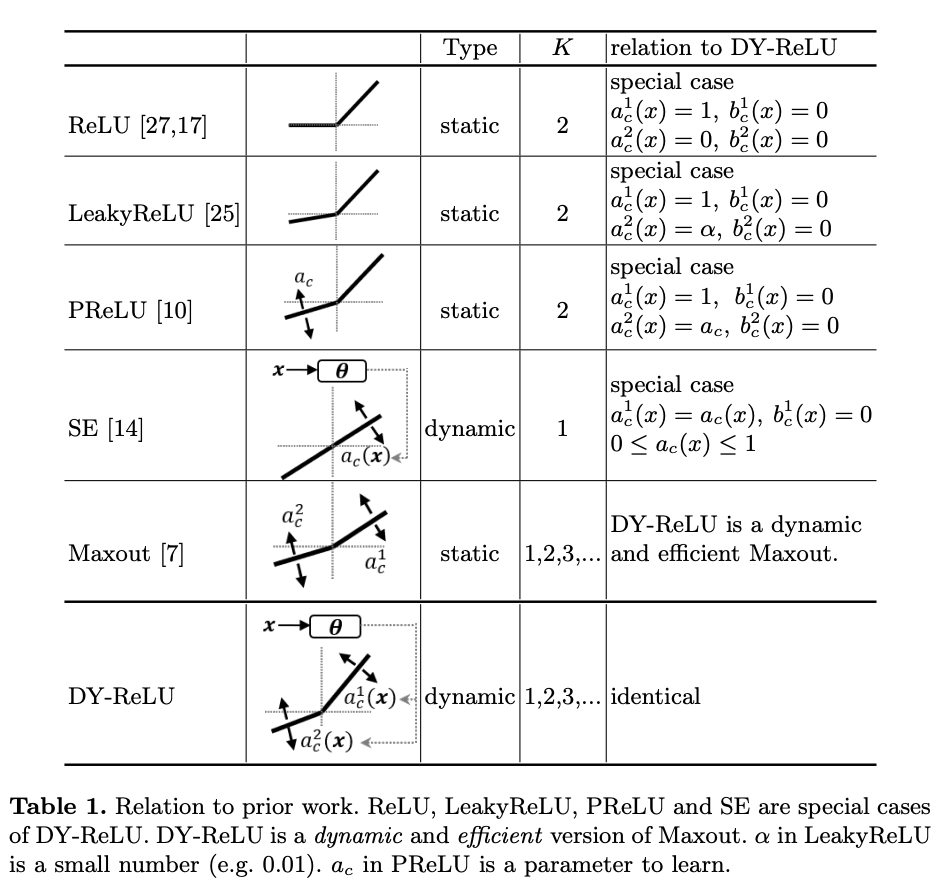
DY-ReLU的可能性很大,表1展示了DY-ReLU与原版ReLU以及其变种的关系。在学习到特定的参数后,DY-ReLU可等价于ReLU、LeakyReLU以及PReLU。而当 K = 1 K=1 K=1,偏置 b c 1 = 0 b^1_c=0 bc1=0时,则等价于SE模块。另外DY-ReLU也可以是一个动态且高效的Maxout算子,相当于将Maxout的 K K K个卷积转换为 K K K个动态的线性变化,然后同样地输出最大值。
Variations of Dynamic ReLU
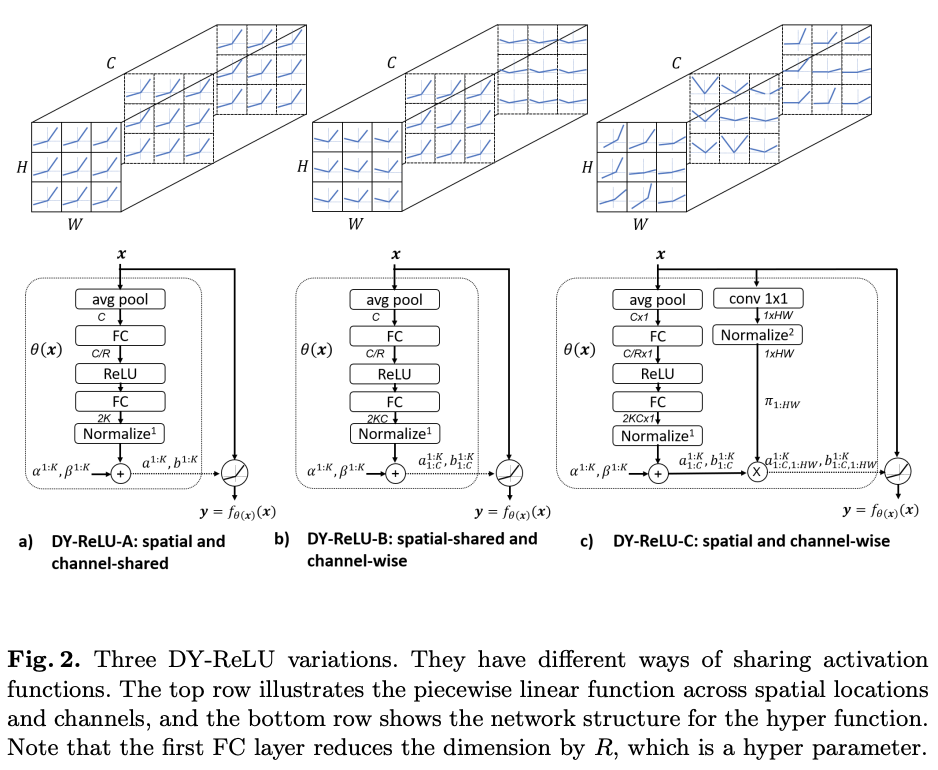
论文提供了三种形态的DY-ReLU,在空间位置和维度上有不同的共享机制:
DY-ReLU-A
空间位置和维度均共享(spatial and channel-shared),计算如图2a所示,仅需输出 2 K 2K 2K个参数,计算最简单,表达能力也最弱。
DY-ReLU-B
仅空间位置共享(spatial-shared and channel-wise),计算如图2b所示,输出 2 K C 2KC 2KC个参数。
DY-ReLU-C
空间位置和维度均不共享(spatial and channel-wise),每个维度的每个元素都有对应的激活函数 m a x k { a c , h , w k x c , h , w + b c , h , w k } max_k\{a^k_{c,h,w} x_{c, h, w} + b^k_{c,h,w} \} maxk{ac,h,wkxc,h,w+bc,h,wk}。虽然表达能力很强,但需要输出的参数( 2 K C H W 2KCHW 2KCHW)太多了,像前面那要直接用全连接层输出会带来过多的额外计算。为此论文进行了改进,计算如图2c所示,将空间位置分解到另一个attention分支,最后将维度参数 [ a 1 : C 1 : K , b 1 : C 1 : K ] [a^{1:K}_{1:C}, b^{1:K}_{1:C}] [a1:C1:K,b1:C1:K]乘以空间位置attention [ π 1 : H W ] [\pi_{1:HW}] [π1:HW]。attention的计算简单地使用 1 × 1 1\times 1 1×1卷积和归一化方法,归一化使用了带约束的softmax函数:
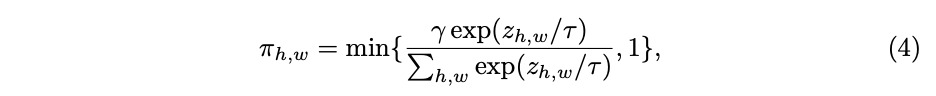
γ \gamma γ用于将attention平均,论文设为 H W 3 \frac{HW}{3} 3HW, τ \tau τ为温度,训练前期设较大的值(10)用于防止attention过于稀疏。
Experimental Results
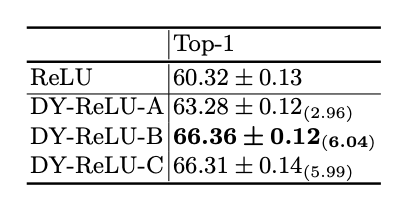
图像分类对比实验。

关键点识别对比实验。
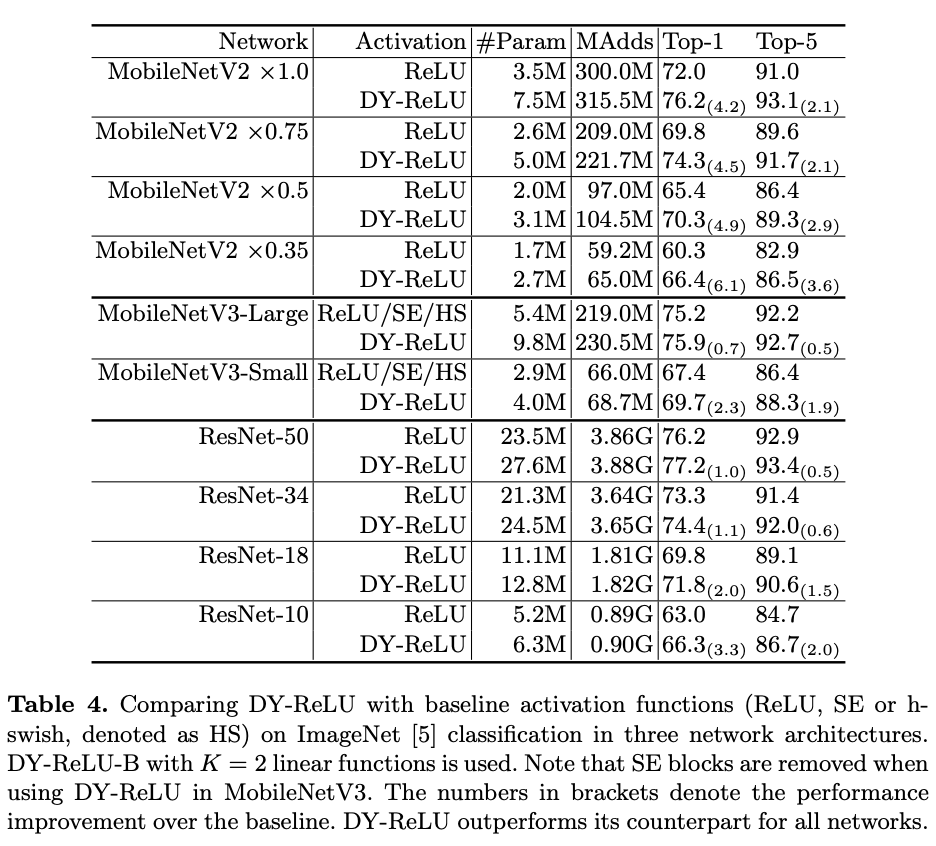
与ReLU在ImageNet上进行多方面对比。
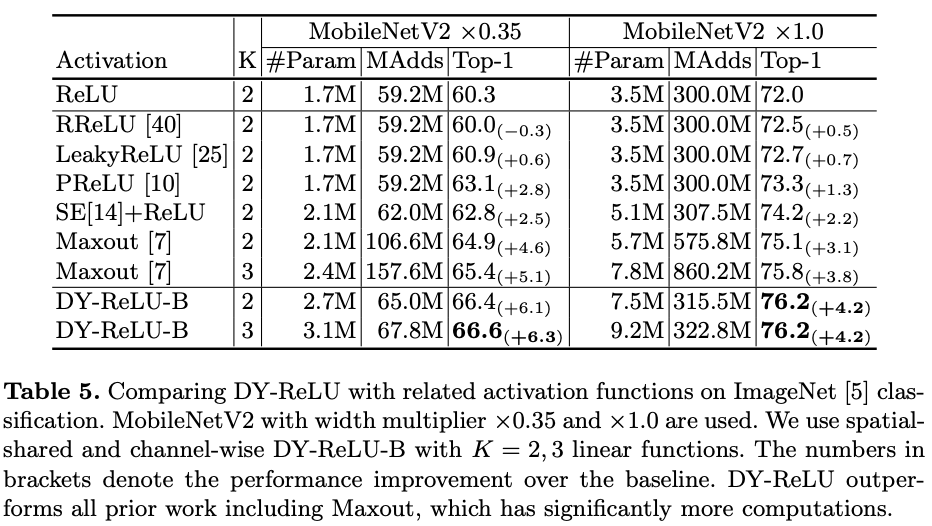
与其它激活函数进行实验对比。
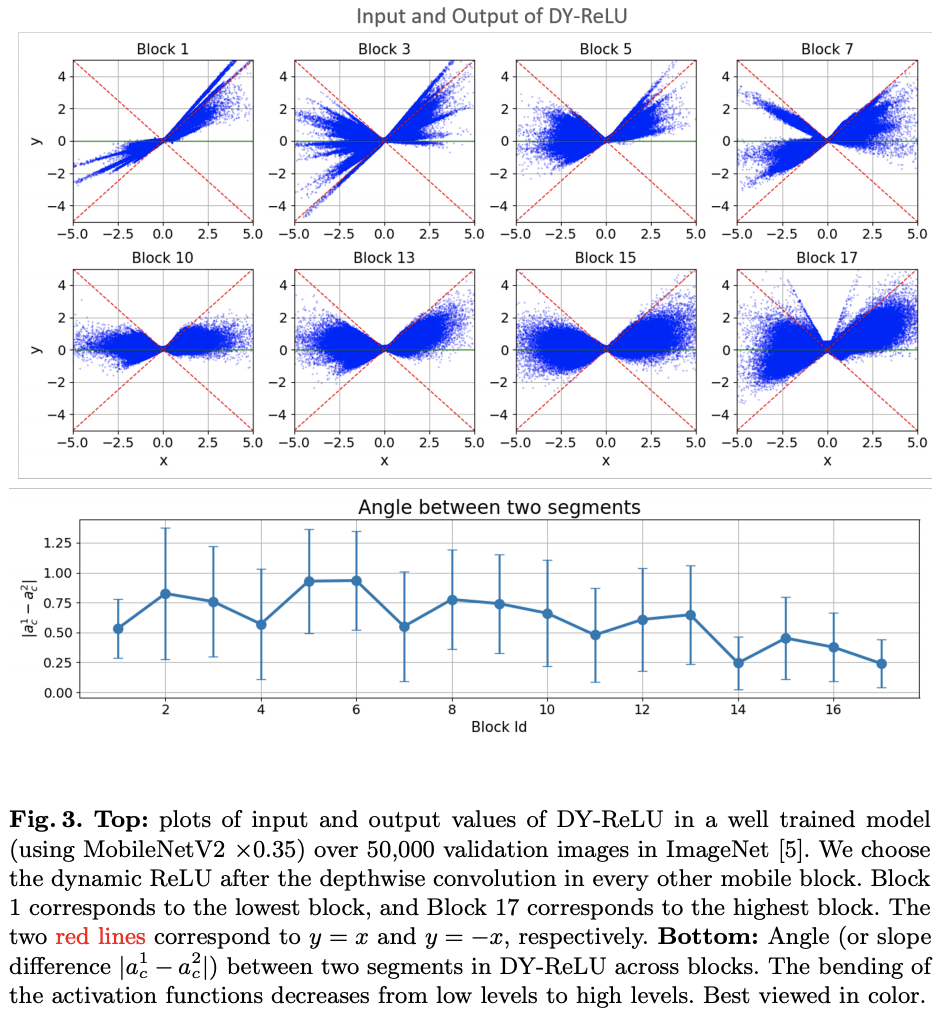
可视化DY-ReLU在不同block的输入输出以及斜率变化,可看出其动态性。
Conclustion
论文提出了动态ReLU,能够根据输入动态地调整对应的分段激活函数,与ReLU及其变种对比,仅需额外的少量计算即可带来巨大的性能提升,能无缝嵌入到当前的主流模型中。前面有提到一篇APReLU,也是做动态ReLU,子网结构十分相似,但DY-ReLU由于 m a x 1 ≤ k ≤ K max_{1\le k \le K} max1≤k≤K的存在,可能性和效果比APReLU更大。
如果本文对你有帮助,麻烦点个赞或在看呗~
更多内容请关注 微信公众号【晓飞的算法工程笔记】























 1840
1840










