离散微分几何基础：流形概念与网格数据结构

一、流形概念的引入

（一）微分几何核心概念——流形

在微分几何的广袤领域中，流形概念占据着核心地位。它如同一个神秘的基石，支撑着我们对各种几何形状和空间的深入理解。就像网格和抽象的单纯复数是我们探索拓扑结构（即事物如何连接）的有力工具一样，它们也为我们揭开流形的神秘面纱提供了关键线索，同时避免我们陷入一些复杂且棘手的问题之中。

（二）k - 形与流形的初步理解

1. **k - 形的概念** - 在踏入流形的奇妙世界之前，我们先来了解一下k - 形这个概念。它是我们理解流形的一个重要前置知识。简单来说，流形是一种具有特定性质的空间概念，而k - 形则是对这种空间概念在不同维度下的一种描述方式。在研究微分几何时，我们常常追求空间具有一些理想的性质，就像在研究曲线时，弧长参数化曲线是一种非常理想的情况。这是因为它能够避免一些奇特且不利于研究的情况发生，比如曲线在某一点处没有明确界定的切线。这种对理想空间性质的追求，促使我们去探索流形以及与之相关的各种概念。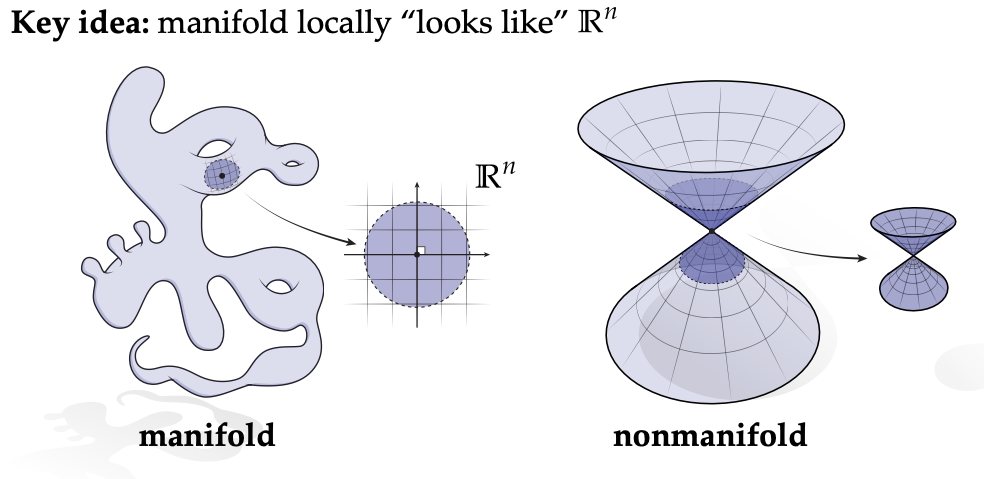

2. 流形的定义尝试
   • 我们试图给流形下一个准确的定义，这需要我们对空间做出一些合理的简化假设。其中一个重要的思路是通过观察形状在每个点邻域的行为来定义流形。如果一个空间在局部呈现出我们熟悉且易于处理的特性，那么它就很有可能是一个流形。
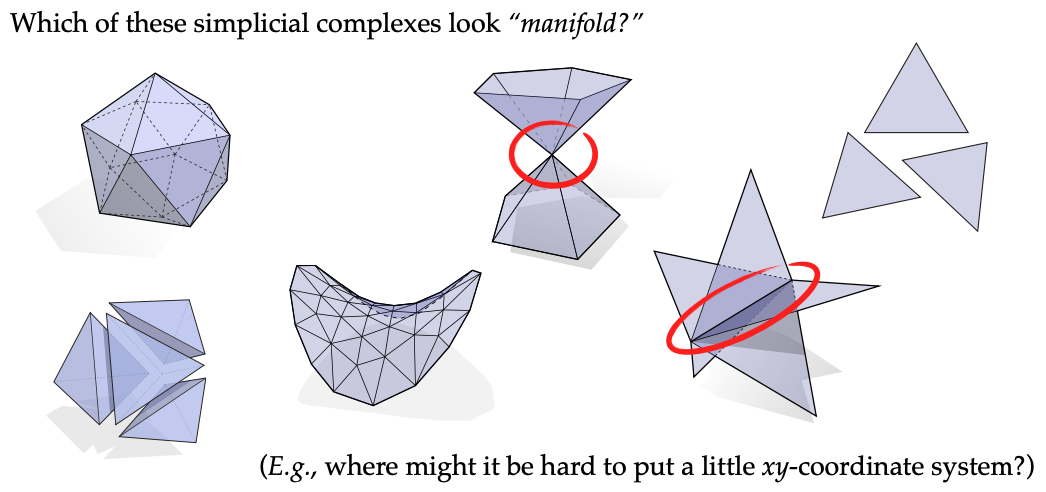
   • 为了更好地理解这一点，我们来看两个具体的形状示例。假设有一个形状，当我们使用放大镜去观察它的每一个微小部分时，我们发现每个点周围都能够相对容易地放置类似于平面的坐标系（也就是我们所说的网格线）。这种在局部能够轻松建立起类似平面结构的特性，使得这个形状在局部具有良好的性质，符合我们对流形的初步期望。然而，对于像沙漏形状这样的特殊图形，当我们聚焦在它中间的那个特殊点时，会发现很难在这个点周围放置合适的坐标系。这个特殊点的存在使得整个沙漏形状无法满足流形在局部性质方面的要求，因此我们判定这个形状是非流形的。

二、流形的判定与示例

（一）基于顶点链接的流形判定

1. **一般判定方法** - 对于一个简化的k - 复数，我们有一个判定它是否为流形的通用方法，即检查每个顶点的链接是否看起来像一个k减去一维球体。这个判定标准是基于流形的本质特性而提出的，它能够帮助我们准确地识别哪些k - 复数具有流形的性质。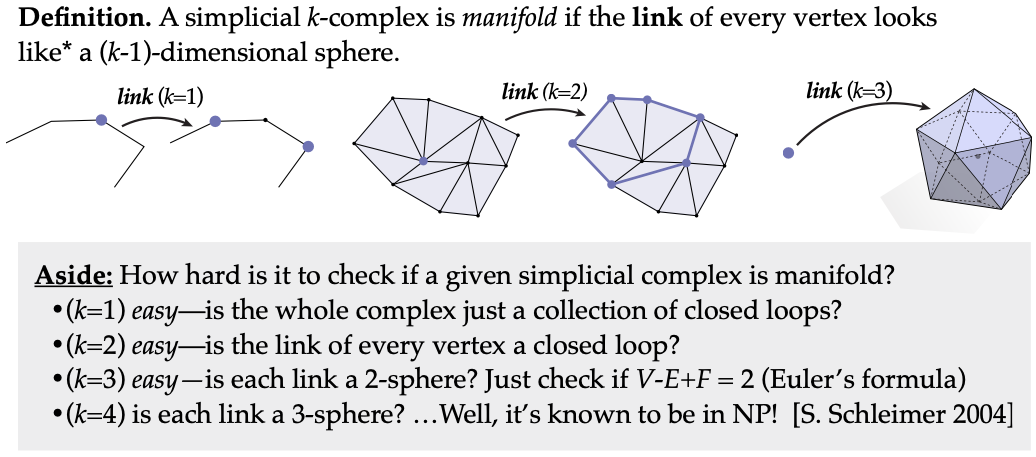

2. 不同维度的示例
   • 让我们通过一些具体的例子来深入理解这个判定方法。首先考虑二维复数的情况，以三角形网格为例。当我们查看其中一个顶点的链接时，如果它形成了一个边循环，这个边循环在拓扑结构上类似于一个圆，那么这个三角形网格在该顶点处满足流形条件。再来看三维复数的情况，比如四面体网格。我们查看其中一个顶点的链接，如果它在拓扑结构上类似于一个简单球体（例如二十面体的结构），那么这个四面体网格在该顶点处也满足流形条件。对于单纯1 - 复数（也就是图的情况），我们查看顶点的链接，会发现它是两个相邻的顶点，这在拓扑结构上类似于一个零维球体（因为零维球体可以看作是实线上所有与原点距离为单位距离的点的集合），所以它也满足流形条件。

（二）不同复杂度下的流形判定

1. **1 - 复数（图）的情况** - 在研究1 - 复数（也就是图）是否为流形时，我们需要关注它的整体结构。当整个图呈现出是一组闭环的形式时，它满足流形的条件。这是因为闭环在拓扑结构上具有一定的规律性和连续性，符合流形的基本特性。然而，如果出现三个边在单个顶点相交的情况，那么这个顶点就不满足流形的定义。因为按照流形的判定标准，这个顶点的链接应该是两个点（类似于零维球体），而现在是三个点，所以这个图在该顶点处不具有流形性质。 2. **简单二复数（三角形网格）的情况** - 对于简单二复数中的三角形网格，判断它是否为流形是相对容易的。我们只需检查每个顶点的链接是否是一个顶点循环（也就是围绕该顶点的顶点形成一个循环）。如果满足这个条件，那么这个三角形网格就是流形的。这是因为这种顶点循环的结构保证了在每个顶点的局部邻域内，网格具有类似于流形的拓扑性质。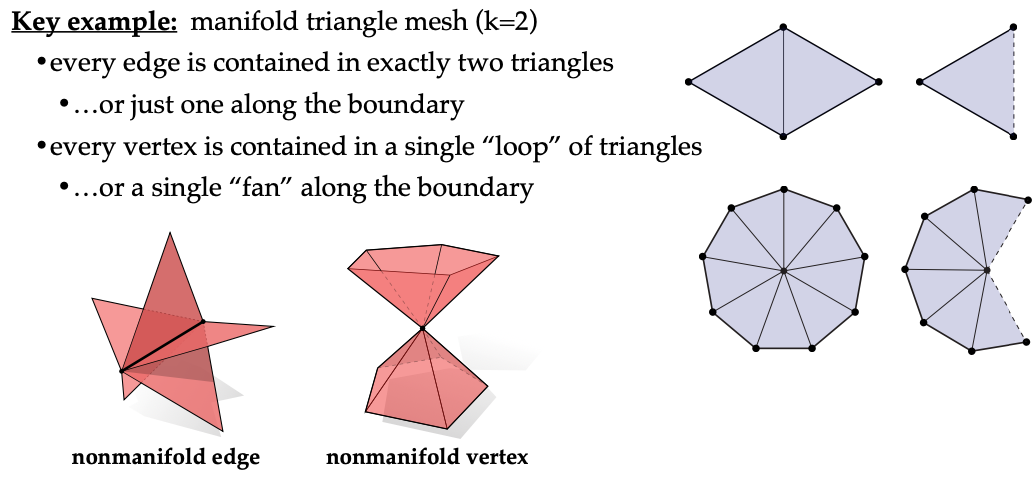

3. 简单3 - 复数（四面体网格）的情况
   • 在简单3 - 复数的四面体网格中，每个顶点的链接是一堆三角形。要判断它是否为流形，我们可以利用欧拉公式。具体来说，我们需要检查所有这些链接的顶点数减去边数加上相位数是否等于2。如果满足这个等式，那么这个四面体网格就是流形的。这个判定方法基于欧拉公式所揭示的拓扑不变性，它能够准确地判断四面体网格在拓扑结构上是否符合流形的要求。

三、流形网格的优势与应用

（一）与二维图像的类比


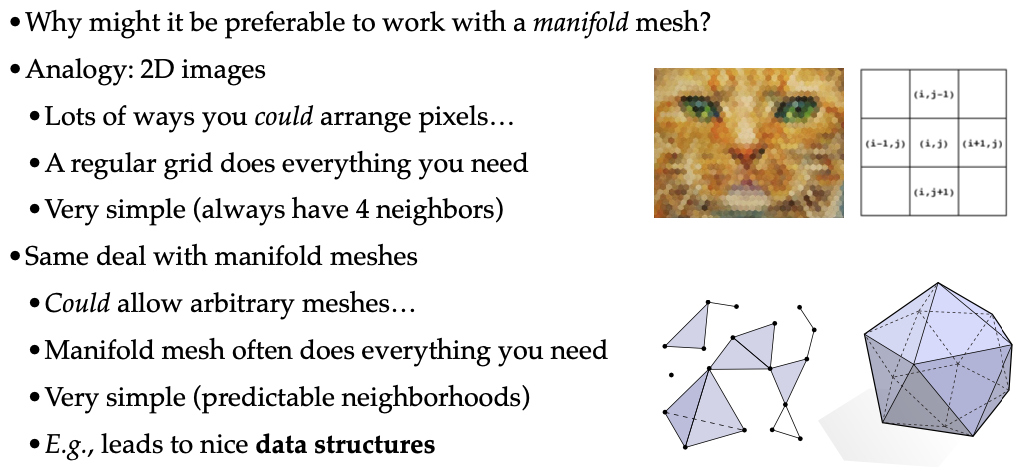1. 规则网格的优势
   • 我们可以通过与二维图像中像素排列的类比来更好地理解流形网格的优势。在二维图像中，像素是构成图像的基本单元，而像素的排列方式多种多样。然而，规则的方形像素网格（也就是我们常见的常规网格）具有独特的优势。它可以满足我们表示各种不同图像的需求，这是因为它具有一种规则且统一的结构。而且，在这种常规网格中，每个像素都有可预测的邻居，通常是四个，分别位于左、右、上、下方向。这种规则性使得我们在处理图像时，其行为具有很高的可预测性，无论是计算像素之间的关系还是进行图像处理算法，都能够更加高效和准确。
2. 流形网格的优势
   • 同样地，流形网格在表示自然几何形状方面也具有显著的优势。它能够捕捉到很多有趣且有用的几何图形信息，这得益于它自身所具有的特殊结构。我们对简单复数的连接方式做出了简化假设，这种假设使得我们能够清晰地了解网格中各个元素之间的连接关系。例如，对于网格中的边，我们知道它左右两边分别连接着的三角形；对于顶点，我们知道它周围的邻居是通过三角形循环来确定的。这种清晰的连接关系使得我们可以设计出非常有效的数据结构来对网格进行编码，从而为后续的几何处理提供了便利。

四、网格数据结构

（一）邻接列表


1. 定义与示例
   • 邻接列表是一种较为基础的拓扑数据结构。它的定义方式相对简单，就是只存储所有顶级维度简化的列表。为了更清楚地理解这一点，我们来看一个具体的例子。假设有一个空心四面体，它是一个简单的II复数，包含四个三角形但没有四面体。我们可以使用邻接列表来对它进行编码，只需要存储这四个三角形的相关信息，比如每个三角形所连接的顶点情况。例如，我们可以记录一个三角形连接顶点0、2以及另外一个（可能存在信息不完整的情况，比如这里提到的“一个”可能是指某个编号，但信息未明确），另一个三角形连接0、3、2和可能存在错误编号的“312”（推测可能是想表达连接3、1、2）等等。
2. 优缺点
   • 邻接列表具有一些明显的优点。首先，它非常简单易懂，对于初学者来说很容易掌握其概念和使用方法。其次，它的存储成本相对较小，因为它只需要存储关于三角形的基本信息，不需要额外存储大量复杂的连接关系。然而，邻接列表也存在一些不足之处。例如，在进行迭代操作时会遇到困难。如果我们想要恰好访问这个网格的每一个边一次，这将是一个比较复杂的过程。我们需要遍历每个三角形的列表来确定与给定顶点相关的边。假设我们有一个非常大的网格，其中包含数十亿个三角形，并且我们给定一个特定的顶点，想要找出接触该顶点的所有边。如果只使用邻接列表，我们就需要遍历整个三角形列表，对于每一个三角形，都要检查它是否包含给定的顶点，如果包含，则需要确定该顶点连接到的其他两个顶点。这样的操作在大规模网格中会导致大量的计算，效率非常低。

（二）入射矩阵


1. 定义与示例
   • 入射矩阵是一种更为复杂和丰富的拓扑数据结构，它能够提供更详细的网格连接信息。对于一个具有n个顶点和m条边的网格，第k个入射矩阵是一个$ (n + 1)×n $矩阵$ e_k $，其中$ e_{kij} $等于1，如果$ j $ - $ k $单纯形包含在$ i $ - $ k + 1 $单纯形中，否则等于0。

以空心四面体为例，我们来详细说明如何构建入射矩阵。首先构建矩阵$ E0 $<fontstyle="color:rgb(28,31,35);">，其中行对应边，列对应顶点。由于空心四面体有四条边和四个顶点，所以</font>$ E0 $<fontstyle="color:rgb(28,31,35);">是一个</font>$ 5×4 $矩阵。对于每条边，如果它连接到某个顶点，就在对应的矩阵条目中放置一个1，否则放置一个0。例如，因为每条边有两个端点，所以每行有两个1。同样，由于每个顶点连接三条边，所以每列有三个1。

再构建矩阵$ E1 $<fontstyle="color:rgb(28,31,35);">，其中行对应三角形，列对应边。同样对于空心四面体，</font>$ E1 $<fontstyle="color:rgb(28,31,35);">是一个</font>$ 4×6 $矩阵。如果某个三角形包含某条边，就在对应的矩阵条目中放置一个1。因为每个三角形有三条边，所以每行有三个1；又因为每条边包含在两个三角形中，所以每列有两个1。

2. 优缺点
   • 入射矩阵的优点在于它能够更丰富地表示网格的连接信息。通过查看矩阵的行列关系，我们可以方便地获取给定顶点的边信息，或者确定包含给定边的三角形信息。例如，要知道与某个顶点相连的边，只需查看$ E0 $<fontstyle="color:rgb(28,31,35);">中对应列的非零元素；要找出包含某条边的三角形，查看</font>$ E1 $中对应列的非零元素即可。
   • 然而，入射矩阵也有其缺点。当网格规模较大时，大部分条目可能为0。这是因为大多数网格单元不在大多数其他网格单元旁边。以一个具有数十亿个面的流形网格为例，对于矩阵$ E1 $，每列通常只有两个1，其余都是0。如果我们显式地存储所有这些条目，将会浪费大量的内存空间。因此，在实际应用中，通常使用稀疏矩阵数据结构来存储入射矩阵。
   • 稀疏矩阵数据结构有多种实现方式。一种是关联数组，它是一个比较自然的概念。通过给定行和列索引，它可以返回对应的值。它可能使用哈希表或树来实现，这种数据结构查找和设置条目非常容易，但进行矩阵运算比较困难，例如矩阵向量乘法。
   • 另一种是链表数组。对于矩阵的每一行，都有一个链表。这个链表存储该行中所有非零条目的信息，包括列索引和对应的值，并且通过指针指向下一个非零条目。这种数据结构在概念上比较简单，但访问时间较慢。如果我们想一直走到行的末尾，需要进行很多操作，并且会有很多不连贯的内存访问。
   • 在实际计算中，大量使用的是类似于压缩列格式的数据结构。这种格式包含三个部分：一个非常紧凑的列表，其中包含所有非零值；一个包含所有相应行索引的列表；以及一个存储每列中累积条目数的列表。这种格式的优点是，如果我们开始对矩阵进行操作，它会非常快。但是，如果我们正在进行矩阵向量乘法，那么添加和删除条目会比较困难，因为这些列表是静态的。在实际应用中，通常先构建一个原始的行列值元组列表，然后再将其转换为一些最终的压缩数据结构。

（三）有符号入射矩阵


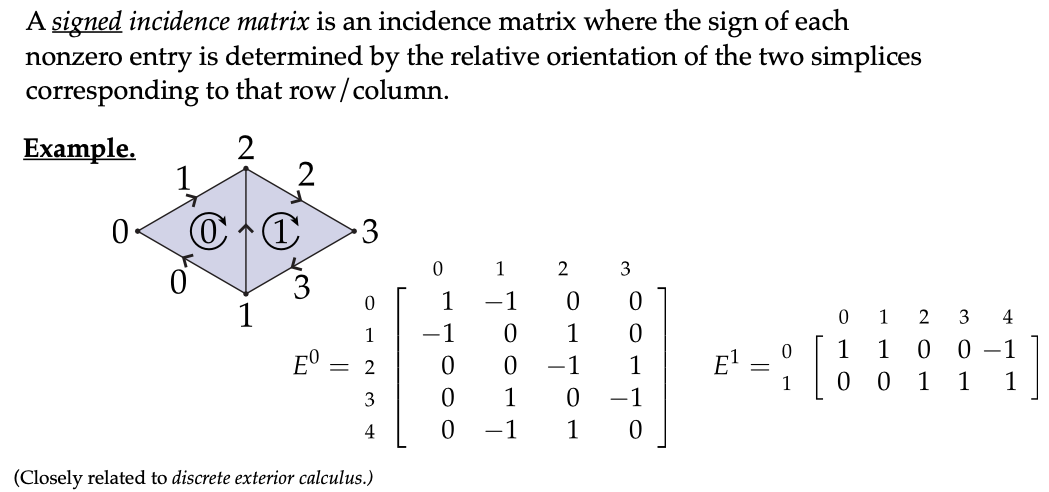1. 定义与示例
   • 有符号入射矩阵是在入射矩阵的基础上进一步扩展得到的。它在条目中不仅有0和1，还有0 + 1或 - 1。每个非零条目的符号由对应行和列的两个单纯性的相对方向决定。
   • 例如，我们考虑一个有方向的三角形网格。假设我们有两个三角形，分别标记为0和1，并且它们具有一致的方向。如果在某个三角形中有一条边从顶点1到顶点2，并且这条边与顶点的方向一致（比如都是顺时针方向），那么在入射矩阵中，对于从顶点1到顶点2的这条边，在对应顶点1的条目中放置 - 1，在对应顶点2的条目中放置 + 1。同样，如果在三角形1中有一条边从2到3，并且这些方向是一致的（都是顺时针方向），那么在矩阵$ E1 $中，查看边2的条目，它是 + 1。而如果有一条边从顶点1到顶点2，位于中间的边（比如是第4条边），且方向不一致（三角形0沿顺时针方向旋转，而这条边是逆时针方向），那么在第0行查看这条边对应的条目，它是 - 1。
2. 与离散外微积分的关系
   • 有符号入射矩阵与离散的外微积分有着直接的关联。尽管它们看起来与普通入射矩阵相似，但它们的含义却截然不同。在离散外微积分中，有符号入射矩阵所包含的符号信息能够更精确地描述几何对象之间的关系，例如在计算一些与方向相关的几何量时，有符号入射矩阵能够提供更准确的信息。这种关系的深入理解对于进一步研究离散微分几何中的各种问题至关重要，它为我们提供了一种更强大的工具来处理和分析几何形状及其性质。

（四）半边网格


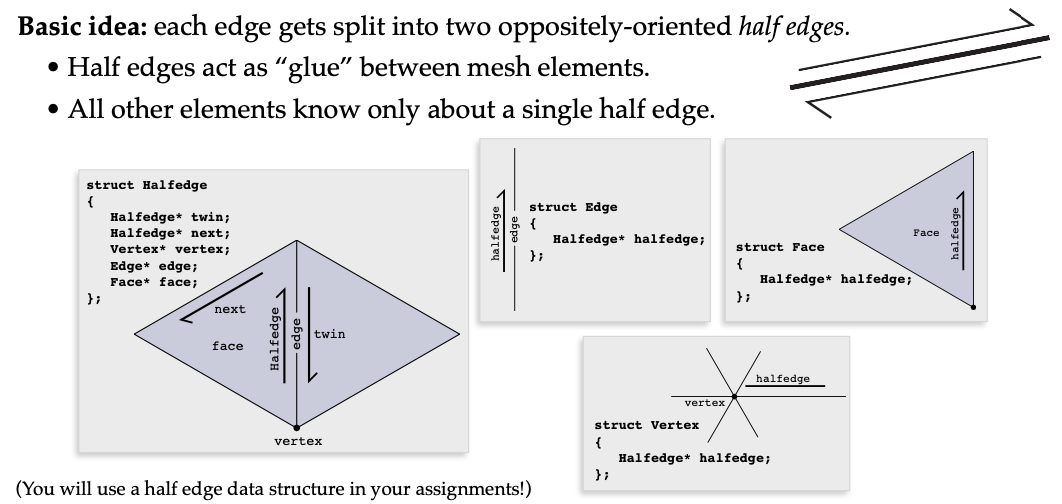1. 基本概念
   • 半边网格是一种在离散微分几何中非常重要的数据结构。它的基本概念是将每条边分成两个相反方向的半边。从直观上看，我们可以把一条边想象成由两个具有特定方向的半边组成，这两个半边在数据结构方面起到了关键的连接作用，它们将所有不同的网格单元紧密地联系在一起。
   • 除了具有方向之外，每个半边还包含了丰富的信息。它知道自己的孪生半边，也就是属于同一条边的另一半边。同时，它也知道下半边是什么，这里的下半边是指围绕某个面循环时接下来的半边。此外，每个半边还清楚自己来自的顶点、所属的边以及所属的面。这种详细的信息使得半边网格在处理网格的连接关系和几何性质计算时具有独特的优势。

2. 半边的代数理解
   • 从代数的角度来看，我们可以对半边网格进行更抽象的理解。假设存在一个集合$ H $<fontstyle="color:rgb(28,31,35);">，这个集合具有偶数个元素，这些元素就代表着半边。同时，存在两个映射：</font>$ \rho $<fontstyle="color:rgb(28,31,35);">和</font>$ \eta $<fontstyle="color:rgb(28,31,35);">。</font>$ \rho $<fontstyle="color:rgb(28,31,35);">是从</font>$ H $<fontstyle="color:rgb(28,31,35);">到</font>$ H $<fontstyle="color:rgb(28,31,35);">的一个映射，它是一种排列，表示下半边的关系；</font>$ \eta <fontstyle="color:rgb(28,31,35);">也是