一、引言
离散微分几何(DDG)作为一个新兴领域,在连接分析描述与计算方面起到了关键作用。它研究光滑几何对象的离散类似物,强调保留系统关键属性的“模拟”观点,区别于传统数值分析注重消除逼近误差的方法。本文将围绕DDG的核心主题,包括平面曲线的离散曲率、离散共形几何、离散微分算子以及离散可积系统等方面展开详细阐述。
二、平面曲线的离散曲率
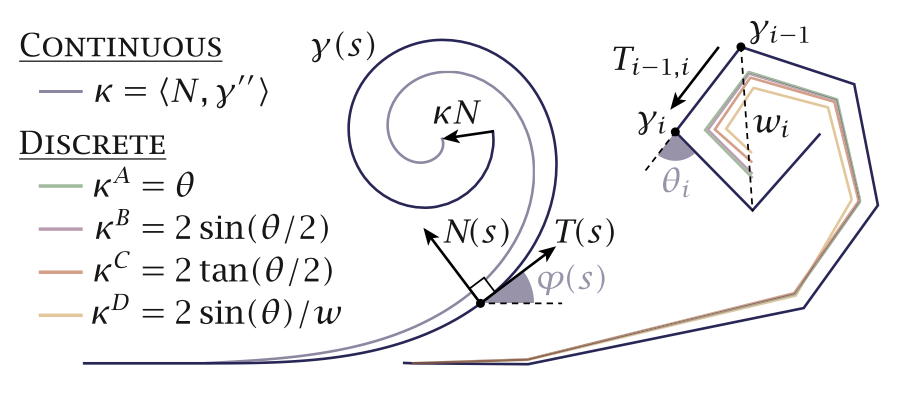(一)光滑曲线曲率定义回顾
对于光滑弧长参数化曲线$ \gamma(s) $,经典的曲率定义方式有多种。一种是通过二阶导数表示,如$ \kappa=\left< N, \frac{d^{2}}{d s^{2}} \gamma\right>=\left< N, \frac{d}{d s} T\right> $,其中$ T $是单位切线,$ N $是单位法线;另一种是通过角度变化与积分关系定义,即$ \int_{a}^{b} \kappa d s=\varphi(b)-\varphi(a) mod 2 \pi $,这里$ \varphi $是从水平线到单位切线$ T $的角度。
(二)离散曲线的曲率定义
对于多边形曲线,由于在顶点不可二次求导且法线无定义,因此存在多种离散曲率定义方式:
基于角度变化的定义( $ \kappa_{i}^{A} $)
定义:对于多边形曲线的顶点$ i <fontstyle="color:rgb(28,31,35);">,设</font><font style="color:rgb(28, 31, 35);">,设</font> < f o n t s t y l e = " co l or : r g b ( 28 , 31 , 35 ) ; " > ,设 < / f o n t > <fontstyle="color:rgb(28,31,35);">和</font><font style="color:rgb(28, 31, 35);">和</font> < f o n t s t y l e = " co l or : r g b ( 28 , 31 , 35 ) ; " > 和 < / f o n t > <fontstyle="color:rgb(28,31,35);">是与顶点</font><font style="color:rgb(28, 31, 35);">是与顶点</font> < f o n t s t y l e = " co l or : r g b ( 28 , 31 , 35 ) ; " > 是与顶点 < / f o n t > <fontstyle="color:rgb(28,31,35);">相邻的两条边的方向角,则</font><font style="color:rgb(28, 31, 35);">相邻的两条边的方向角,则</font> < f o n t s t y l e = " co l or : r g b ( 28 , 31 , 35 ) ; " > 相邻的两条边的方向角,则 < / f o n t > <fontstyle="color:rgb(28,31,35);">,且</font><font style="color:rgb(28, 31, 35);">,且</font> < f o n t s t y l e = " co l or : r g b ( 28 , 31 , 35 ) ; " > ,且 < / f o n t > 思路:通过计算相邻边方向角的差值来确定顶点处的离散曲率。 基于长度变化和单位角平分线的定义( $ \kappa_{i}^{B} $)
定义:设$ L:=\sum_{i = 1}^{n - 1}|\gamma_{i + 1}-\gamma_{i}| <fontstyle="color:rgb(28,31,35);">为多边形曲线的总长度,对总长度关于顶点位置求偏导,在顶点</font><font style="color:rgb(28, 31, 35);">为多边形曲线的总长度,对总长度关于顶点位置求偏导,在顶点</font> < f o n t s t y l e = " co l or : r g b ( 28 , 31 , 35 ) ; " > 为多边形曲线的总长度,对总长度关于顶点位置求偏导,在顶点 < / f o n t > <fontstyle="color:rgb(28,31,35);">处得到</font><font style="color:rgb(28, 31, 35);">处得到</font> < f o n t s t y l e = " co l or : r g b ( 28 , 31 , 35 ) ; " > 处得到 < / f o n t > <fontstyle="color:rgb(28,31,35);">,如果</font><font style="color:rgb(28, 31, 35);">,如果</font> < f o n t s t y l e = " co l or : r g b ( 28 , 31 , 35 ) ; " > ,如果 < / f o n t > <fontstyle="color:rgb(28,31,35);">是顶点处的单位角平分线,则</font><font style="color:rgb(28, 31, 35);">是顶点处的单位角平分线,则</font> < f o n t s t y l e = " co l or : r g b ( 28 , 31 , 35 ) ; " > 是顶点处的单位角平分线,则 < / f o n t > 思路:考虑多边形曲线总长度关于顶点位置的偏导数,并结合顶点处的单位角平分线来计算离散曲率。 基于曲线长度变化和不同边偏移方式的定义( $ \kappa_{i}^{C} $)
定义:将多边形曲线分成单个边,分别沿各自的法向方向平移$ \varepsilon <fontstyle="color:rgb(28,31,35);">,然后通过不同方式闭合边之间的间隙。用直线闭合时,</font><font style="color:rgb(28, 31, 35);">,然后通过不同方式闭合边之间的间隙。用直线闭合时,</font> < f o n t s t y l e = " co l or : r g b ( 28 , 31 , 35 ) ; " > ,然后通过不同方式闭合边之间的间隙。用直线闭合时, < / f o n t > {B}=length(\gamma)-\varepsilon \sum {i = 2}^{n - 1} 2 sin \left(\theta_{i} / 2\right) <fontstyle="color:rgb(28,31,35);">,对应的离散曲率为</font><font style="color:rgb(28, 31, 35);">,对应的离散曲率为</font> < f o n t s t y l e = " co l or : r g b ( 28 , 31 , 35 ) ; " > ,对应的离散曲率为 < / f o n t > <fontstyle="color:rgb(28,31,35);">;用延长边直到相交闭合时,</font><font style="color:rgb(28, 31, 35);">;用延长边直到相交闭合时,</font> < f o n t s t y l e = " co l or : r g b ( 28 , 31 , 35 ) ; " > ;用延长边直到相交闭合时, < / f o n t > {C}=length(\gamma)-\varepsilon \sum {i = 2}^{n - 1} 2 tan \left(\theta_{i} / 2\right) <fontstyle="color:rgb(28,31,35);">,对应的离散曲率为</font><font style="color:rgb(28, 31, 35);">,对应的离散曲率为</font> < f o n t s t y l e = " co l or : r g b ( 28 , 31 , 35 ) ; " > ,对应的离散曲率为 < / f o n t > 思路:通过将多边形曲线的边在法向方向上进行小位移,然后根据不同的闭合边间隙方式所得到的新曲线长度变化来定义离散曲率。 基于外接圆半径的定义( $ \kappa_{i}^{D} $)
定义:对于多边形曲线的顶点$ i <fontstyle="color:rgb(28,31,35);">,设</font><font style="color:rgb(28, 31, 35);">,设</font> < f o n t s t y l e = " co l or : r g b ( 28 , 31 , 35 ) ; " > ,设 < / f o n t > <fontstyle="color:rgb(28,31,35);">,则</font><font style="color:rgb(28, 31, 35);">,则</font> < f o n t s t y l e = " co l or : r g b ( 28 , 31 , 35 ) ; " > ,则 < / f o n t > <fontstyle="color:rgb(28,31,35);">,其中</font><font style="color:rgb(28, 31, 35);">,其中</font> < f o n t s t y l e = " co l or : r g b ( 28 , 31 , 35 ) ; " > ,其中 < / f o n t > 思路:根据多边形顶点与其相邻两个顶点所构成三角形的外接圆半径来计算离散曲率。 (三)不同定义的比较与选择
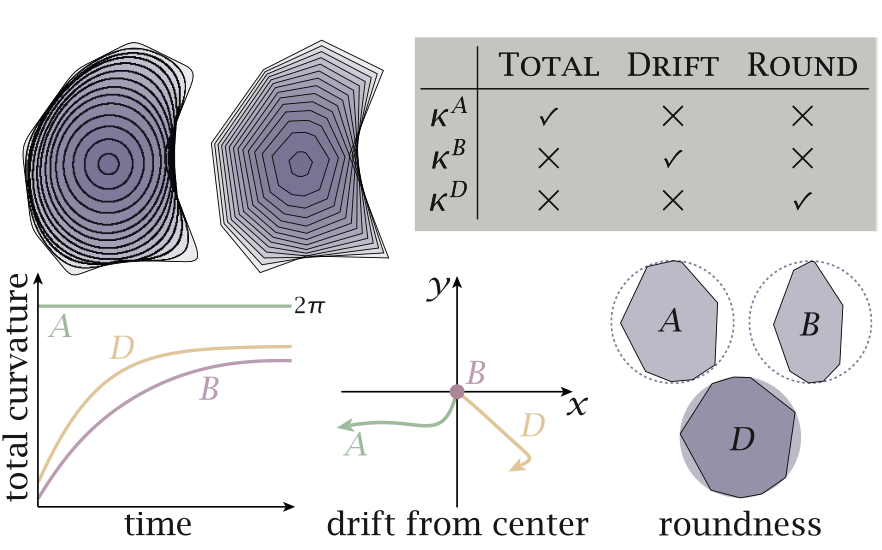
不同的离散曲率定义在收敛性和性质保留上各有特点。例如,对于曲线缩短流:
$ \kappa^{A} $保留总曲率,这是因为它基于角度变化的定义与光滑曲线曲率通过角度积分定义有一定的关联。 $ \kappa^{B} $保留质心,从其定义基于曲线长度关于顶点位置的偏导可以看出它对质心相关性质的保留。 $ \kappa^{D} $使圆形多边形为极限点,这与它基于外接圆半径的定义方式相关。 三、离散共形几何
(一)共形映射的概念
共形映射大致是保角映射。在光滑情形下,任何表面可共形映射到常曲率空间,且共形映射可高效计算,在数字几何处理算法中有广泛应用。
(二)离散共形映射的定义
1. **基于角度保留的定义局限**
- 如果要求离散映射保留所有角度,只能得到可展的离散曲面。例如,对于一个 simplicial map将一个 triangulated disk映射到平面上的 triangulation,如果保留内角,只能是相似变换,对于相邻三角形由于共享边,所有三角形的缩放因子必须相同,这导致只有可展的离散曲面满足条件,与光滑情形下任何圆盘可共形映射形成对比。
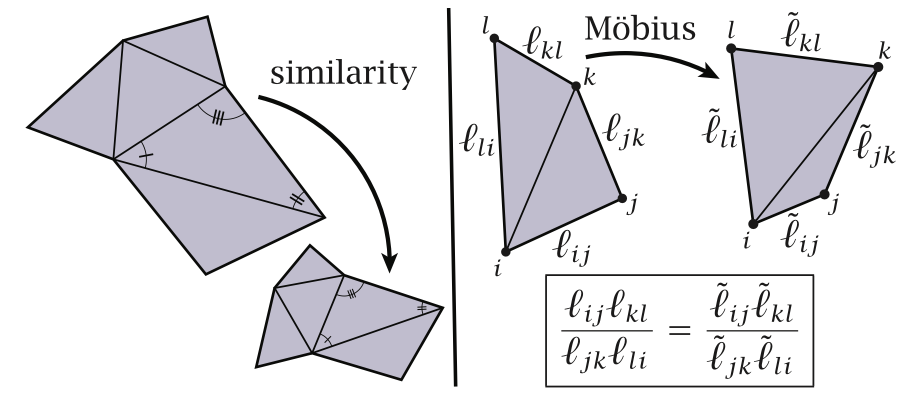
2. **圆填充定义**
- 可以将离散圆盘的每个顶点与平面上的圆相关联,根据Koebe定理,可以安排这些圆使得属于共享边的两个圆相切且所有边界圆与一个公共圆相切。对于规则三角晶格逼近一个区域,这种圆填充可以近似光滑的共形映射,并且保留了共形映射的一些基本结构性质,如与Möbius变换的关系。
3. **基于度量均匀缩放的定义**
- 从共形映射下度量均匀缩放的角度定义离散共形等价。在 simplicial setting中,用 piecewise Euclidean metric替换Riemannian metric,如果两个这样的 metrics满足一定关系($ \tilde{\ell}_{ij}=e^{(u_{i}+u_{j})/2} \ell_{ij} $对于离散 scale factors $ u: V \to \mathbb{R} $),则称它们是离散共形等价的。这种定义方式也与长度 cross ratios的保留相关,并且对于嵌入在$ R^{n} $中的网格,这些 ratios在Möbius变换下是不变的,类似于光滑理论。
(三)不同定义的比较与选择
不同的离散共形映射定义在计算上有不同权衡,且对于不规则三角剖分需要不同的理论。例如,基于角度保留的定义计算简单但过于严格,只适用于可展曲面;圆填充定义在保留结构性质上有优势但对于不规则三角剖分需要进一步理论完善;基于度量均匀缩放的定义在理论上更完整但计算可能相对复杂。
四、离散微分算子
(一)拉普拉斯 - 贝尔特拉米算子回顾
在光滑情形下,拉普拉斯 - 贝尔特拉米算子(简称拉普拉斯算子)作用于微分k - 形式,与热扩散、波传播等物理现象及拓扑信息相关。例如,在封闭的Riemannian流形上,谐波k - 形式(在拉普拉斯算子核中的那些)的维度等于k - 上同调的维度(一个纯粹的拓扑量),拉普拉斯算子的谱(特征值列表)也揭示了流形的几何信息。
(二)离散拉普拉斯算子的定义
在可定向有限单纯流形(如多面体表面)中,通过单纯边界算子$ \partial_{k}: C_{k} \to C_{k - 1} $和对偶算子$ \delta_{k}: C^{k} \to C^{k + 1} $定义。配备正定内积$ (\cdot, \cdot)_{k} $后,可定义拉普拉斯算子$ \Delta_{k}:=\delta_{k}^{*} \delta_{k}+\delta_{k - 1} \delta_{k - 1}^{*} $,并得到离散霍奇分解$ C^{k}=ker\left(\Delta_{k}\right) \oplus im\left(\delta_{k - 1}\right) \oplus im\left(\delta_{k}^{*}\right) $。
(三)内积的选择
不同内积选择有不同结果:
平凡内积
导致纯组合图拉普拉斯算子,不收敛到光滑情形。因为平凡内积没有考虑到几何结构的更多信息,只是基于图的组合结构定义。 线性插值(惠特尼元素)
对于$ n = 2 $得到cotan拉普拉斯算子。线性插值考虑了更多的几何信息,通过对-cochains over - dimensional simplices进行插值,使得定义的拉普拉斯算子在某些性质上更接近光滑情形。 五、离散可积系统
(一)参数化曲面理论回顾
以用鱼网丝袜包裹表面的问题为例,它对应一种特殊的平铺,其在无穷小处是弱切比雪夫网。对于特殊的K - 表面(常高斯曲率$ K = -1 $),可得到渐近参数化和正弦 - 戈登方程。
(二)离散版本
1. **离散正弦 - 戈登方程**
- Hirota得到离散版本的正弦 - 戈登方程。
2. **离散K - 表面的定义与方程恢复**
- Bobenko和Pinkall给出离散K - 表面的几何定义并恢复该方程。离散K - 表面被定义为离散(弱)切比雪夫网且所有四个与任何顶点相连的边位于一个公共平面。
3. **离散高斯曲率相关定义**
- 最近也有离散高斯曲率的相关定义使得离散K - 表面具有常负高斯曲率。对于离散K - 表面(所有边长度相等的情况即菱形情况),一个顶点的四个相邻顶点必须位于一个公共圆上,通过考虑四边形的对角线子集可得到另一种四边形网格,其所有四边形都有外接圆,即所谓的cK - 网。在离散设置中,圆形四边形的规则网络起到了曲率线参数化表面的作用,这一变换模拟了光滑设置中渐近线的角平分线是主曲率线的情况。更广泛地说,具有特殊关联关系的四边形网络理论与建筑几何领域的物理制造考虑密切相关。例如,若每个顶点周围的四个四边形都与一个公共圆锥相切,则该四边形网络是圆锥形的,这样的表面允许具有恒定宽度的面偏移,使其对(例如)玻璃面板结构的建造具有吸引力。
六、结论
离散微分几何通过对平面曲线离散曲率、离散共形几何、离散微分算子和离散可积系统等方面的研究,为几何对象的离散化处理提供了丰富的理论和方法。这些研究成果在计算解剖学/生物学、计算力学、工业设计、计算建筑学和数字几何处理等众多领域都具有潜在的应用价值。然而,不同的离散定义和方法都有其自身的优势和局限性,在实际应用中需要根据具体问题的需求和特点进行合理选择和运用。未来,离散微分几何领域还有待进一步深入研究和发展,例如对离散定义的进一步优化和完善,以及探索更多的应用场景和实际应用案例等。






















 2051
2051

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








