初学SLAM二之BA当中的数学知识点

最新推荐文章于 2025-07-04 11:14:01 发布

神笔马良2018

最新推荐文章于 2025-07-04 11:14:01 发布

阅读量3.3k

点赞数 1

CC 4.0 BY-SA版权

分类专栏： C++/OpenCV 图像处理 SLAM BA优化

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.youkuaiyun.com/liangqichan/article/details/83098144

本文介绍了SLAM中的Bundle Adjustment（BA）的基本概念，即通过最小化重投影误差来确定相机位姿和特征点的世界坐标。文章详细讲解了最速下降法、牛顿法、高斯-牛顿法和Levenberg-Marquardt（L-M）法等四种数值优化方法的数学原理，并提供了例题帮助理解这些方法的运用。BA的核心在于非线性最小二乘问题的解决，这四种方法分别从一阶和二阶导数的角度出发，寻求优化解。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

SLAM的BA，本人的理解是通过我们计算的到的各个像素特征点在世界坐标系当中的三维坐标，通过相机模型，重投影到相片中的像素坐标，最小化多个位置点和多个特征点重投影误差。

最终建立的方程为：

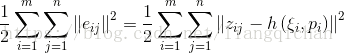
其中左边表示为第i个相机，第j个特征点的重投影误差之和，右边zij表示第i个相机第J个特征点在原始图像中的实际像素位置， $\xi _{i}$ 表示第i'个相机的位姿，pi表示第i个特征点的世界坐标系位置。

BA的任务就是获取使得上式右边值最小化时， $\xi _{i}$ 的取值。因此，需要用到非线性最小二乘的知识。下面就是本篇博客的重点，介绍BA当中最常用的四种数值优化方法，最速下降发，牛顿法，G-N法和L-M法。包括数学原理，各个方法的例题。

1最速下降法

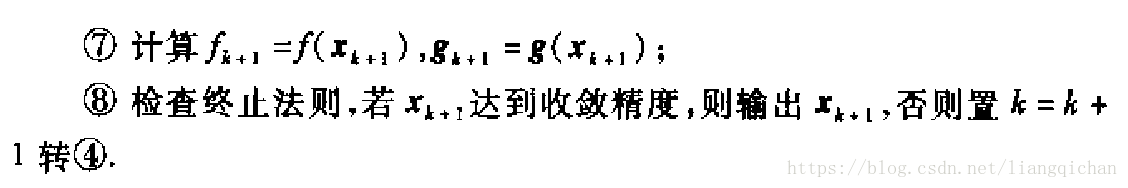
其中梯度g(x)为f(x)关于所有变量x的偏导数矩阵，也称雅可比矩阵 (Jacobian矩阵)。因此最速下降法的增量p=-g(x)

觉得步骤难以理解，下面辅助一个简单的例

最低0.47元/天解锁文章

200万优质内容无限畅学

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。