RNN、LSTM、GRU

• 近年来循环神经网络在自然语言处理，语音技术，甚至图像方面都有不错的应用。本文主要介绍基础的RNN，RNN所面对的问题，以及RNN的改进版本：LSTM和GRU

RNN(Recurrent Neural Network)

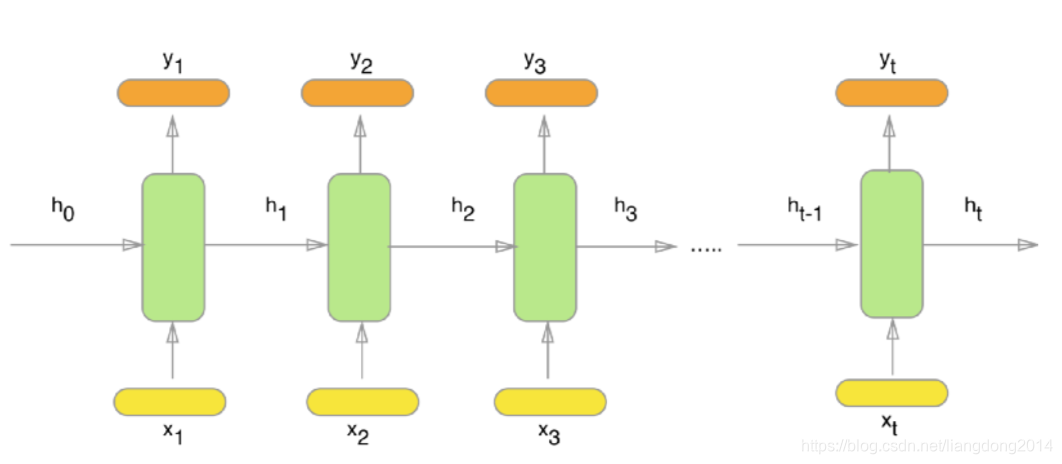
• 我们先放一张RNN的结构图，一般的RNN也遵循这个过程。输入是x1～xt，绿色的方框表示处理单元，$h_i$表示的是隐藏单元，$y_i$表示的是输出。对于不同的输入$x_i,h_i$，RNN的cell(一个绿色框)都是彼此之间共享参数的。
• 一般来说RNN的计算过程分成下面的步骤：
  1. 构造数据，形成{x1,x2, …, xt}的sample
  2. 将$x_i$输入给第$i$个单元,进行计算，分别得到$y_i,h_i$
  3. 重复上述第二步，得到$y_0,...,y_n$,计算loss
  4. 反向传播，更新绿色框中的参数
  5. 重复1～4，直到网络收敛
• 那么绿色框中到底是什么呢？他是怎么做到记录了上一个输入的信息呢？
• Standard RNN Cell
  • 标准的RNN cell如下图所示，它里面其实就是封装了一层神经网络和一个非线性处理单元。
    
  • 公式化如下：
    • $h_i=f(W^{hh}{h}_{i-1}+W^{hx}{x}_i)$，其中$f$代表非线性激活函数，例如sigmoid(下面会以其举例说明RNN缺点)。
    • $y_i=softmax(W^y{h}_i)$,其中y是输出。
  • 它是怎么记下过去的信息的呢？是通过隐藏状态$h_i$记下的。我的理解是是因为我们通过BP优化的是它，所以赋予了$h_i$这么个意义，至于怎么证明$h_i$就是过去的信息，还有待探索。
  • 缺点：如果输入sample里面时刻太长的话，可能会导致梯度消失，从而忘记很早时刻的信息。
    • 为了从数学的角度说明上面那一点，我们就先从BP推导起来。
    • 假设$E$表示损失函数,令$s=W^{y}h,y_i=softmax(s_i)$
    • $\frac{\partial E}{\partial W^{hh}}={\sum }_{i=1}^k\frac{\partial E}{\partial y}\ast \frac{\partial y}{\partial s}\ast \frac{\partial s}{\partial h_i}\ast \frac{\partial h_i}{\partial W^{hh}}$
    • 其中$i$表示的第i时刻，$k$表示的是一共有$k$个时刻。
    • 我们知道，在计算第$i$时刻的梯度的时候，它与$i+1->k$时刻都有关系。并且这种关系表现在梯度上是惩罚的关系。所以我们可以得到下面的等式
    • $\frac{\partial s}{\partial h_i}={\Pi }_{j=i+1}^k\frac{\partial h_j}{\partial h_{j-1}}={\Pi }_{j=i+1}^k{f}^{\prime }(h_j)$
    • 正如我们上面所说,f(x) = sigmoid，其导数范围在0～1之间，如果我们有多个小数相乘的话，就会导致梯度为0，从而导致梯度消失。
    • 注意，我们这里的梯度消失只是针对比较靠前的输入来说，说明其输入没有起到合适的作用(梯度为0)。但是对于靠后的输入来说梯度还是存在的。因为观察上面的公式我们就可以得到靠后的梯度j~k连乘的次数少。
    • 至此，我们说了$W_{hh}$在long sequence的传播过程中是如何产生梯度消失问题的。注意$W_y$应该是不会有这个问题的。因为它一般只会更新一次(如果我们只用$y_k$去计算loss的话)。同理$W_{hx}$也是会存在这个问题的。
  • 如何解决梯度消失问题呢？sigmoid既然梯度为0，那么relu呢？relu可能会导致梯度爆炸问题。因为relu(x) = x，他没有限制x的取值范围。此外relu的导数是一个常数，他不会随着x的变化而变化。sigmoid通过限制输出的大小，从而限制的整个网络的幅度。那么如何结合relu的问题的？可以使用Batch Normalization, 参考这篇博文。
  • 请看下面LSTM和GRU的解决方案。

LSTM (Long Short-term Memory)

• 正如上面说的普通的RNN会导致梯度消失的问题，那么LSTM是如何解决的呢？
• 我们先放一张LSTM的cell，如下图所示
  
  • LSTM Cell里面有如下几个重要的概念(四门一态)：
    • forget gate
    • input gate
    • update gate
    • output gate
    • Cell state
  • forget gate：生成一个mask，决定cell state里面哪些信息应该被遗忘，哪些信息应该被保留。forget可以看成是对cell stage的forget。
    • 其是由$h_i,x_i,sigmoid$组成，如下图所示
      
    • 其中f_t就代表forget gate的输出，它表示了我们要选择性的遗忘cell state里面的某些值(对应位置的f_t为0或者是低响应区域)。
    • 从公式的角度来看：$f_t=W_{fh}{h}_{i-1}+W_{fx}{x}_i$
  • input gate：决定新的输入中哪些信息应该被加入的cell state中。所以input可以看成是对cell state的输出。
    • 其是由$h_{i-1},x_i,sigmoid$组成，可以看成和forget gate结构一样，但是彼此不共享参数。
    • 其结构图如下所示，$\widehat{C_i}$表示一个新的cell state候选值，其和$i_i$点乘从而决定哪些信息应该被加入新的cell state中。
      
    • 数学公式表示：$i_i=sigmoid(W_{ih}{h}_{i-1}+W_{ix}{x}_i),\widehat{C_i}=tanh(W_{ch}{h}_{i-1}+W_{cx}{x}_i)$。而这里为什么使用tanh还有待探索。tanh相对于sigmoid是0均值的。
  • update gate：更新Cell state
    • 其是对f和C作点乘，得到过滤掉信息的C，再对其加上因为本次输入需要添加的信息。
    • 结构图如下所示
      
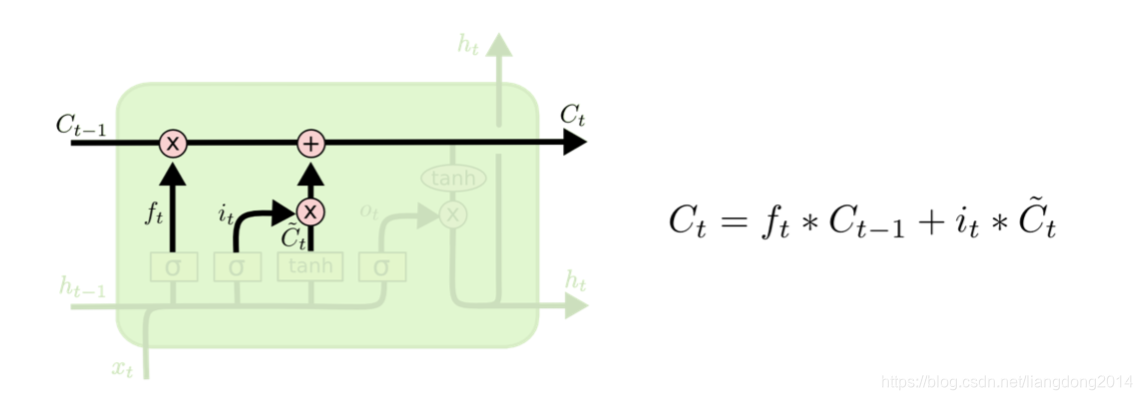
    • 数学公式表示：$C_i=C_{i-1}\ast f_i+i_i\ast {\hat{C}}_i$，前者表示删去应该遗忘的信息后保存下来的信息，后者表示应该加上去的信息。
  • output gate：生成我们的hidden state
    • 其是由h_{i-1}, x_i 和 cell state的非线性映射进行点积运算得到的。
    • 其网络结构图如下所示：
      
    • 数学表示：$h_i=sigmoid(W_{oh}{h}_{t-1}+W_{ox}{x}_i)\ast tanh(C_i)$
  • 其是怎么解决在recurrent过程中出现的梯度消失问题呢？
    • 简单来说，在对$W_{oh},W_{ox}$计算导数的过程中，我们的$W_{oh},W_{ox}$计算导数就会有两部分，前者是连城，后者是加分，有一个C在里面，加分从而避免了梯度消失。比如 $h_i=sigmoid(W_{oh}{h}_{i-1}+W_{ox}{x}_i)\ast tanh(C_i)=sigmoid(W_{oh}(sigmoid(W_{oh}{h}_{i-2}+W_{ox}{x}_{i-1})\ast tanh(C_{i-1}))+W_{ox}{x}_i)\ast tanh(C_i)$
    • 复杂来讲有待探索。。

GRU (Gated recurrent unite)

• 我们上面讲了LSTM是如何的结构，接下来我们看一下GRU是怎么样的结构。
• 相对于LSTM的cell，GRU相对能简单一些。
  • 首先GRU没有cell state的概念，它将信息一直保存在hidden state中。
  • 其次，最后GRU的输出也是由两部分组成，一部分是上一层hidden state保存下来的有用信息(第一部分)，一部分是这层新的hidden hidden state应该被加入的信息(两者取并集)(第二部分)。
    
  • GRU由update gate，reset gate，current content gate，output gate四部分组成。
  • update gate：决定上一个hideen state中哪些信息应该被保留，有点像LSTM中的forget gate
    • 其结构图如下所示：
      
    • 公式化：$z_t=W_{zh}{h}_{t-1}+W_{zx}{x}_t$
  • reset gate:决定上一个state 的哪些信息应该被重置。他与update gate不同的是，update gate主要是用在第一部分。而这里的reset gate主要用在生成第二部分。
    • 其网络结构图如下所示：
      
    • 其网络结构和update gate基本一致，不共享参数，拥有相同结构。
    • 数学公式表达：$r_t=W_{rh}{h}_{t-1}+W_{rx}{x}_t$
  • current content gate: 主要是生成本cell的state(注意和输出的state不同，更“隐蔽“，有点像LSTM 里面的cell state)。
    • 其结构如下所示：
      
    • 使用当前的输x_t, 和经过reset gate处理过的上一cell的state的组合得到本cell的state。
    • 公式化如下：$h_t^{\prime }=tanh(Wx+r_t\ast h_{t-1})$
  • output gate:输出门，将update后的上一个state和本时刻的state相结合。
    • 其网路结构如下所示：
      
    • 注意，我们在这里相当于重用了$z_t$，使用$1-z_t$就表示要强化update后的上一个时刻没有的信息。
    • 公式化表达：$h_t=z_t\ast h_i+(1+z_t)\ast h_i^{\prime }$

对比LSTM和GRU

• 相似点：
  • 他们相比于传统的RNN，他们都引入了新的gate。
  • 在更新memory content的时候，他们都是原有的content+新生成的content的形式。也就是说他们都会create 一个hidden的hidden new memory content，用这个content和previous content相加，得到最后的content。例如GRU：$h_t=z_t\ast h_i+(1+z_t)\ast h_i^{\prime }$；LSTM：$C_i=C_{i-1}\ast f_i+i_i\ast {\hat{C}}_i$
• 不同点：
  • 在向下一层传递state的时候，LSTM比GRU多了一个control gate。对比起来GRU：$h_t=z_t\ast h_i+(1+z_t)\ast h_i^{\prime }$，而LSTM：$h_i=sigmoid(W_{oh}{h}_{t-1}+W_{ox}{x}_i)\ast tanh(C_i)$，前面的sigmoid就是多出来的control gate。体现在LSTM Cell的结构图是就如下所示：
    
  • 第二点不同就是在更新state的时候，针对新生成的memory content，LSTM也比GRU多了一个control gate。用来控制哪些元素应该被用来更新。体现在公式上， GRU：$h_t^{\prime }=tanh(Wx+r_t\ast h_{t-1})$，LSTM：$C_i=C_{i-1}\ast f_i+i_i\ast {\hat{C}}_i$。体现在LSTM Cell的结构图上就如下图所示
    

参考文献

1. How RNN work
2. Understanding LSTM
3. Understanding GRU
4. Different between GRU and LSTM