基础知识
树的定义:
树是n (n≥1) 个结点的有限集合T,并且满足
- 有一个被称之为根(root)的结点
- 其余的结点可分为m(m≥0)个互不相交的集合Tl,T2,…,Tm,这些集合本身也是一棵树,也有自己的根结点,它们被称为根结点的子树(Subree)。
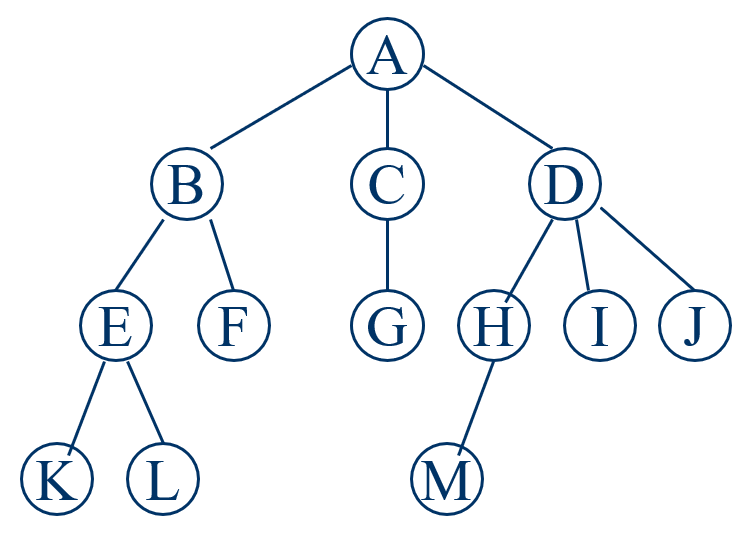
树结构中的概念
- 有序树:计算机的存储是有序的,为方便计算机处理,往往把子结点按从左到右的次序顺序编号,即把树作为有序树(ordered tree)看待。(结点的子树在树中的位置固定,不能互换)
- 在有序树中,最左边的子树的根称为第一个孩子(左孩子),最右边的称为最后一个孩子(右孩子)。
- 某个结点的孩子节点个数称为这个结点的度,树中结点的最大度数称为树的度。
树的性质

注:n1为度为1的结点个数,以此类推。ceil意为向上取整。
树的常用操作
- create():创建一棵空树;
- clear():删除树中的所有结点;
- IsEmpty():判别是否为空树;
- root():找出树的根结点。如果树是空树,则返回一个特殊的标记;
- parent(x):找出结点x的父结点;
- child(x,i):找结点x的第i个子结点;
- delete(x,i):剪枝,删除结点x的第i棵子树;
- MakeTree(x,T1, T2, ……,Tn):建一棵以x为根结点,T1, T2, ……,Tn为第i棵子树的树;
- 遍历traverse():访问树上的每一个结点。
二叉树
定义:
二叉树(Binary Tree)是结点的有限集合,它或者为空,或者由一个根结点及两棵互不相交的左、右子树构成,而其左、右子树又都是二叉树。
注意:二叉树必须严格区分左右子树。即使只有一棵子树,也要说明它是左子树还是右子树。交换一棵二叉树的左右子树后得到的是另一棵二叉树。
二叉树的分类
满二叉树
- 任意一层的结点个数都达到了最大值
- 一棵高度为k并具有2^k-1个结点的二叉树称为满二叉树。
完全二叉树
- 在满二叉树的最底层自右至左依次(注意:不能跳过任何一个结点)去掉若干个结点得到的二叉树也被称之为完全二叉树。满二叉树一定是完全二叉树,但完全二叉树不一定是满二叉树。
- 完全二叉树的特点是:
- 所有的叶结点都出现在最低的两层上
- 对任一结点,如果其右子树的高度为k,则其左子树的高度为k或k+1
二叉树的性质
- 一棵非空二叉树的第i层上最多有2^(i-1)个结点(i≥1)
- 一棵高度为k的二叉树,最多具有2^k-1个结点。
- 对于一棵非空二叉树,如果叶子结点数为n0,度数为2的结点数为n2,则有: n0=n2+1
- 具有n个结点的完全二叉树的高度 k = floor(log2n) + 1
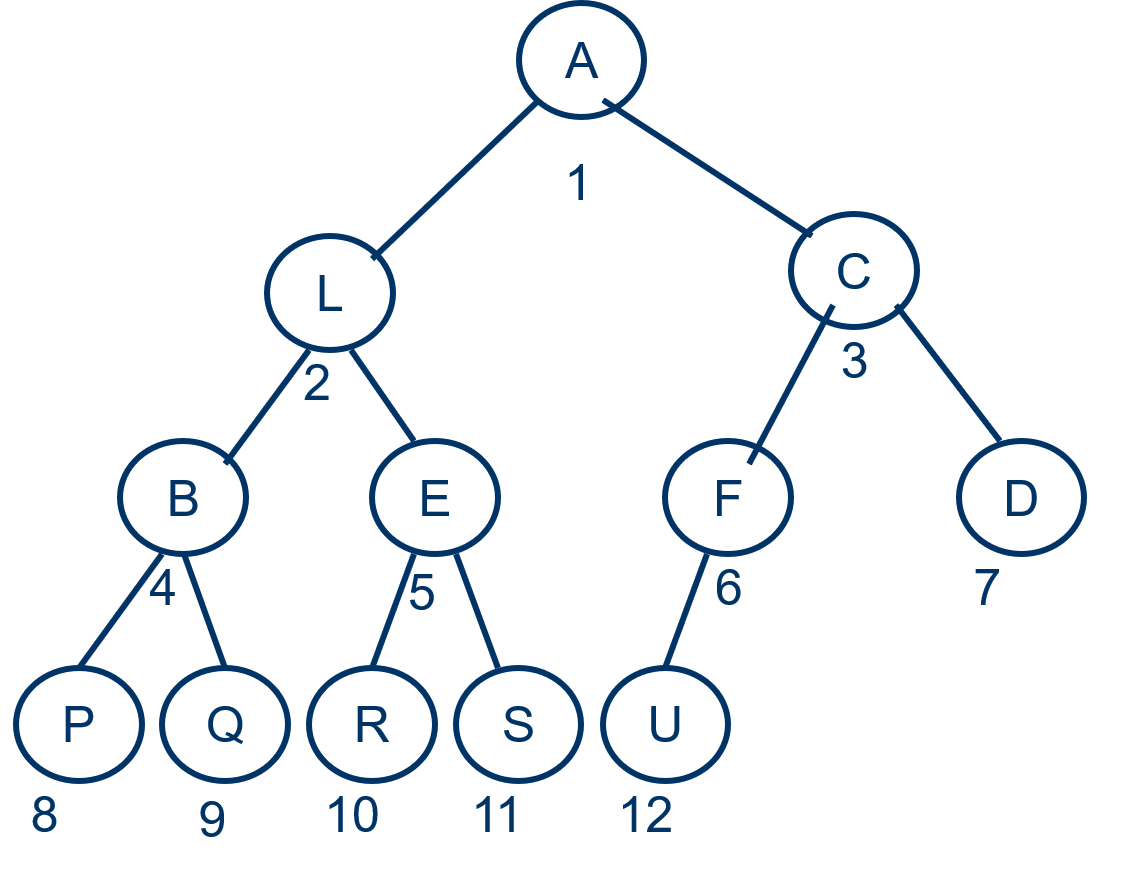
- 如果对一棵n个结点的完全二叉树的结点按层自上而下,每一层按自左至右依次编号。若设根结点的编号为1。则对任一编号为i的结点(1≤i≤n),有:
- 如果i=1,则该结点是二叉树的根结点;如果i>1,则其父亲结点的编号为floor(i/2)。
- 如果2i > n,则编号为i的结点为叶子结点,没有儿子,或其左儿子的编号为2i。
- 如果2i + 1 > n,则编号为i的结点无右儿子,或其右儿子的编号为2i+1。
二叉树的常用操作
- create():创建一棵空的二叉树;
- clear():删除二叉树中的所有结点;
- IsEmpty():判别二叉树是否为空树;
- root():找出二叉树的根结点。
- parent(x):找出结点x的父结点;
- lchild(x):找结点x的左孩子结点;
- rchild(x):找结点x的右孩子结点;
- delLeft(x):删除结点x的左子树;
- delRight(x):删除结点x的右子树;
- MakeTree(x,TL, TR):构建一棵以x为根结点,以TL, TR为左右子树的二叉树;
- traverse():访问二叉树上的每一个结点。
二叉树的遍历
二叉树的遍历讨论的是如何访问到树上的每一个结点:在线性表中,我们可以沿着后继链访问到所有结点。而二叉树是有分叉的,因此在分叉处必须确定下一个要访问的节点:是根结点、左结点还是右结点
根据不同的选择,有三种遍历的方法:前序、中序和后序
如果二叉树为空,则操作为空,否则
- 前序遍历:访问根结点->前序遍历左子树->前序遍历右子树
- 中序遍历:中序遍历左子树->访问根结点->中序遍历右子树
- 后序遍历:后序遍历左子树->后序遍历右子树->访问根结点
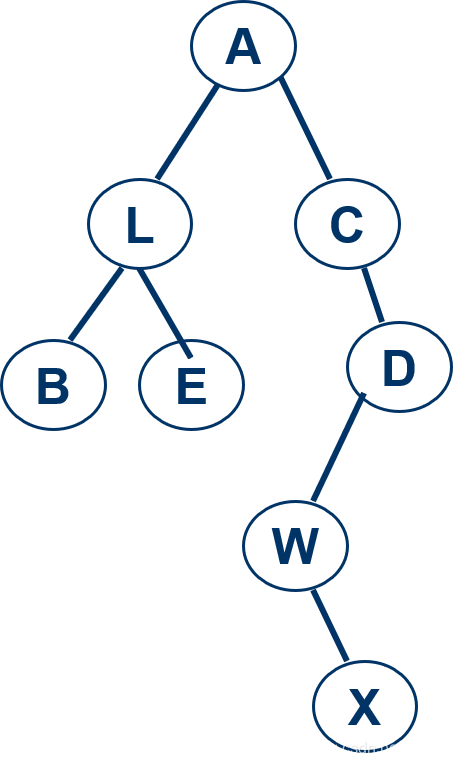
例如要遍历上面的二叉树
- 前序:A、L、B、E、 C、D、W、X
- 中序:B、L、E、A、 C、W、X、D
- 后序:B、E、L、X、 W、D、C、A
二叉树的实现
顺序实现
- 注意:如果是非完全二叉树,需要将其修补为完全二叉树
- 特点:
- 存储空间的浪费。
- 一般只用于一些特殊的场合,如静态的并且结点个数已知的完全二叉树或接近完全二叉树的二叉树。
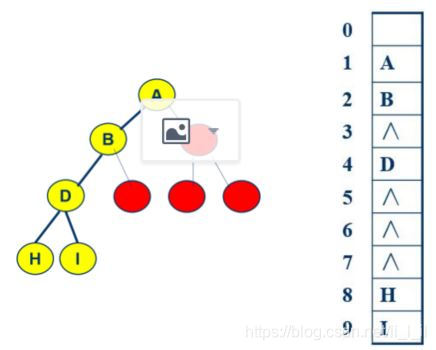
链接实现
标准形式
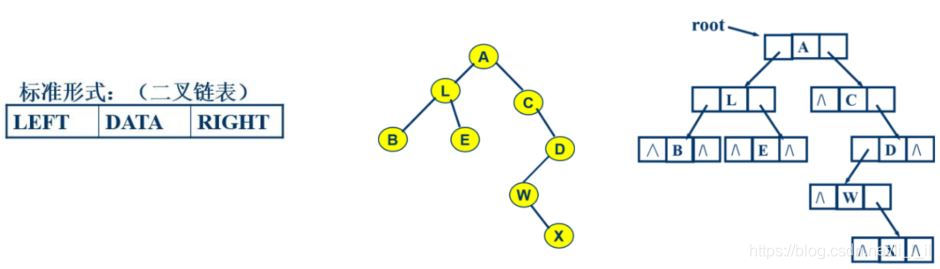
二叉树的基本运算
注意:由于二叉树是一个递归的结构,因此二叉树中的许多运算的实现都是基于递归函数
- create():将指向根结点的指针设为空指针就可以了,即root = NULL。
- isEmpty():只需要判别root即可。如果root等于空指针,返回true,否则,返回false。
- root():返回root指向的结点的数据部分。如果二叉树是空树,则返回一个特殊的标记。
- lchild(x):返回结点x的left值
- rchild(x):返回结点x的right值
- delLeft(x):对左子树调用clear函数删除左子树,然后将结点x的left置为NULL。
- delRight(x):对右子树调用clear函数删除右子树,然后将结点x的right置为NULL
- makeTree(x,TL, TR):为x申请一个结点,让它的left指向TL的根结点,right指向TR的根结点。
- clear() :根结点的删除:回收根结点的空间,把指向根结点的指针设为空指针;左子树和右子树的删除:和整棵树的删除过程是一样:
- If (左子树非空) 递归删除左子树;
- If (右子树非空) 递归删除右子树;
- delete root指向的结点;
- root = NULL;
代码实现
大多数情况下,二叉树都是用二叉链表实现,所以仅介绍用二叉链表实现的二叉树类。
标准的链接存储由两个类组成:结点类和树类
- 节点Node:
- 数据成员包括:结点的数据及左右孩子的指针。
- 操作包括:构造和析构
- 二叉树类:
- 树的存储:存储指向根结点的指针
- 操作:树的标准操作加了一个建树的函数
- 递归函数的设计
- 对于二叉树类的用户来说,他并不需要知道这些操作时用递归函数实现的。对用户来说,调用这些函数并不需要参数,但递归函数必须有一个控制递归终止的参数。设计时,我们将用户需要的函数原型作为公有的成员函数。每个公有成员函数对应一个私有的、带递归参数的成员函数。公有函数调用私有函数完成相应的功能。
树类
template <class Type>
class BinaryTree {
private:
struct Node {
Node *left, *right; // 结点的左、右儿子的地址
Type data; // 结点的数据信息
Node() : left(NULL), right(NULL) { }
Node(Type item, Node *L = NULL, Node * R = NULL) :data(item), left(L), right(R) {}
~Node() {}
};
Node *root; // 二叉树的根结点。
public:
BinaryTree() : root(NULL) {} // 构造空二叉树
BinaryTree(const Type & value) {root = new Node(value);} //非空二叉树构造函数
~BinaryTree() { clear(); }
Type getRoot() const {return root->data;} //返回根节点的数据
Type getLeft() const {return root->left->data;} //返回右子树节点的数据
Type getRight() const {return root->right->data;} //返回左子树节点的数据
void makeTree(const Type &x, BinaryTree <,BinaryTree &rt) //构建一棵以x为根结点,以TL, TR为左右子树的二叉树;
{
root = new Node(x, lt.root, rt.root);
lt.root = NULL;
rt.root = NULL;
}
void delLeft() //删除左子树
{
BinaryTree tmp = root->left;
root->left = NULL;
tmp.clear();
}
void delRight() //删除左子树
{
BinaryTree tmp = root->right;
root->right = NULL;
tmp.clear();
}
void clear() //清空树
{
if (root != NULL) clear(root);
root = NULL;
}
bool isEmpty() const { return root == NULL; } //判空
int size() const { return size(root); } //节点数
int height() const { return height(root); } //高度
void preOrder() const {
if (root != NULL) {
cout << "\n前序遍历:";
preOrder(root);
}
};
void postOrder() const {
if (root != NULL) {
cout << "\n后序遍历:";
postOrder(root);
}
};
void midOrder() const {
if (root != NULL) {
cout << "\n中序遍历:";
midOrder(root);
}
};
void createTree(Type flag);
private:
int height(Node *t) const; //计算树的高度
int size(Node *t) const; //运用递归就算节点数
void clear(Node *t);
void preOrder(Node *t) const;
void postOrder(Node *t) const;
void midOrder(Node *t) const;
};
height
template <class Type>
int BinaryTree<Type>::height(Node *t) const //计算树的高度
{
if (t == NULL) return 0;
else {
int lt = height(t->left), rt = height(t->right);
return 1 + ((lt > rt) ? lt : rt);
}
}
size
template <class Type>
int BinaryTree<Type>::size(Node *t) const //运用递归就算节点数
{
if (t == NULL) return 0;
return 1 + size(t->left) + size(t->right);
}
clear
template <class Type>
void BinaryTree<Type>::clear(Node *t)
{
if (t->left != NULL) clear(t->left);
if (t->right != NULL) clear(t->right);
delete t;
}
preOrder
template <class Type>
void BinaryTree<Type>::preOrder(Node *t) const
{
if (t != NULL) {
cout << t->data << ' ';
preOrder(t->left);
preOrder(t->right);
}
}
midOrder
template <class Type>
void BinaryTree<Type>::midOrder(Node *t) const
{
if (t != NULL) {
midOrder(t->left);
cout << t->data << ' ';
midOrder(t->right);
}
}
postOrder
template <class Type>
void BinaryTree<Type>::postOrder(Node *t) const //后序遍历
{
if (t != NULL) {
postOrder(t->left);
postOrder(t->right);
cout << t->data << ' ';
}
}
creatTree
template <class Type>
void BinaryTree<Type>::createTree(Type flag)
{
linkQueue<Node *> que; //节点队列,只用于输入
Node *tmp;
Type x, ldata, rdata;
//创建树,输入flag表示空
cout << "\n输入根结点:";
cin >> x;
root = new Node(x); //创建根节点
que.enQueue(root);
while (!que.isEmpty()) {
tmp = que.deQueue(); //根节点?
cout << "\n输入" << tmp->data
<< "的两个儿子(" << flag
<< "表示空结点):";
cin >> ldata >> rdata;
if (ldata != flag)
que.enQueue(tmp->left = new Node(ldata));
if (rdata != flag)
que.enQueue(tmp->right = new Node(rdata));
}
cout << "create completed!\n";
}
遍历的非递归实现
前序遍历
方法:把二叉树的根结点存入栈中。然后重复以下过程,直到栈为空:
- 从栈中取出一个结点,输出根结点的值;
- 然后把右子树,左子树放入栈中
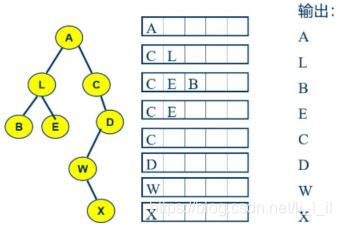
代码
template <class Type>
void BinaryTree<Type>::preOrder() const
{ linkStack<Node *> s;
Node *current;
cout << "前序遍历: ";
s.push( root );
while ( !s.isEmpty() ) {
current = s.pop();
cout << current->data;
if ( current->right != NULL ) s.push( current->right );
if ( current ->left != NULL ) s.push( current->left );
}
}
中序遍历
方法:中序遍历中,先要遍历左子树,接下去才能访问根结点,因此,当根结点出栈时,我们不能访问它,而要访问它的左子树,此时要把树根结点暂存一下。由于左子树访问完后还要访问根结点,因此仍可以把它存在栈中,接着左子树也进栈。此时执行出栈操作,出栈的是左子树。左子树访问结束后,再次出栈的是根结点,此时根结点可被访问。根结点访问后,访问右子树,则将右子树进栈。
栈元素的设计
- 在中序遍历中根结点要进栈两次。
- 当要遍历一棵树时,将根结点进栈。
- 根结点第一次出栈时,它不能被访问,必须重新进栈,并将左子树也进栈,表示接下去要访问的是左子树。
- 根结点第二次出栈时,才能被访问,并将右子树进栈,表示右子树可以访问了。
- 在中序遍历时不仅要记住需要访问哪一棵树,而且还必须记住根结点是在第几次进栈。
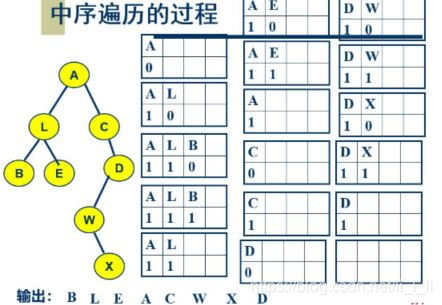
栈元素定义代码
struct StNode
{
Node *node;
int TimesPop;
StNode ( Node *N = NULL ):node(N), TimesPop(0) { }
};
中序遍历非递归实现
template <class Type>
void BinaryTree<Type>::midOrder() const
{ linkStack<StNode> s;
StNode current(root);
cout << "中序遍历: ";
s.push(current);
while (!s.isEmpty()) {
current = s.pop();
if ( ++current.TimesPop == 2 ) {
cout << current.node->data;
if ( current.node->right != NULL )
s.push(StNode(current.node->right ));}
else { s.push( current );
if ( current.node->left != NULL )
s.push(StNode(current.node->left) );
}
}
}
后序遍历
思路:将中序遍历的非递归实现的思想进一步延伸,可以得到后序遍历的非递归实现。当以后序遍历一棵二叉树时,先将树根进栈,表示要遍历这棵树。根结点第一次出栈时,根结点不能访问,应该访问左子树。于是,根结点重新入栈,并将左子树也入栈。根结点第二次出栈时,根结点还是不能访问,要先访问右子树。于是,根结点再次入栈,右子树也入栈。当根结点第三次出栈时,表示右子树遍历结束,此时,根结点才能被访问。
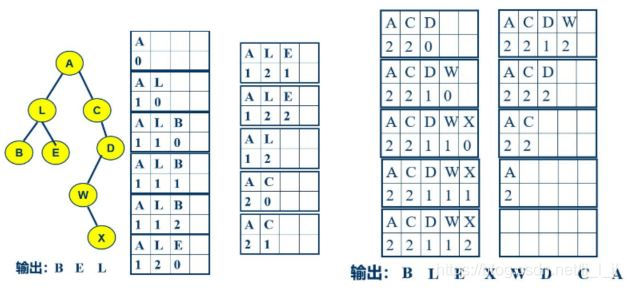
代码
template <class Type>
void BinaryTree<Type>::postOrder() const
{
linkStack< StNode > s;
StNode current(root);
cout << "后序遍历: ";
s.push(current);
while (!s.isEmpty())
{ current = s.pop();
if ( ++current.TimesPop == 3 )
{cout << current.node->data; continue;}
s.push( current );
if ( current.TimesPop == 1 )
{ if ( current.node->left != NULL )
s.push(StNode( current.node->left) );
}
else {
if ( current.node ->right != NULL )
s.push(StNode( current.node->right ) );
}
}
}
























 1407
1407

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








