算法设计与分析实验六：分支限界法

一、实验目的

1、深入理解分支限界法的剪枝搜索策略。

2、掌握分支限界法解题的算法框架。

3、学习并理解分支限界法的设计策略。

二、问题描述

假设有n个任务由k个可并行工作的机器完成，完成任务i需要的时间为ti。设计一个算法找出完成这n个任务的最佳调度，使得完成全部任务的时间最早。

算法设计：对任意给定的整数n和k，以及完成任务i需要的时间为ti（i=1~n）。设计一个优先队列式分支界限界法，计算完成这n个任务的最佳调度。

• 输入

第一行有2 个正整数n和k。第2 行的n个正整数是完成n个任务需要的时间。

如

7 3

2 14 4 16 6 5 3

• 输出

输出计算的完成全部任务的最早时间。

上例输出为

17

• 数据结构

物理存储结构：顺序存储结构

数据的基本操作：遍历，查找

方法：分支限界法递归

六、算法设计

#include<bits/stdc++.h>

 using namespace std;

  int n,k;

  int x[100];//机器

  int x1[100];//作业

  int maxnum=1000000;

  void task(int sp)

  {

     if(sp>n){

      int temp=0;

      for(int i=1;i<=k;i++){

        if(x[i]>temp){

            temp=x[i];

         }

      }

      if(temp<maxnum){

         maxnum=temp;

      }

     }

     else{

         for(int i=1;i<=k;i++){

             x[i]+=x1[sp];

             task(sp+1);

             x[i]-=x1[sp];

         }

     }

 }

 int main()

 {

     cin >> n;

     cin >> k;

     for(int i=1;i<=n;i++){

         cin >>x1[i];

     }

     task(1);

     cout << maxnum;

     return 0;

 }

七、实验结果

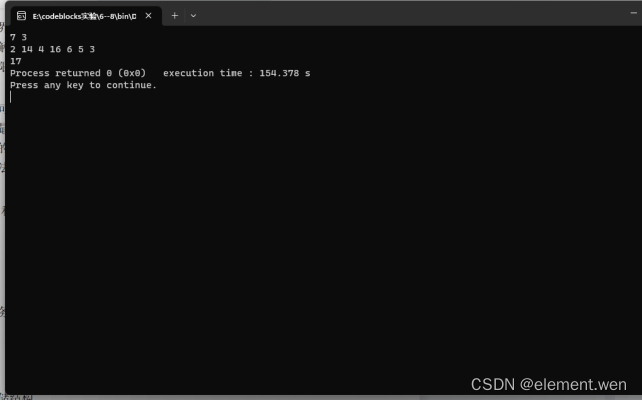
八、实验心得

通过这次实验我理解了分支限定法采用广度优先方法，以最小耗费优先方式搜索解空间树，求解目标是找出满足约束条件的一个解，是从众多分支的路径中，同时地毯式搜索找到符合结果的路径或路径集的方法。