问题的引入
已知某种材料在生产过程中的废品率 y 与某种化学成分x 有关,下列表中记载了 某工厂生产中y 与相应的x 几次数值:

我们想找出 y 对 x 的一个近似公式。
把表中数值画出图来看,发现它的变化趋势近似于一条直线。 因此我们决定选取 x 的一次式ax+b来表示,当然最好能选择适当的 a,b,使下面的等式都成立。

实际上一般是不可能的,任何a,b代入上面各式都会发生误差。于是想找a,b使上面各式的误差的平方和最小,即

最小. 这里讨论的误差的平方即二乘方,故称为最小二乘法. 现在转向一般的最小二乘法问题:

可能无解,即任何一组数x1 , x2 ,…,xn 都可能使

我们设法找到实数组x1 , x2 ,…,xn 使上式最小。这样的实数组x1 , x2 ,…,xn称为最小二乘解,这种问题称为最小二乘法问题。
最小二乘的推到
定理:X=(x1 , x2 ,…,xn)T是矛盾方程组(1)的最小二乘解的充要条件是X是方程组


上式用欧氏空间中向量的距离表示就是

最小二乘法就是找x1 , x2 ,…,xn 使Y 与B距离短.
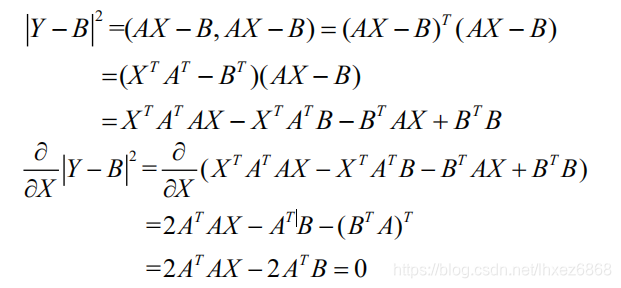
最小二乘解所满足的矩阵(代数)方程是

这是一个线性方程组,系数矩阵是,常数项是
。
推导过程用到的向量的求导公式
向量对向量偏导公式

标量对向量偏导公式

实际问题示例
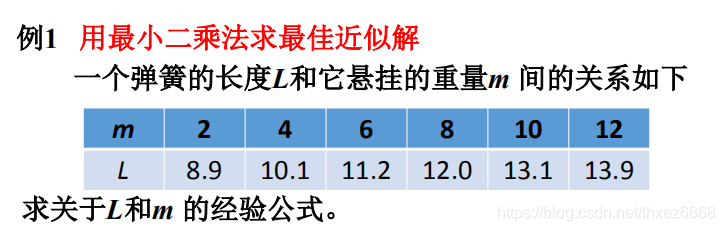



总结
找不到一组参数的解满足方程组时,设法让方程与结果的误差平方和最小,这就是最小二乘的核心思想,最终求得x的解
,当
不存在的时候考虑优化。
- 是否存在多种因素,去掉不别要的因素;
- 去掉共线因素;
- 舍弃点精确度,加上一个单位矩阵使逆存在,
。
























 1665
1665

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








