2019牛客暑期多校训练营（第五场）I——three points 1（计算几何）

链接：https://ac.nowcoder.com/acm/contest/885/I
来源：牛客网
 

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
Special Judge, 64bit IO Format: %lld

题目描述

You are given five positive integers w, h, a, b, c. Please construct 3 points X, Y, Z in the 2-dimensional plane such that the distance between X and Y is a, the distance between X and Z is b, the distance between Y and Z is c. Furthermore, the x coordinates of all constructed points must be in the range [0, w], and the y coordinates of all constructed points must be in the range [0,h].

The value of the constructed coordinates X, Y, Z can be real numbers. The input guarantees that at least one solution exists.

输入描述:

The first line contains an integer T indicating there are T tests.
Each test consists of a single line containing five integers: w, h, a, b, c.

1≤w,h,a,b,c≤501 \le w, h, a, b, c \le 501≤w,h,a,b,c≤50

1≤T≤5×1041 \le T \le 5 \times 10^41≤T≤5×104

输出描述:

For each test, output one line containing six numbers, the first two numbers are the coordinate of X, the third and fourth numbers are the coordinate of Y, the last two numbers are the coordinate of Z. If there are multiple solutions, please output any one.

All absolute error within 1e−61e^{-6}1e−6 will be ignored.

示例1

输入

复制

3
24 16 20 25 15
1 1 1 1 1
50 50 1 2 3

输出

复制

0.000000000000 0.000000000000 12.000000000000 16.000000000000 24.000000000000 7.000000000000
0.000000000000 0.000000000000 0.500000000000 0.866025403784 1.000000000000 0.000000000000
1.000000000000 0.000000000000 0.000000000000 0.000000000000 3.000000000000 0.000000000000

说明

For the last test, the distance between (1, 0) and (0, 0) is 1, the distance between (1, 0) and (3, 0) is 2, and the distance between (0, 0) and (3, 0) is 3.

题意：在0-w，0-h的矩形中找三个点(x,y,z)，这里我用(0,1,2)代替，使他们的距离满足(0,1)=a, (0,2)=b, (1,2)=c

题解：画画图就知道了，先固定两个点，直接通过公式找第三个点，关键是怎么固定2个点，让第三个点能找的空间尽可能的大，这里有点贪心的想法，就是一个点在顶点另一个点在顶点或者边上，通过条件判定，最后通过公式找第三个点，注意：公式有误差，所以把最大范围扩大一下，我扩大的是1e-9过了，别的行不行自己试试（主要原因应该是double值比较问题）~~为了更好理解，看图，一共有6种情况~~

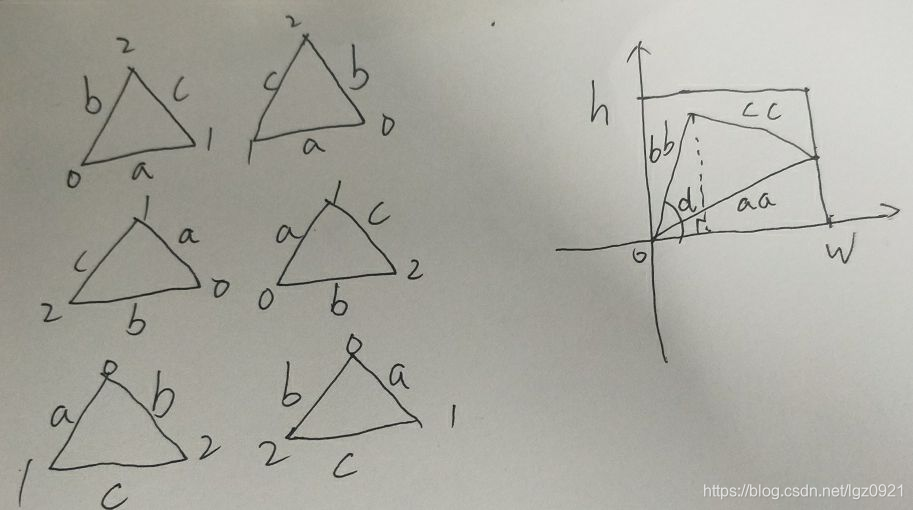
结合图片和代码就很好懂了，我看他们的代码乱七八糟，我就自己搞了搞~~~

上代码：

#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;
const double eps=1e-9;
typedef pair<double,double> par;
par f[3];
double w,h,a,b,c;
bool solve(double aa,double bb,double cc,int xx,int yy,int zz){
	f[xx]=par(0,0);
	if(aa<=w) f[yy]=par(aa,0);
    else f[yy]=par(w,sqrt(aa*aa-w*w));
    double d=acos((aa*aa+bb*bb-cc*cc)/2/aa/bb);
    d+=atan(f[yy].second/f[yy].first);//求图中的d
    f[zz]=par(bb*cos(d),bb*sin(d));
    if(f[zz].first>=0-eps&&f[zz].first<=w+eps&&f[zz].second>=0-eps&&f[zz].second<=h+eps){//扩大区间
    	printf("%.12f %.12f",f[0].first,f[0].second);
    	printf(" %.12f %.12f\n",f[1].first,f[1].second);
    	printf(" %.12f %.12f\n",f[2].first,f[2].second);
    	return true;
	}
	return false;
}
int main(){
	int t;
	scanf("%d",&t);
	while(t--){
		scanf("%lf%lf%lf%lf%lf",&w,&h,&a,&b,&c);
		if(solve(a,b,c,0,1,2)) continue;
		if(solve(a,c,b,1,0,2)) continue;
		if(solve(b,a,c,0,2,1)) continue;
		if(solve(b,c,a,2,0,1)) continue;
		if(solve(c,a,b,1,2,0)) continue;
		if(solve(c,b,a,2,1,0)) continue;
	}
	return 0;
}