时间复杂度O(n)，你绝对能成为时间管理大师

1-前言

2-算法效率

        什么是算法效率呢？，算法效率的意义究竟是什么呢？让我们来想象一个场景：某一天，小灰和大黄同时加入了一个公司…

        半天过后，小灰和大黄各自交付了代码，两端代码实现的功能都差不多。大黄的代码运行一次要花400毫秒，内存占用4MB。小灰的代码运行一次要花4秒，内存占用40MB。于是…

        由此可见，衡量代码的好坏，包括两个非常重要的指标：第一种是时间效率，第二种是空间效率。

• 时间效率被成为时间复杂度。时间复杂度主要衡量的是一个算法的运行速度
• 空间效率被称为空间复杂度。空间复杂度主要衡量一个算法所需要的额外空间

        在计算机发展的早期，计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展，计算机的存储容量已经达到了很高的程度，所以我们如今不再需要特别关注一个算法的空间复杂度。

3-时间复杂度

3-1-时间频度T(n)

        一个算法执行所耗费的时间，从理论上是不能算出来的，必须上机运行测试才能知道。但我们不可能也没有必要对每个算法都上机测试，只需知道哪个算法花费的时间多，哪个算法花费的时间少就可以了。并且一个算法花费的时间与算法中语句的执行次数成正比例，哪个算法中语句执行次数多，它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。

3-2-时间复杂度O()

        前面提到的时间频度T(n)中，n称为问题的规模，当n不断变化时，时间频度T(n)也会不断变化。但有时我们想知道它变化时呈现什么规律，为此我们引入时间复杂度的概念。一般情况下，算法中基本操作重复执行的次数是问题规模n的某个函数，用T(n)表示，若有某个辅助函数f(n)，使得当n趋近于无穷大时，T(n)/f(n)的极限值为不等于零的常数，则称f(n)是T(n)的同数量级函数，记作T(n)=O(f(n))，它称为算法的渐进时间复杂度，简称时间复杂度。

3-3-大O表示法

        像前面用O( )来体现算法时间复杂度的记法，我们称之为大O表示法。

        算法复杂度可以从最理想情况、平均情况和最坏情况三个角度来评估，由于平均情况大多和最坏情况持平，而且评估最坏情况也可以避免后顾之忧，因此一般情况下，我们设计算法时都要直接估算最坏情况的复杂度。

        大O表示法O(f(n))中的f(n)的值可以为1、n、logn、n²等，因此我们可以将O(1)、O(n)、O(logn)、O(n²)分别可以称为常数阶、线性阶、对数阶和平方阶，那么如何推导出;f(n)的值呢？我们接着来看推导大O阶的方法。

推导大O阶，我们可以按照如下的规则来进行推导，得到的结果就是大O表示法：

• 1.用常数1来取代运行时间中所有加法常数。
• 2.修改后的运行次数函数中，只保留最高阶项
• 3.如果最高阶项存在且不是1，则去除与这个项相乘的常数。

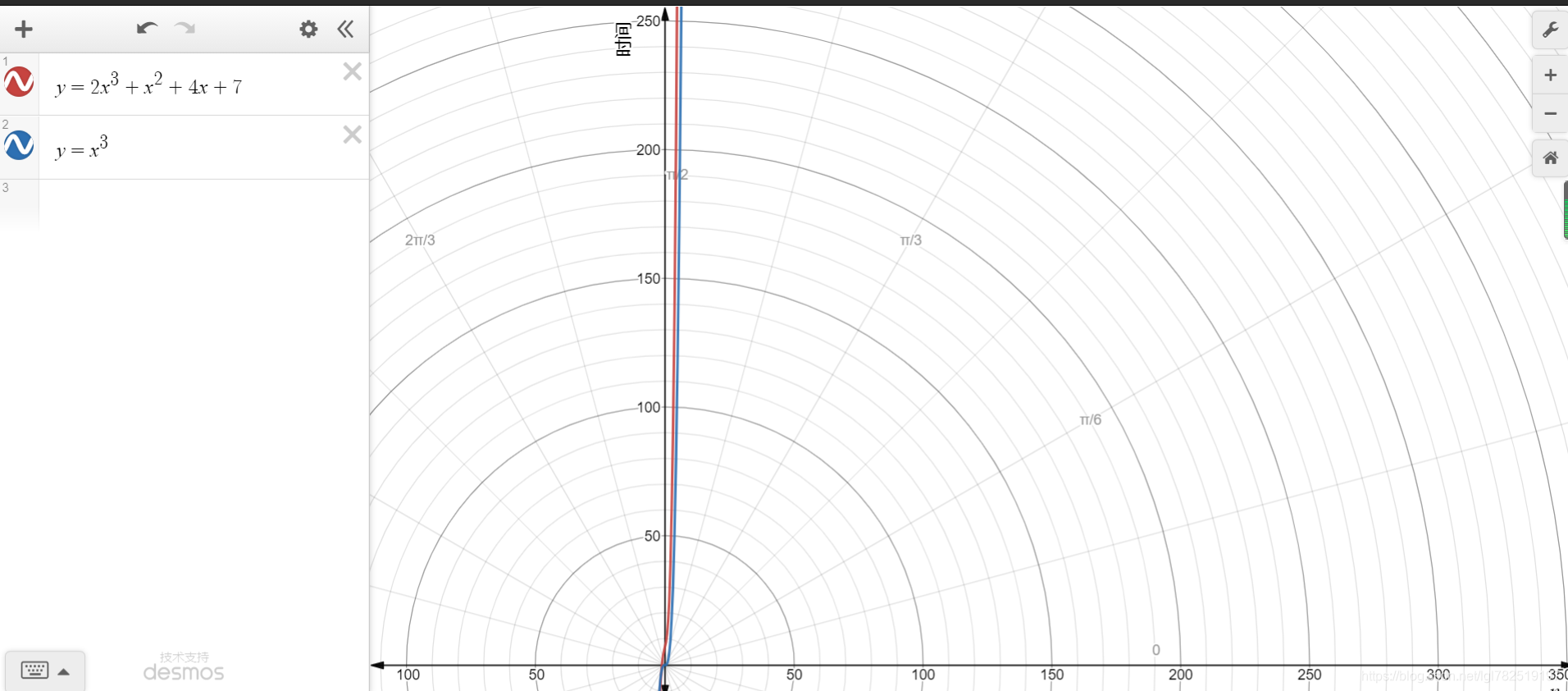
        如，假设一个算法的时间频度T(n)为T(n)=2n³+n²+4n+7，按照推到大O阶的规则，第2条，只保留最高阶项，那么我们的时间复杂度为O(2n³)，再按照第3条，那么我们的时间复杂度最终为O(n³)。

        其T(n)为T(n)=2n³+n²+4n+7和O(n³)的图像走势为

        从上面结果可以看出，我们的时间复杂度去掉了那些对结果影响不大的项，简洁明了的表示了执行次数。

4-时间复杂度举例

        为了不给大家误解，这下面所有的代数n都是正数

4-1-常数阶-O(1)

例子1

int num = 5; //执行一次
int sum = (1+num)*num/2; //执行一次
System.out.println(sum); //执行一次

        上面的代码时间频度T(n)=3，按照推到大O阶的规则第1条，那么我们的时间复杂度为O(1)，其图像走势为

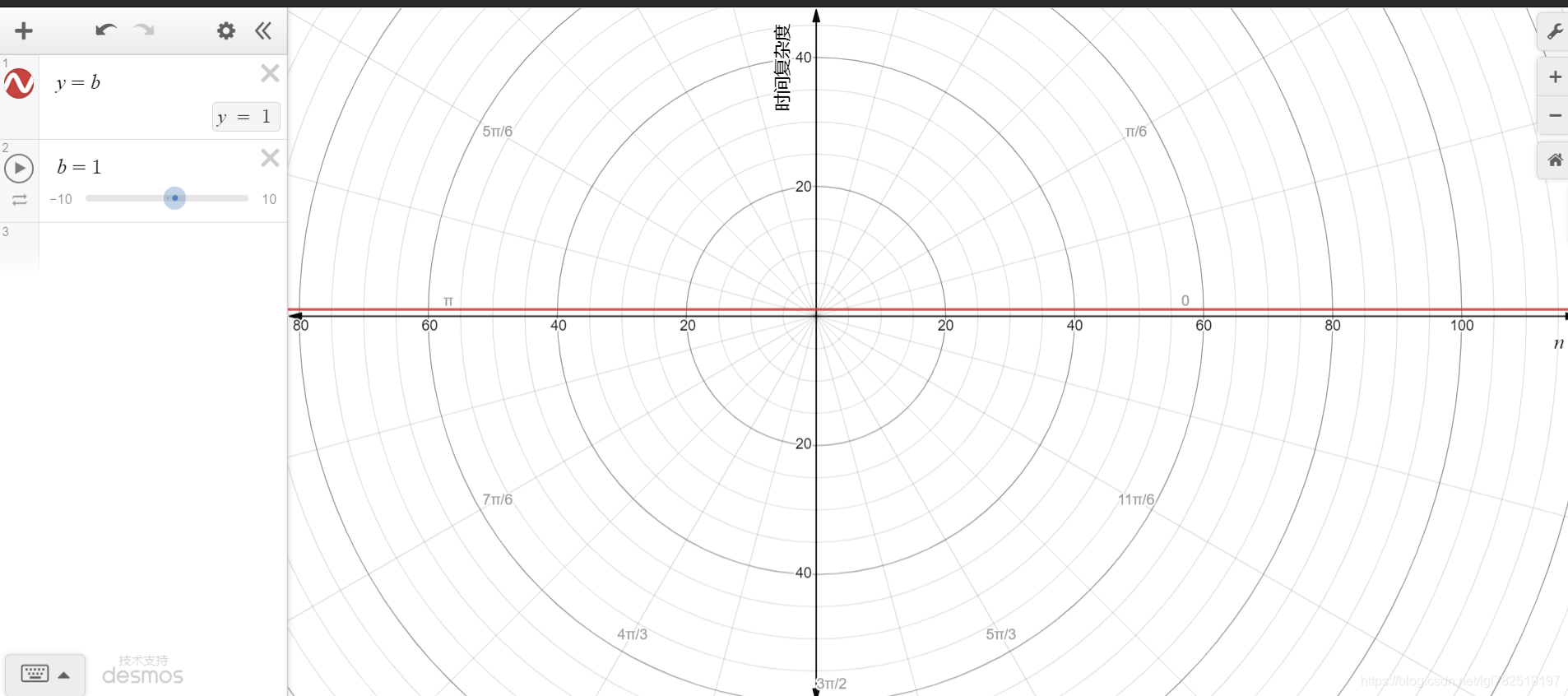
例子2

int num = 10; //执行一次
int sum = 0; //执行一次
for(int i=1;i<=num;i++){
   
   
  for(int j=i;j<=num;i++){
   
   	//内循环
      sum +=j;
  }
}
System.out.println(sum); //执行一次

        我们分析一下：由于j=i，所以
        当i=1时，内循环执行了10次
        当i=2时，内循环执行了9次
        当i=3时，内循环执行了8次
        …,…,…,…,…,…
        当i=9时，内循环执行了2次
        当i=10时，内循环执行了1次
        当i=11时，循环结束

        所以上述代码的时间频度T(n)=1+1+（10+9+8+…+2+1）+1，即T(n)=58，按照推到大O阶的规则第1条，那么我们的时间复杂度为O(1)，其图像走势为

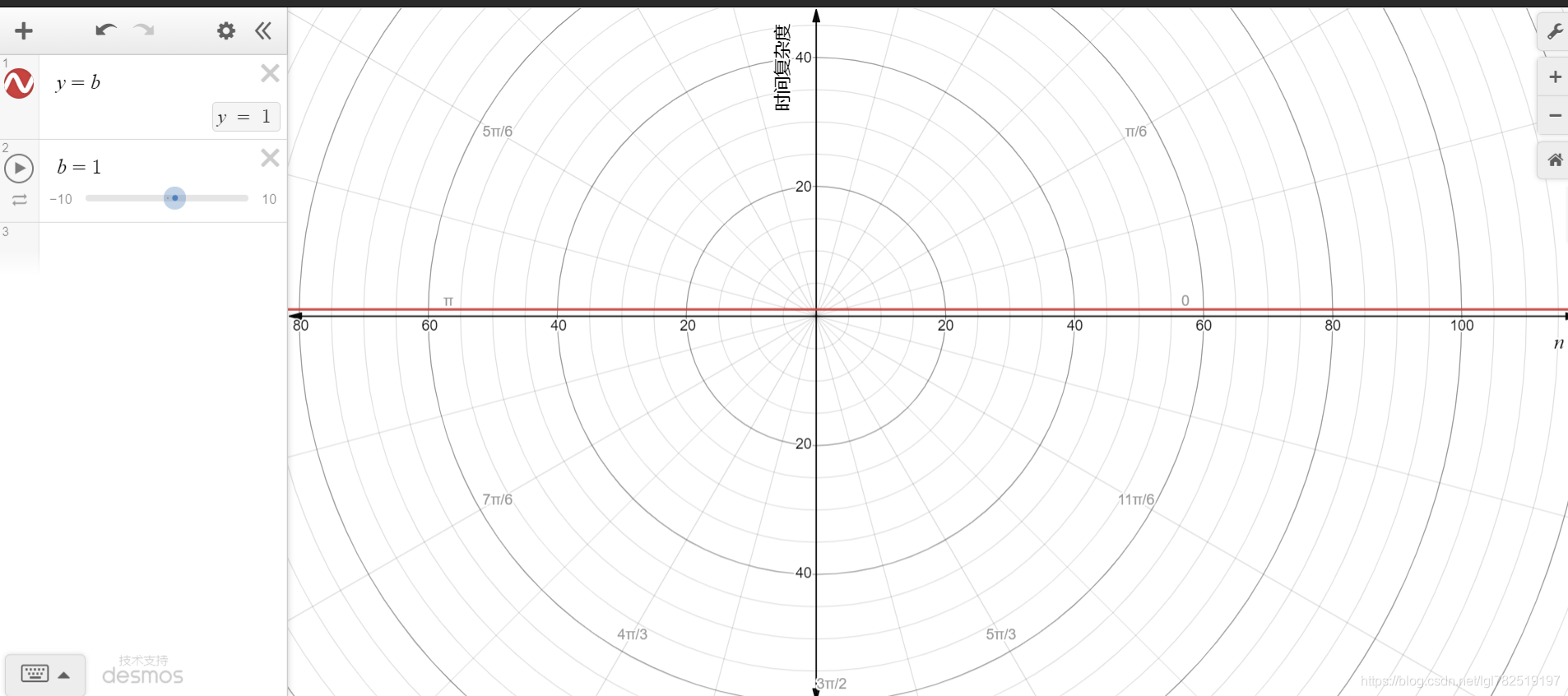
4-2-线性阶-O(n)

例子1

for(int i=0;i<n;i++){
   
   
//时间复杂度为O(1)的算法
...
}

        上面算法循环体中的代码执行了n次，因此时间复杂度为O(n)，其图像走势为

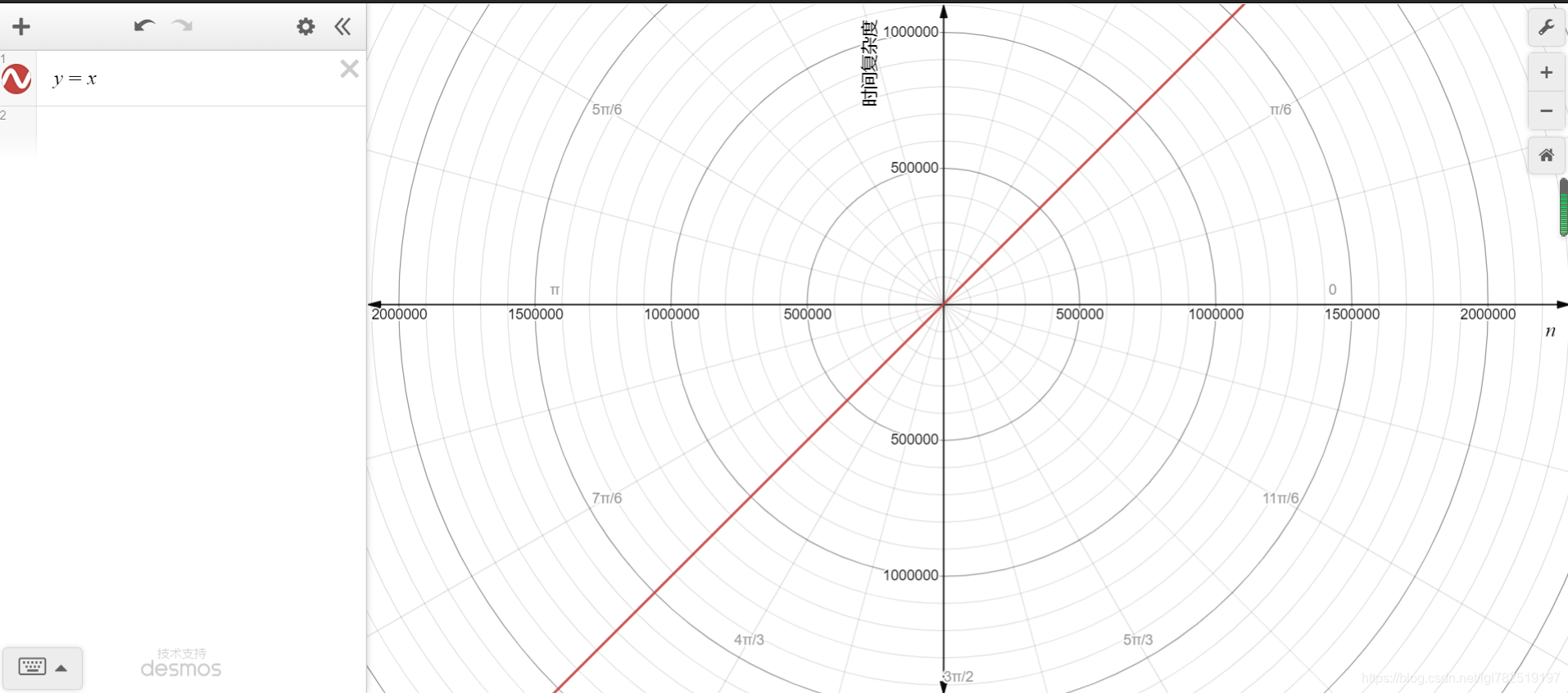
例子2

// for循环1
for(int i=0;i<n;i++){
   
   
	//时间复杂度为O(1)的算法
	...
}
// while循环1
while(n>10){
   
   
	//时间复杂度为O(1)的算法
	n--;
	...
}
// for循环2
for(int i=0;i<n-5;i++){
   
   
	//时间复杂度为O(1)的算法
	...
}

        我们分析一下：
        for循环1，代码执行了n次，此时n还是n
        while循环1，代码执行了n-10次，此时n变为10
        for循环1，代码执行了n-5次，也就是10-5=5次

        从上面的分析中，可知上述代码的时间频度T(n)=n+(n-10)+5，即T(n)=2n-5，按照推到大O阶的规则第2第3条，那么我们的时间复杂度为O(n)，其图像走势为

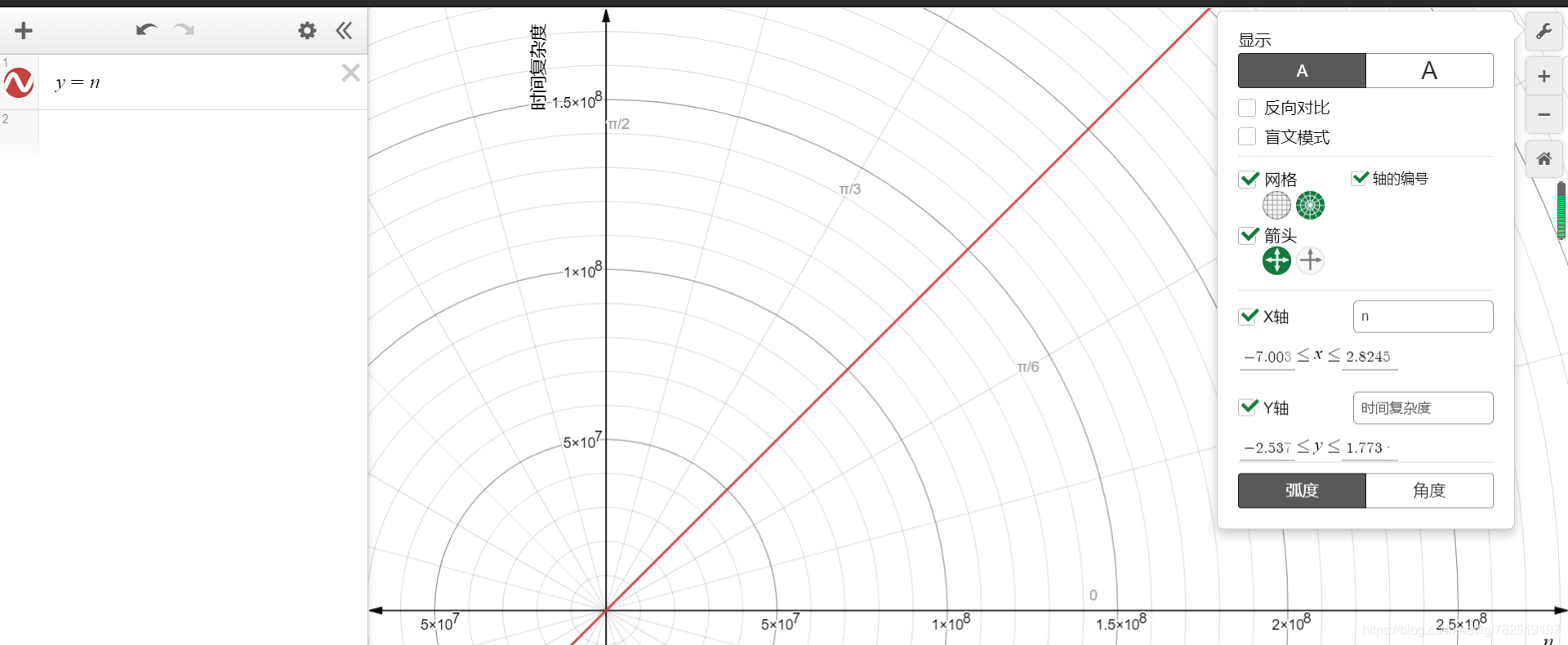
4-3-平方阶-O(n²)

例子1

for(int i=0;i<n;i++){
   
      
    for(int j=0;j<n;i++){
   
   
       //复杂度为O(1)的算法
       ... 
    }
}

        我们分析一下：
        当i=0时，内循环执行了n次
        当i=1时，内循环执行了n次
        当i=2时，内循环执行了n次
        …,…,…,…
        当i=n-2时，内循环执行了n次
        当i=n-1时，内循环执行了n次
        当i=n时，循环结束

        从上面的分析中，可知上述代码的时间频度T(n)=(n-1+1)*n，即T(n)=n²，按照推到大O阶的规则第2第3条，那么我们的时间复杂度为O(n²)，其图像走势为

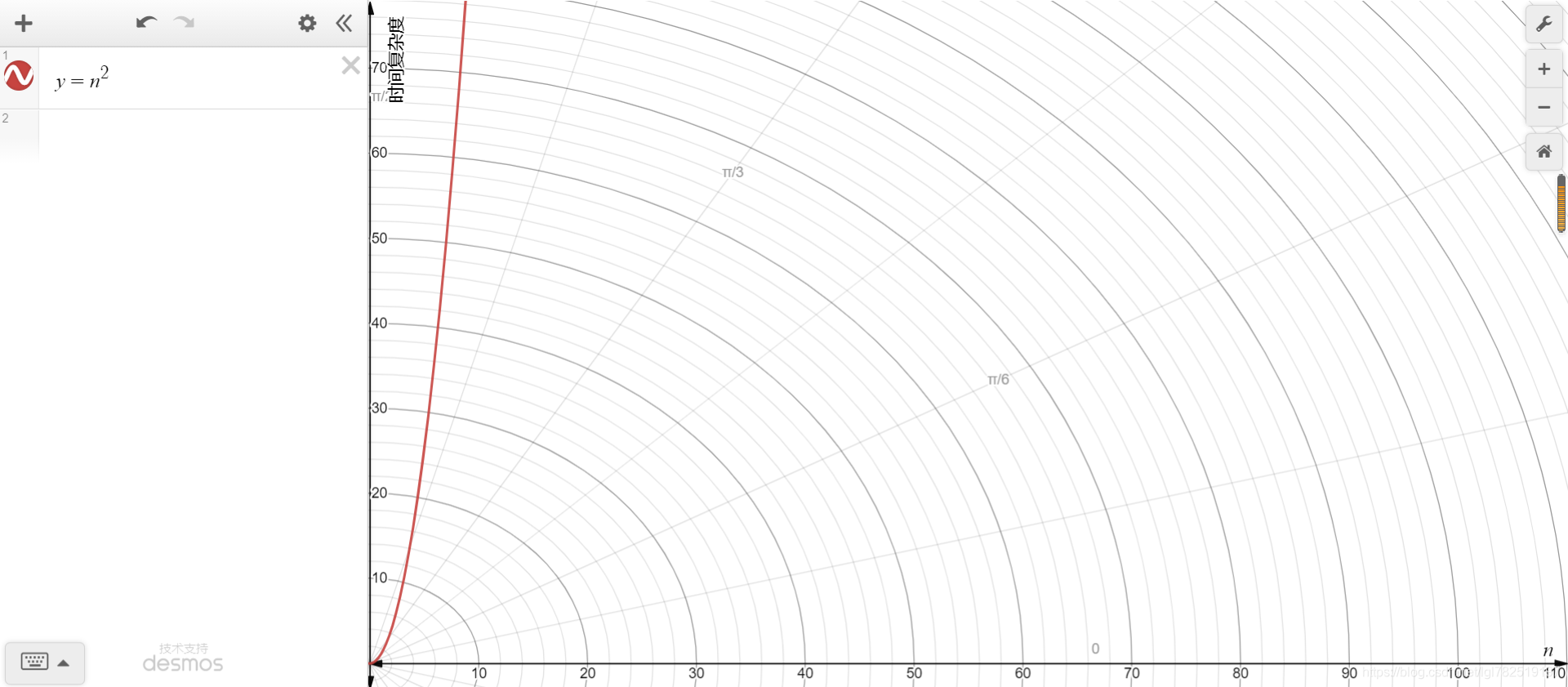
例子2，冒泡排序

// 升序
for(int i=n;i>0;i--){
   
   
     int exchange = 0;
     for(int j=1;j<i;j++){
   
   
         if(arr[j-1]>arr[j]){
   
   
         	// 交换元素
             int temp = arr[j-1];
             arr[j-1] = arr[j];
             arr[j] = temp;
             exchange = 1;
         }
     }
     if(exchange == 0){
   
   
         break;
     }
 }

        我们分析一下：

最好的情况：
 
        当数组已经排序好，如int[] arr = {1,2,3,4,5,6,7};
        那么当i=n时，内循环走了n-1次，此时arr[j-1]>arr[j]并没有触发，也就是没有元素进行交换，所以exchange == 0直接break，结束循环。

        所以T(n)=n-1，按照推到大O阶的规则第2第3条，那么我们的时间复杂度为O(n)

最坏的情况：
 
        比如数组为降序，如int[] arr = {7,6,5,4,3,2,1};
        当i=n时，内循环执行了n-1次
        当i=n-1时，内循环执行了n-2次
        当i=n-2时，内循环执行了n-3次
        …,…,…,…,…
        当i=3时，内循环执行了2次
        当i=2时，内循环执行了1次
        当i=1时，内循环没有执行，循环结束

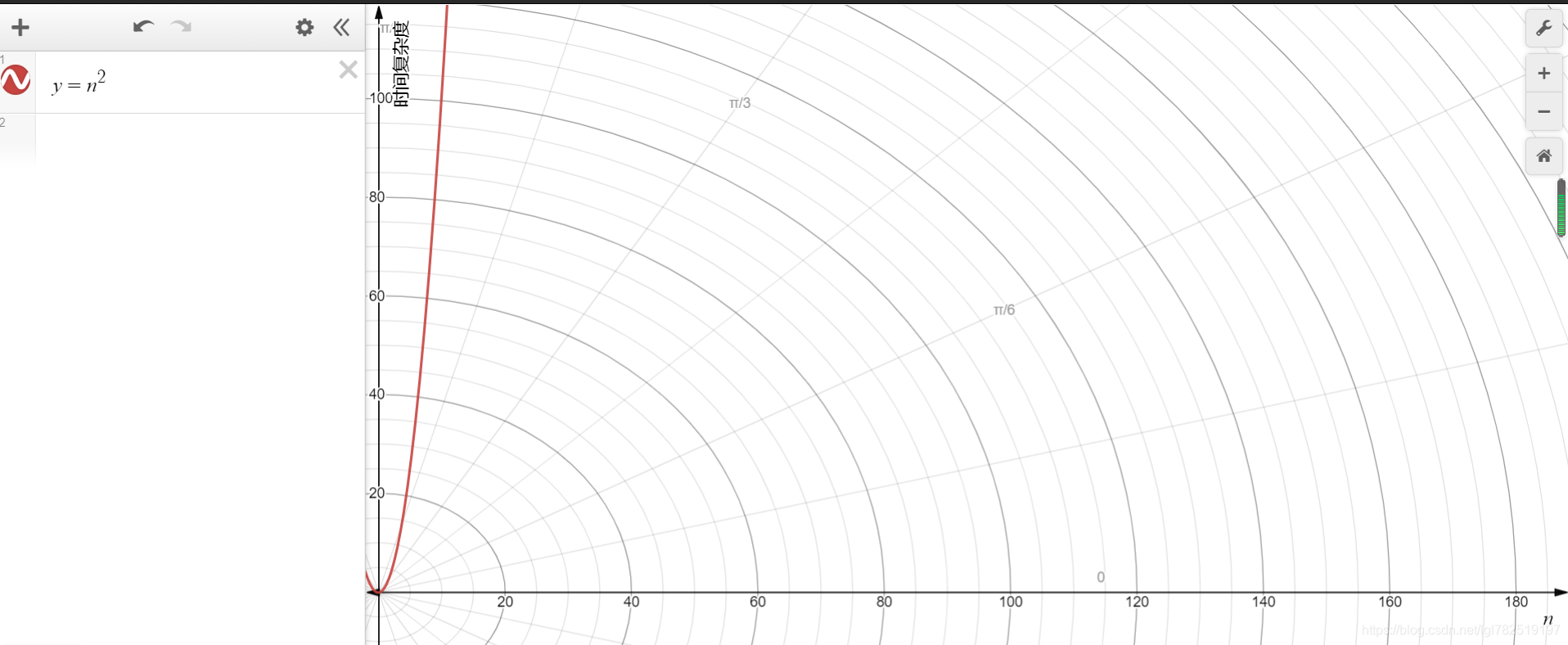
        所以T(n)=1+2+3+…+(n-3)+(n-2)+(n-1)，这是一个等差数列，根据等差数列的求和公式：
$$S_n=\frac{(a_1+a_n)n}{2}，n\in N^{\ast }$$
        所以$$T(n)=\frac{(1+n-1)(n-1)}{2}=\frac{1}{2}{n}^2-\frac{n}{2}$$

        按照推到大O阶的规则第2第3条，那么我们的时间复杂度为O(n²)，其图像走势为

4-4-对数阶-O(logⁿ)

例子1

int number=1;
while(number<n){
   
   
	// 执行一次
	number=number*2;
	//时间复杂度为O(1)的算法，算作是执行一次
	...
}

        我们分析一下：假设第m次进来的后，number >= n

        第1次进来，number=2¹=2<n，执行了1+1=2次
        第2次进来，number=2²=4<n，执行了1+1=2次
        第3次进来，number=2³=8<n，执行了1+1=2次
        …,…,…,…,…,…,…,
        第m-2次进来，number=2^m-2<n，执行了1+1=2次
        第m-1次进来，number=2^m-1<n，执行了1+1=2次
        第m次进来，number=2^m>=n，执行了1+1=2次
        第m+1次不满足条件，循环结束

        所以要结束循环，至少执行m次循环，执行了2m次，最次的情况是2^m=n，所以有$$T(n)=2m=2lo{g}_2^n=2lo{g}^n$$
        按照推到大O阶的规则第3条，那么我们的时间复杂度为:$$O(lo{g}^n)$$
        其图像走势为

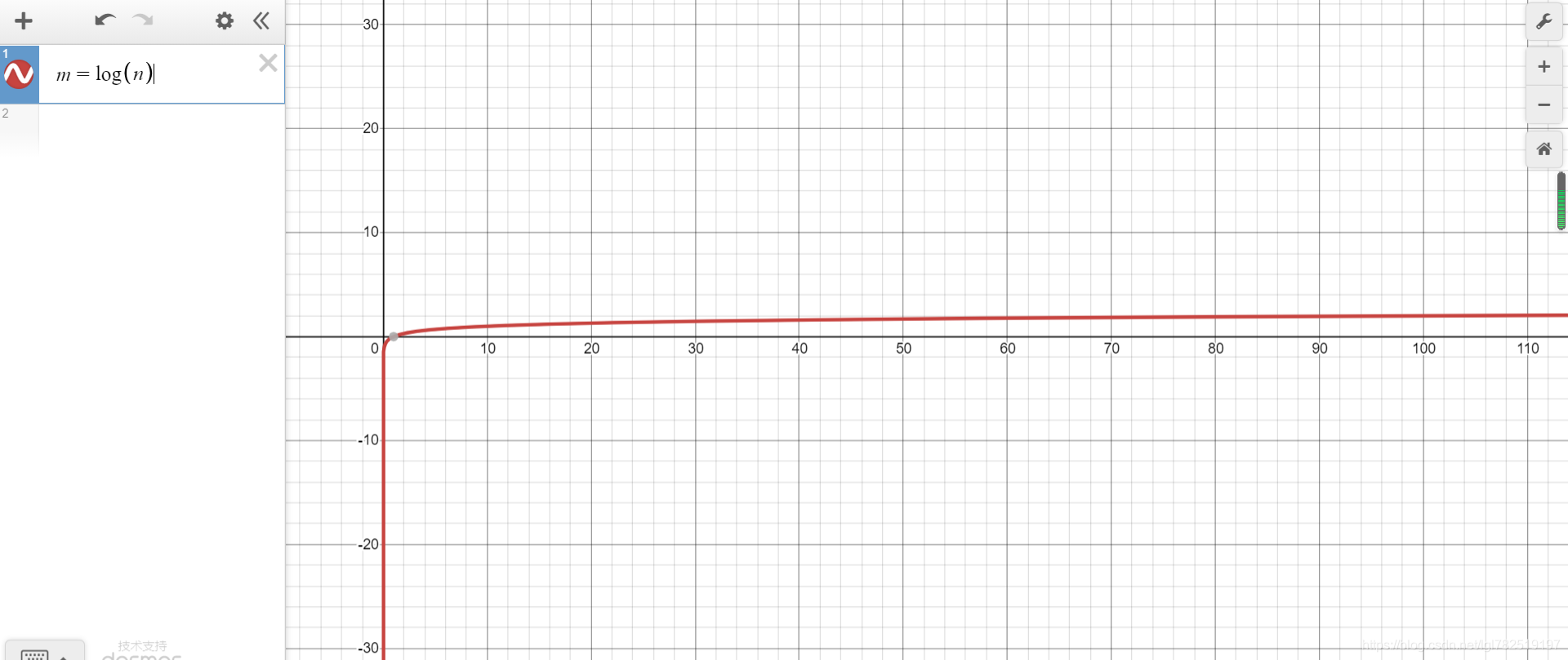
例子2，二分查找法

public static int binarySearch(int[] arr,int num){
   
   
	// 执行一次
    int end=arr.length-1;
    // 执行一次
    int begin = 0;
    // 执行一次
    int mid = 0;
    // 执行一次
    if(num < arr[begin] || num > arr[end] || begin > end){
   
   
        return -1;
    }