提供了堆栈实现法的函数、递归实现法的函数,并且还提供了完整的代码,在代码中有具体的代码注释
堆栈实现法:
有在代码中有具体的代码注释
def SeedFill(x, y):
# 图形空白点入栈
if point[x][y] == 0:
stack.append((x, y))
while len(stack) != 0:
# 栈顶像素出栈
seed = stack.pop()
x, y = seed
# 从种子点像右边填充
while point[x][y] == 0:
# 将已经被填充的点记作1
point[x][y] = 1
# 上色
plt.plot(x, y, 'r.', markersize=1)
plt.pause(0.01)
# 向右填充直到遇到边界
x = x + 1
# right为检查区间的最右像素
right = x - 1 # right需要减1,是因为上面的循环需要遇见边界点,但是right表示的是填充点的最右边的点
# 填充完右边的空白点之后,回到种子点,准备向种子点左右填充
x, y = seed
x = x - 1
# 向种子点左边填充
while point[x, y] == 0:
point[x][y] = 1
plt.plot(x, y, 'r.', markersize=1)
# 设置暂停,实现动画效果
plt.pause(0.01)
# 向种子点的左边填充
x = x - 1
# left为检查区间的最左像素
left = x + 1
# 将新的种子点入栈
# 处理上一条扫描线
x = left
y = y + 1
# 为了更好的选取种子点,所以引入flag参数(flag=True 说明是可以入栈的点)
while x < right:
# 初始化flag
flag = False
while point[x][y] == 0:
flag = True
x = x + 1
if flag:
stack.append((x - 1, y))
# 种子点入栈之后需要重新将flag重置为False,不然在循环里面flag就一直会是true的
flag = False
while point[x][y] != 0 and x < right:
# 使用这个语句,是为了防止图形有洞的情况,有洞,但是还是需要遍历到最右边
x = x + 1
# 处理下一条扫描线
x = left
y = y - 2 # 因为在前面的是先处理了上一条扫面线,所以需要-2
while x < right:
flag = False
while point[x][y] == 0:
flag = True
x = x + 1
if flag:
stack.append((x - 1, y))
flag = False
while point[x][y] != 0 and x < right:
x = x + 1递推式:
# 种子填充算法(递归式)
def seedFill(x, y):
if point[x][y] == 0:
point[x][y] = 1
plt.plot(x, y, 'r.', markersize=1)
plt.pause(0.1)
if point[x + 1][y] == 0:
seedFill(x + 1, y)
if point[x][y + 1] == 0:
seedFill(x, y + 1)
if point[x - 1][y] == 0:
seedFill(x - 1, y)
if point[x][y - 1] == 0:
seedFill(x, y - 1)使用DDA算法进行直线的绘制(多边形的边缘)
# DDA直线扫描算法,用于绘制多边形的边界
def DDA(x1, y1, x2, y2):
dx, dy = x2 - x1, y2 - y1
k = dy / dx
x, y = x1, y1
# 绘点
for i in range(0, int(abs(dx) + 1)):
# 网格线
plt.grid()
# x轴y轴数值取整
plt.gca().xaxis.set_major_locator(MaxNLocator(integer=True))
plt.gca().yaxis.set_major_locator(MaxNLocator(integer=True))
# 需要四舍五入
plt.plot(int(round(x)), int(round(y)), 'b.', markersize=1)
point[int(round(x))][int(round(y))] = 2
x += 1
y += float(k)完整代码
本代码还实现了种子填充的动画效果,如果不需要动画效果的,可以将 plt.pause(0.01) 代码删除,就没有动画效果了
# -*- coding=utf-8 -*-
# Author:lei吼吼
# @Time :2022/10/31 21:49
# @File: 种子填充.py
# @Software:PyCharm
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.ticker import MaxNLocator
np.set_printoptions(threshold=np.inf)
# 在矩阵point中,0表示空白点,1表示填充点,2表示边界点
# 初始化450*450的矩阵为零
point = np.zeros((450, 450))
stack = []
# 网格线
plt.grid(ls='--', which='major')
def SeedFill(x, y):
# 图形空白点入栈
if point[x][y] == 0:
stack.append((x, y))
while len(stack) != 0:
# 栈顶像素出栈
seed = stack.pop()
x, y = seed
# 从种子点像右边填充
while point[x][y] == 0:
# 将已经被填充的点记作1
point[x][y] = 1
# 上色
plt.plot(x, y, 'r.', markersize=1)
plt.pause(0.01)
# 向右填充直到遇到边界
x = x + 1
# right为检查区间的最右像素
right = x - 1 # right需要减1,是因为上面的循环需要遇见边界点,但是right表示的是填充点的最右边的点
# 填充完右边的空白点之后,回到种子点,准备向种子点左右填充
x, y = seed
x = x - 1
# 向种子点左边填充
while point[x, y] == 0:
point[x][y] = 1
plt.plot(x, y, 'r.', markersize=1)
# 设置暂停,实现动画效果
plt.pause(0.01)
# 向种子点的左边填充
x = x - 1
# left为检查区间的最左像素
left = x + 1
# 将新的种子点入栈
# 处理上一条扫描线
x = left
y = y + 1
# 为了更好的选取种子点,所以引入flag参数(flag=True 说明是可以入栈的点)
while x < right:
# 初始化flag
flag = False
while point[x][y] == 0:
flag = True
x = x + 1
if flag:
stack.append((x - 1, y))
# 种子点入栈之后需要重新将flag重置为False,不然在循环里面flag就一直会是true的
flag = False
while point[x][y] != 0 and x < right:
# 使用这个语句,是为了防止图形有洞的情况,有洞,但是还是需要遍历到最右边
x = x + 1
# 处理下一条扫描线
x = left
y = y - 2 # 因为在前面的是先处理了上一条扫面线,所以需要-2
while x < right:
flag = False
while point[x][y] == 0:
flag = True
x = x + 1
if flag:
stack.append((x - 1, y))
flag = False
while point[x][y] != 0 and x < right:
x = x + 1
# 种子填充算法(递归式)
def seedFill(x, y):
if point[x][y] == 0:
point[x][y] = 1
plt.plot(x, y, 'r.', markersize=1)
plt.pause(0.1)
if point[x + 1][y] == 0:
seedFill(x + 1, y)
if point[x][y + 1] == 0:
seedFill(x, y + 1)
if point[x - 1][y] == 0:
seedFill(x - 1, y)
if point[x][y - 1] == 0:
seedFill(x, y - 1)
# DDA直线扫描算法,用于绘制多边形的边界
def DDA(x1, y1, x2, y2):
dx, dy = x2 - x1, y2 - y1
k = dy / dx
x, y = x1, y1
# 绘点
for i in range(0, int(abs(dx) + 1)):
# 网格线
plt.grid()
# x轴y轴数值取整
plt.gca().xaxis.set_major_locator(MaxNLocator(integer=True))
plt.gca().yaxis.set_major_locator(MaxNLocator(integer=True))
# 需要四舍五入
plt.plot(int(round(x)), int(round(y)), 'b.', markersize=1)
point[int(round(x))][int(round(y))] = 2
x += 1
y += float(k)
# 绘制多边形的边
def draw(x, y, xEnd, yEnd):
if xEnd < x:
x, y, xEnd, yEnd = xEnd, yEnd, x, y
DDA(x, y, xEnd, yEnd)
# 绘制多边形
def drawLine():
draw(0, 40, 40, 18)
draw(40, 18, 80, 40)
draw(0, 40, 60, 60)
draw(60, 60, 80, 40)
draw(20, 40, 40, 48)
draw(40, 48, 50, 40)
draw(50, 40, 40, 30)
draw(40, 30, 20, 40)
# 网格线
plt.grid()
if __name__ == '__main__':
# 画出图形的边界
drawLine()
plt.grid()
# 选取(40,18)作为种子起始点
SeedFill(40, 28)
plt.show()
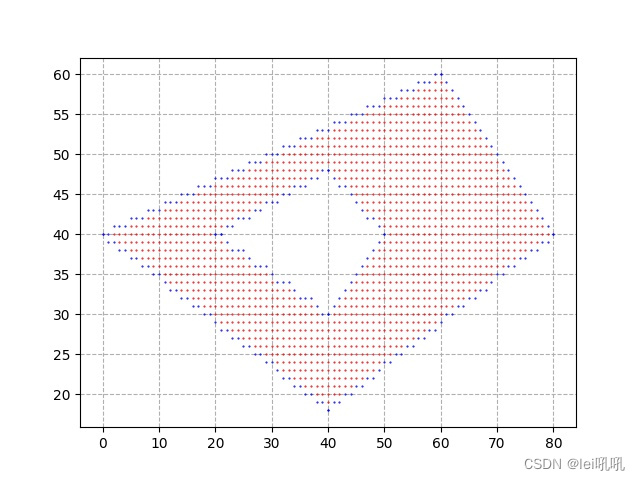
最终结果
























 3825
3825

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








