组合数学题目之编程实现

前言

之前学习《组合数学》时，对几个小题目进行了编程实现，现整理到这里。

题目1

实现组合$C_n^r$和排列$A_n^r$
解析：先构造一个求阶乘的方法factorial(n)，用递归方法实现。
然后构造求组合数方法combination(n, r)，求排列数的方法permutation(n, r)，根据组合和排列的定义，调用求阶乘的方法factorial(n)。
用Python编程实现：

def factorial(n):
    if n == 1:
        return n
    else:
        return n * factorial(n - 1)

def combination(n, r):
    first = factorial(n)
    print("%s的阶乘为: %s" % (n, first))
    second = factorial(r)
    print("%s的阶乘为: %s" % (r, second))
    third = factorial((n - r))
    print("%s的阶乘为: %s" % (n-r, third))
    return first / (second * third)

def permutation(n, r):
    return factorial(n)/factorial(n-r)

if __name__ == "__main__":
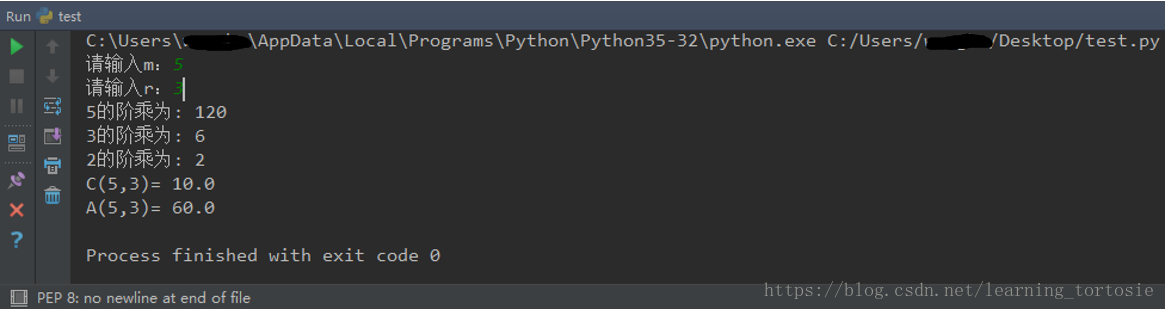
    m = int(input("请输入m："))
    r = int(input("请输入r："))
    result1 = combination(m, r)
    result2 = permutation(m, r)
    print("C(%s,%s)= %s" % (m, r, result1))
    print("A(%s,%s)= %s" % (m, r, result2))

运行结果为：

题目2

由26个英文字母构成长度为5的字符串，要求：
（1）6个母音a,e,i,o,u,y不相邻；
（2）其余20个子音不存在3个相邻；
（3）相邻的子音不相同；
求有多少这样的字符？设计程序实现。
用Python编程实现：

def sorting(n):
    y = ['a', 'b']
    for i in range(n-1):
        for x in y[:]:
            y.remove(x)
            if x[-1] == 'b':
                if len(x) >= 2:
                    if x[-2] == 'b':
                        x = x + 'a'
                        y.append(x)
                    else:
                        x1 = x + 'a'
                        x2 = x + 'b'
                        y.append(x1)
                        y.append(x2)
                else:
                    x1 = x + 'a'
                    x2 = x + 'b'
                    y.append(x1)
                    y.append(x2)
            else:
                x = x + 'b'
                y.append(x)
    return y

def deal(y):
    sum = 0
    for x in y:
        ca = x.count('a')
        cb = x.count('b')
        cbb = x.count('bb')
        if cbb != 0:
            sum += 6**ca*20**(cb-cbb)*19**cbb
        else:
            sum += 6**ca*20**cb
    return sum

if __name__ == "__main__":
    y = sorting(5)
    sum = deal(y)
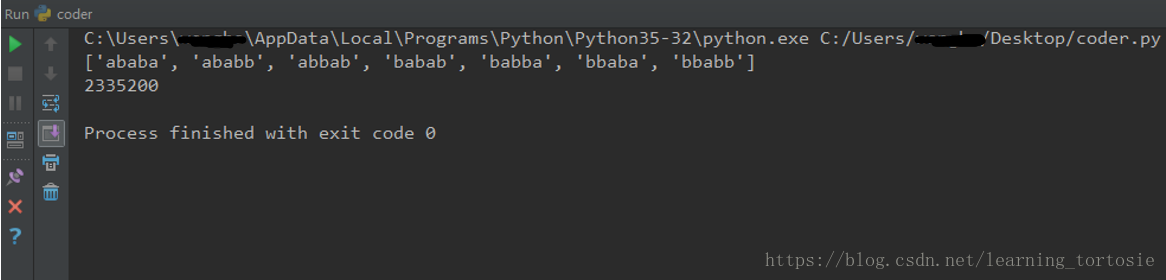
    print(y)
    print(sum)

运行结果为：

题目3

证明：$\bigl(\begin{smallmatrix} m+n \\ r \end{smallmatrix} \bigr)=\bigl(\begin{smallmatrix} m \\ 0 \end{smallmatrix} \bigr)\bigl(\begin{smallmatrix} n \\ r \end{smallmatrix} \bigr)+\bigl(\begin{smallmatrix} m \\ 1 \end{smallmatrix} \bigr)\bigl(\begin{smallmatrix} n \\ r-1 \end{smallmatrix} \bigr)+…+\bigl(\begin{smallmatrix} m \\ r \end{smallmatrix} \bigr)\bigl(\begin{smallmatrix} n \\ 0 \end{smallmatrix} \bigr), r≤min(m,n)$
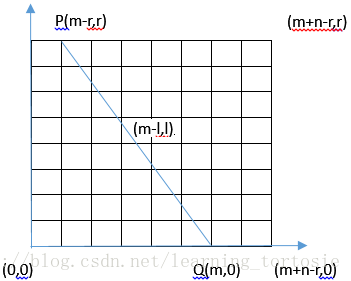
解析：如下图所示，P(m-r,r) ，Q(m,0)是图上两点，PQ上各网点坐标（m-l,l）,从(0,0)点到(m+n-r,r)的路径数应为C(m+n,r)，每条路径都必须通过PQ线上一点，设为(m-l,l)点。
从(0,0)点到(m-l,l)点的路径数为C(m,l)，从(m-l,l)点到(m+n-r,r) 点的路径数为C(n,r-l)。
根据乘法法则，从(0,0)点经(m-l,l)点到(m+n-r,r) 点的路径数为C(m,l)*C(n,r-l)。
又根据加法法则有：

$$\bigl(\begin{smallmatrix} m+n \\ r \end{smallmatrix} \bigr)=\bigl(\begin{smallmatrix} m \\ 0 \end{smallmatrix} \bigr)\bigl(\begin{smallmatrix} n \\ r \end{smallmatrix} \bigr)+\bigl(\begin{smallmatrix} m \\ 1 \end{smallmatrix} \bigr)\bigl(\begin{smallmatrix} n \\ r-1 \end{smallmatrix} \bigr)+…+\bigl(\begin{smallmatrix} m \\ r \end{smallmatrix} \bigr)\bigl(\begin{smallmatrix} n \\ 0 \end{smallmatrix} \bigr)$$

通过编程证明，分别编写计算等号两边数值的函数，然后给m,n,r赋值，比较结果。

import math

def combination(n, r):
    return math.factorial(n) / (math.factorial(r) * math.factorial((n - r)))

def test(m, n, r):
    sum = 0
    for i in range(r+1):
        a = combination(m, i)
        b = combination(n, r - i)
        sum += a * b
    return sum

if __name__ == "__main__":
    print('第一组验证数据')
    print(int(test(3, 2, 2)))  # m=3, n=2, r=2
    print(int(combination(5, 2)))
    print('第二组验证数据')
    print(int(test(9, 10, 8)))  # m=9, n=10, r=8
    print(int(combination(19, 8)))

如下图所示，分别随机取了两组数据，结果相同，可以证明等号两边相等。