五月训练 Day13

原创已于 2022-05-13 21:45:56 修改 · 247 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#链表 #数据结构

于 2022-05-13 20:20:13 首次发布

Leetcode 训练专栏收录该内容

22 篇文章

订阅专栏

文章目录

写在前面：
今天的习题进入了双链表部分，双链表的数据结构并不复杂，写算法时只要维护好节点间的指针关系即可，常用的技巧与单链表相差不大。

1. Leetcode 430. 扁平化多级双向链表

你会得到一个双链表，其中包含的节点有一个下一个指针、一个前一个指针和一个额外的子指针。这个子指针可能指向一个单独的双向链表，也包含这些特殊的节点。这些子列表可以有一个或多个自己的子列表，以此类推，以生成如下面的示例所示的多层数据结构。
给定链表的头节点 head ，将链表扁平化，以便所有节点都出现在单层双链表中。让 curr 是一个带有子列表的节点。子列表中的节点应该出现在扁平化列表中的 curr 之后和 curr.next 之前。
返回扁平列表的 head 。列表中的节点必须将其所有子指针设置为 null 。

分析与解答

本题使用迭代方法进行解答：

在搜索中，若当前节点包含子节点，则调用 flatten 函数展平双向链表，并返回展平后双向链表的头节点（当前节点的子节点）；
若不包含子节点，则将当前节点移向下一个，重复步骤 1，2

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* prev;
    Node* next;
    Node* child;
};
*/

class Solution {
public:
    Node* flatten(Node* head) {
        if (head == nullptr) { // 防止 head 为 nullptr 的情况
            return head;
        }
        
        Node* data(head); // 正在搜索的当前节点
        Node* flatHead(nullptr); // 展平后双向链表的头节点
        Node* nxtHead(nullptr); // 记录当前节点的下一个节点
        while (data != nullptr) {
            if (data->child) { // 当前节点有子节点，扁平化当前节点
                nxtHead = data->next; // 重新链接时会破坏链表关系，因此记录当前节点的下一个节点
                // 扁平化子节点并返回子节点的头
                flatHead = flatten(data->child);
                // 重新连接，data <-> flatHead <-> flatHeadEnd <-> nxtHead
                data->child = nullptr;
                data->next = flatHead; // data <-> flatHead
                flatHead->prev = data;
                // 找 flatHeadEnd，注意扁平化时已经链接 flatHead <-> flatHeadEnd
                while (flatHead->next) {
                    flatHead = flatHead->next;
                }
                flatHead->next = nxtHead; // 链接 flatHeadEnd <-> nxtHead
                if (nxtHead) { // 若 nxtHead 不为 nullptr，则将其前向节点设置为 flatHeadEnd
                    nxtHead->prev = flatHead;
                }
                data = nxtHead; // 移动当前节点到下一节点
            } else { // 当前节点无子节点，移向下一个节点
                data = data->next;
            }
        }
        
        return head;
    }
};

2. Leetcode 剑指 Offer II 028. 展平多级双向链表

多级双向链表中，除了指向下一个节点和前一个节点指针之外，它还有一个子链表指针，可能指向单独的双向链表。这些子列表也可能会有一个或多个自己的子项，依此类推，生成多级数据结构，如下面的示例所示。
给定位于列表第一级的头节点，请扁平化列表，即将这样的多级双向链表展平成普通的双向链表，使所有结点出现在单级双链表中。

分析与解答

送分题，与上一题相同 😃

3. Leetcode 剑指 Offer 36. 二叉搜索树与双向链表

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。

分析与解答

本题思路很简单，但是代码较难。先说思路，由于提供的是二叉搜索树，因此中序遍历即可得到排序好的结果。在遍历过程中按遍历顺序依次链接节点，即可在不创建任何新节点的情况下完成双向链表的建立。代码如下：

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* left;
    Node* right;

    Node() {}

    Node(int _val) {
        val = _val;
        left = NULL;
        right = NULL;
    }

    Node(int _val, Node* _left, Node* _right) {
        val = _val;
        left = _left;
        right = _right;
    }
};
*/
class Solution {
public:
	// 借助中序遍历的思想，在中序遍历过程中创建双向链表即可
	// 这里我们指定 left 为前向指针，right 为后向指针
    Node* treeToDoublyList(Node* root) {
        if (root == nullptr) { // 当节点为空时返回空指针
            return nullptr;
        }
        // 子节点返回由自己构成的循环链表
        if (root->left == nullptr && root->right == nullptr) {
            root->left = root;
            root->right = root;
            return root;
        }
        
        Node* head(nullptr); // 双向链表的头节点，指向链表中最小元素
        Node* rightTree = root->right; // 由于更新中间节点时会破坏指针，因此提前记录右子树
        Node* rightSorted(nullptr); // 右子树排序后的头节点
        if (root->left != nullptr) { // 左子树非空时创建左双向链表
            head = treeToDoublyList(root->left);
        }
        if (head == nullptr) { // 中间节点必不为空，若左子树为空，由中间节点创建头节点
            head = root;
            root->left = root;
            root->right = root;
        } else { // 左子树非空，在双向链表中插入中间节点
            Node* headPrev = head->left; // 双向链表的尾节点
            headPrev->right = root; // 在尾节点后插入中间节点作为新的尾节点
            root->left = headPrev;
            root->right = head; // 在新的尾节点（中间节点）后插入头节点
            head->left = root; // 更新头节点的前向节点
        }
        if (rightTree) {
            // 右子树非空，在双向链表中插入右子树构成的双向链表
            rightSorted = treeToDoublyList(rightTree);
            Node* headPrev = head->left;
            Node* rHeadPrev = rightSorted->left; // （1）记录右子树双向链表的尾节点
            headPrev->right = rightSorted; // 更新尾节点，插入右子树双向链表头节点
            rightSorted->left = headPrev;
            rHeadPrev->right = head; // （1）更新右子树双向链表的尾节点
            head->left = rHeadPrev;
        }
        
        return head;
    }
};

以下图的二叉搜索树为例，其双向链表建立过程如下，依照代码中的约定，图中指针 p 为 left，n 为 right：
一个栗子
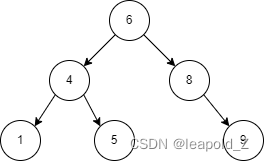
（1）中序遍历中第一个节点构造头节点：

（2）中序遍历中插入中间节点：
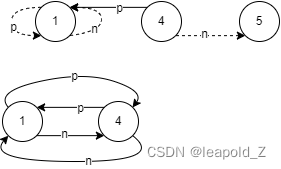
在这里插入图片描述
（3）中序遍历中插入右子树构造的双向链表：
右节点
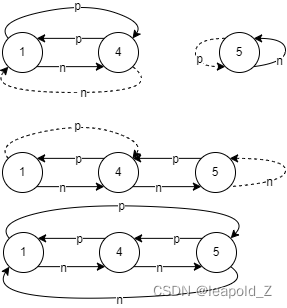
与步骤（2）相同，插入节点 6，此时使用节点 6 的右子树构造完双向链表，整体情况如下：

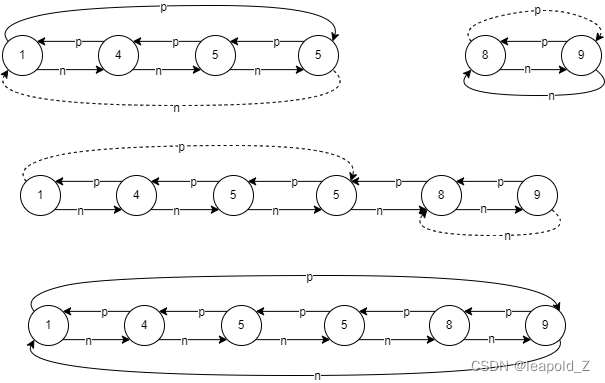
如此完成构造。