12月23-24日

01
前言
梯度下降法(Gradient Descent)是机器学习中最常用的优化方法之一,常用来求解目标函数的极值。
其基本原理非常简单:沿着目标函数梯度下降的方向搜索极小值(也可以沿着梯度上升的方向搜索极大值)。
但是如何调整搜索的步长(也叫学习率,Learning Rate)、如何加快收敛速度以及如何防止搜索时发生震荡却是一门值得深究的学问。
在上篇文章《梯度下降法快速教程 | 第一章:Python简易实现以及对学习率的探讨》中我们简单分析了学习率大小对搜索过程的影响,发现:
-
学习率较小时,收敛到极值的速度较慢。
-
学习率较大时,容易在搜索过程中发生震荡。
因此本篇文章中将简单讲解“冲量”的原理以及如何用“冲量”来解决上述两个问题。
全部源代码可在本人的GitHub:monitor1379中下载。
02
冲量:momentum
“冲量”这个概念源自于物理中的力学,表示力对时间的积累效应。
在普通的梯度下降法x += v中,每次x的更新量v为v = - dx * lr,其中dx为目标函数func(x)对x的一阶导数。
当使用冲量时,则把每次x的更新量v考虑为本次的梯度下降量- dx * lr与上次x的更新量v乘上一个介于[0, 1]的因子momentum的和,即v = - dx * lr + v * momemtum。
从公式上可看出:
-
当本次梯度下降- dx * lr的方向与上次更新量v的方向相同时,上次的更新量能够对本次的搜索起到一个正向加速的作用。
-
当本次梯度下降- dx * lr的方向与上次更新量v的方向相反时,上次的更新量能够对本次的搜索起到一个减速的作用。
使用冲量的梯度下降法的Python代码如下:
import numpy as npimport matplotlib.pyplot as plt# 目标函数:y=x^2def func(x): return np.square(x)# 目标函数一阶导数:dy/dx=2*xdef dfunc(x): return 2 * xdef GD_momentum(x_start, df, epochs, lr, momentum): """ 带有冲量的梯度下降法。 :param x_start: x的起始点 :param df: 目标函数的一阶导函数 :param epochs: 迭代周期 :param lr: 学习率 :param momentum: 冲量 :return: x在每次迭代后的位置(包括起始点),长度为epochs+1 """ xs = np.zeros(epochs+1) x = x_start xs[0] = x v = 0 for i in range(epochs): dx = df(x) # v表示x要改变的幅度 v = - dx * lr + momentum * v x += v xs[i+1] = x return xs
为了查看momentum大小对不同学习率的影响,此处设置学习率为lr = [0.01, 0.1, 0.6, 0.9],冲量依次为momentum = [0.0, 0.1, 0.5, 0.9],起始位置为x_start = -5,迭代周期为6。测试以及绘图代码如下:
def demo2_GD_momentum():
line_x = np.linspace(-5, 5, 100)
line_y = func(line_x)
plt.figure('Gradient Desent: Learning Rate, Momentum')
x_start = -5
epochs = 6
lr = [0.01, 0.1, 0.6, 0.9]
momentum = [0.0, 0.1, 0.5, 0.9]
color = ['k', 'r', 'g', 'y']
row = len(lr)
col = len(momentum)
size = np.ones(epochs+1) * 10
size[-1] = 70
for i in range(row):
for j in range(col):
x = GD_momentum(x_start, dfunc, epochs, lr=lr[i], momentum=momentum[j]) plt.subplot(row, col, i * col + j + 1)
plt.plot(line_x, line_y, c='b')
plt.plot(x, func(x), c=color[i], label='lr={}, mo={}'.format(lr[i], momentum[j]))
plt.scatter(x, func(x), c=color[i], s=size)
plt.legend(loc=0)
plt.show()
运行结果如下图所示,每一行的图的学习率lr一样,每一列的momentum一样,最左列为不使用momentum时的收敛情况:
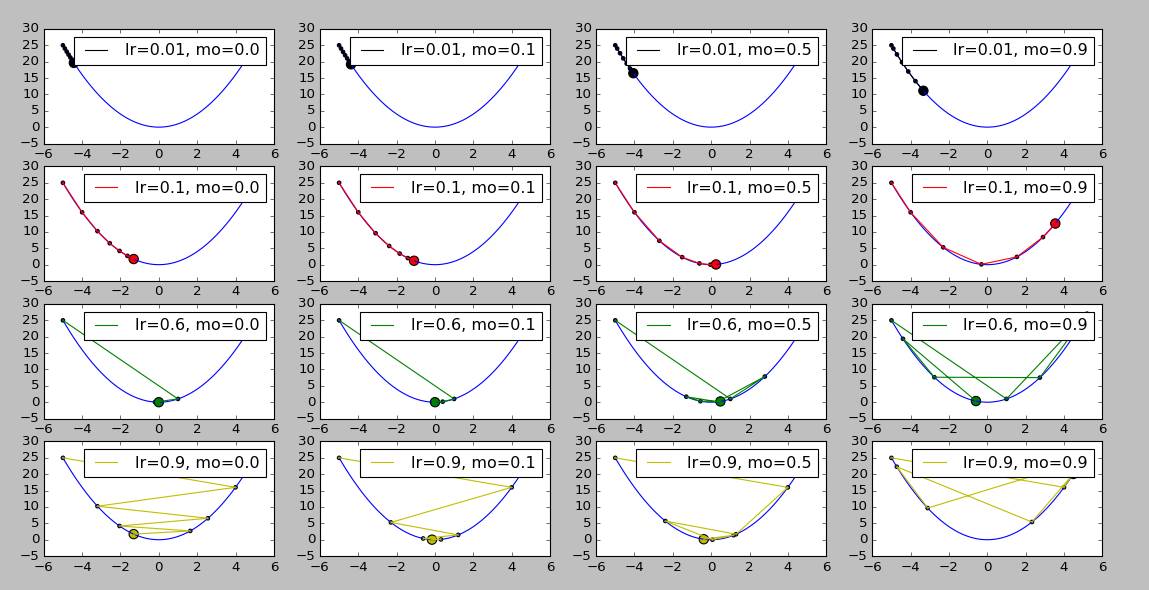
demo2_GD_momentum运行结果
简单分析一下运行结果:
-
从第一行可看出:在学习率较小的时候,适当的momentum能够起到一个加速收敛速度的作用。
-
从第四行可看出:在学习率较大的时候,适当的momentum能够起到一个减小收敛时震荡幅度的作用。
从上述两点来看,momentum确实能够解决在篇头提到的两个问题。
然而在第二行与第三行的最后一列图片中也发现了一个问题,当momentum较大时,原本能够正确收敛的时候却因为刹不住车跑过头了。那么怎么继续解决这个新出现的问题呢?下一篇文章《梯度下降法快速教程 | 第三章:学习率衰减因子(decay)的原理与Python实现》将介绍如何使用学习率衰减因子decay来让学习率随着迭代周期不断变小,让梯度下降法收敛时的“震荡”与“跑偏”进一步减少的方法。
原文链接:http://www.jianshu.com/p/58b3fe300ecb
查阅更为简洁方便的分类文章以及最新的课程、产品信息,请移步至全新呈现的“LeadAI学院官网”:
www.leadai.org
请关注人工智能LeadAI公众号,查看更多专业文章

大家都在看

TensorFlow从1到2 | 第三章 深度学习革命的开端:卷积神经网络

点击“阅读原文”直接打开报名链接




 本文介绍了梯度下降法中的冲量(momentum)原理,通过Python代码展示了如何使用冲量来调整搜索速度和防止震荡。实验结果显示,适当使用冲量能加速收敛并减小震荡,但过大可能导致过冲。下篇将讨论学习率衰减因子(decay)的应用。
本文介绍了梯度下降法中的冲量(momentum)原理,通过Python代码展示了如何使用冲量来调整搜索速度和防止震荡。实验结果显示,适当使用冲量能加速收敛并减小震荡,但过大可能导致过冲。下篇将讨论学习率衰减因子(decay)的应用。
















 2288
2288

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








