1.1 训练集 开发集 测试集
开发集(验证集):dev set 用来做交叉验证,检验不同的模型算法哪种最有效,最终我们的目的就是费尽全力改善模型在开发集上面的性能!
合理的调整这三个集合的比例,对模型整体至关重要。
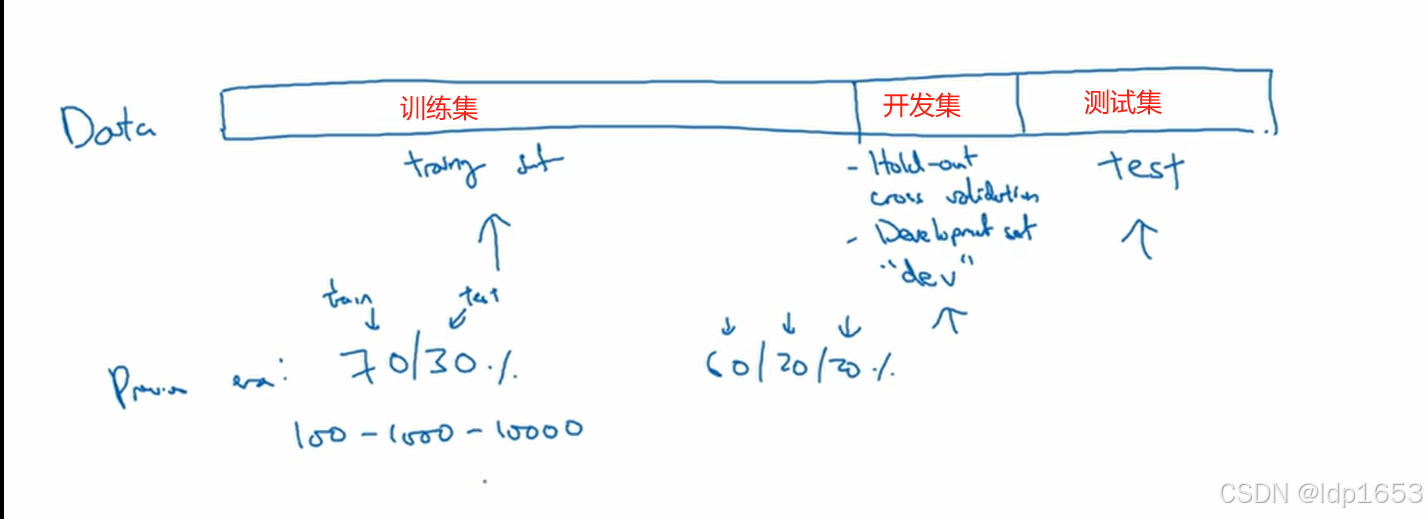
样本很小的时候,开发集和测试集可以各占20%
样本很大的时候 比如100w的数据集,开发集和测试集的比例可以降低到很低,比如各占1%
后续会讲解更详细的确定比例准则。
经验:用到大量爬虫数据的时候。确保开发集和测试集数据分布相同

1.2 偏差Bias 方差Variance
预备基础知识:
欠拟合过拟合:
【小萌五分钟】机器学习 | 鱼与熊掌 Tradeoffs: 前置小知识点之欠拟合(underfitting)&过拟合(overfitting)_哔哩哔哩_bilibili
偏差方差:
偏差: 预测值的数学期望与真实值之前的差值
方差:预测值和真实值的差值的平方和的和 除个5 就是方差。
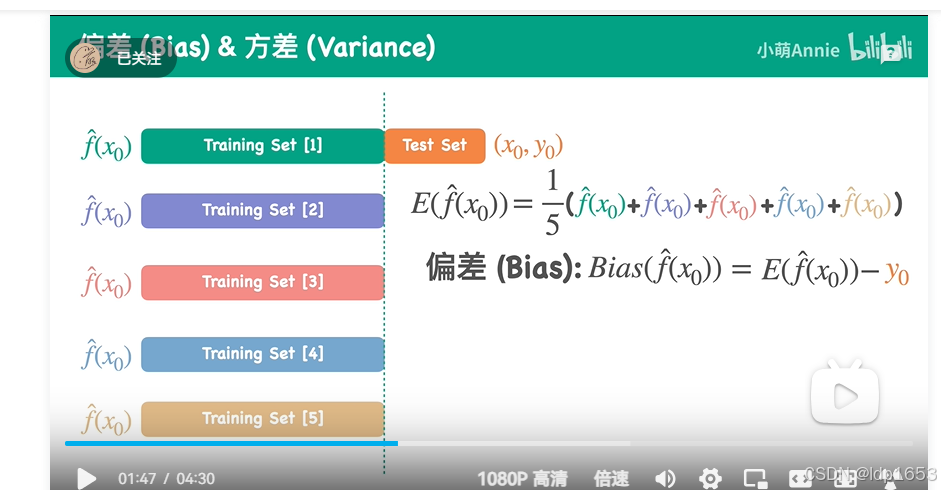
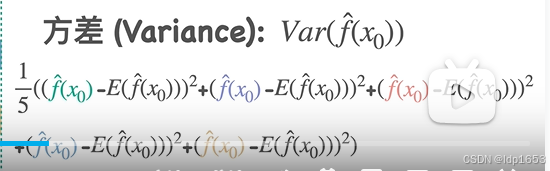

总结:
偏差:训练集可以看出算法是否拟合训练数据,总结出是否有偏差。
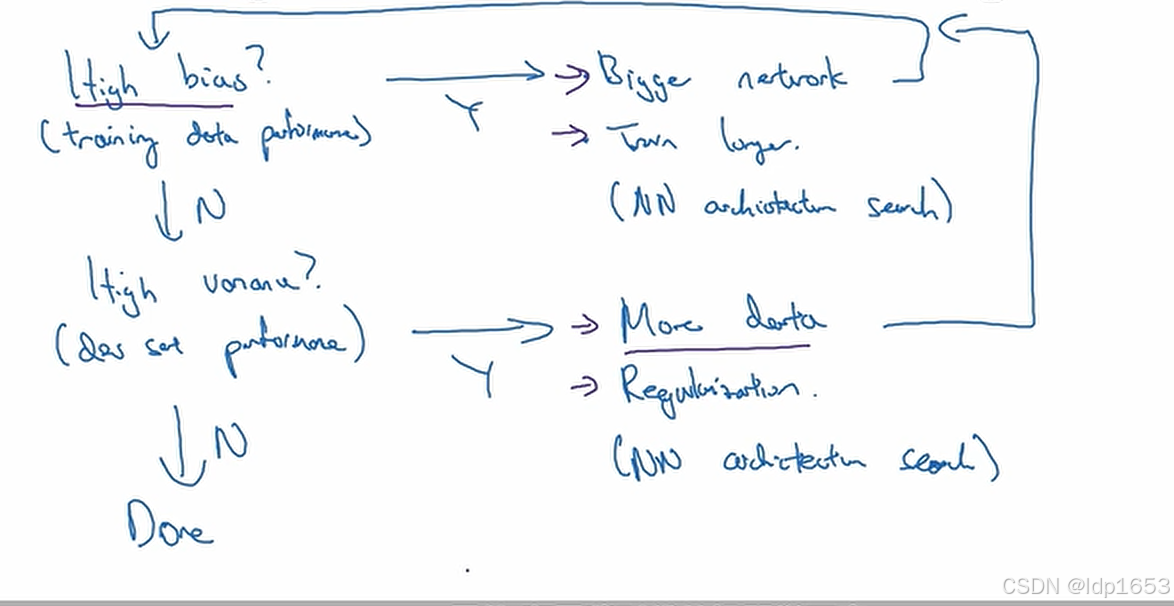
1.3 机器学习的基本配方
1.先看有没有高偏差 --看train set表现
有的话就换更大的网络(更多隐藏层更多隐藏单元)或者别的算法 或者训练时间更长
2.看看有无方差问题
有的话引入更多数据 或者正则(可以减少过拟合问题)
3.Done
1.4 正则化


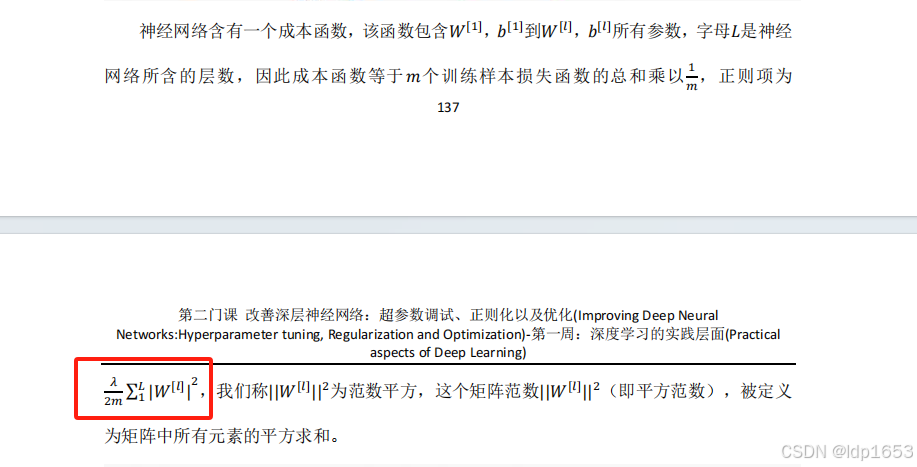



1.5 为什么正则化能防止过拟合
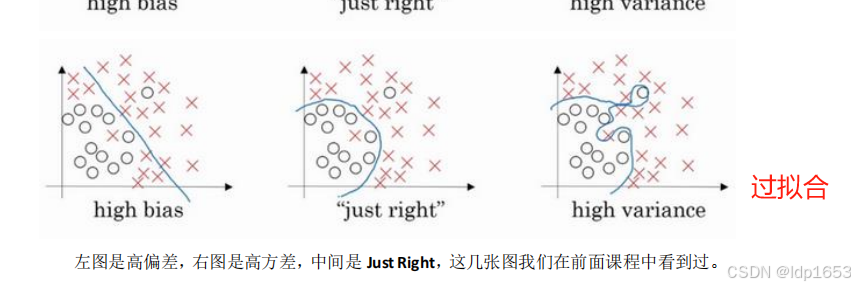
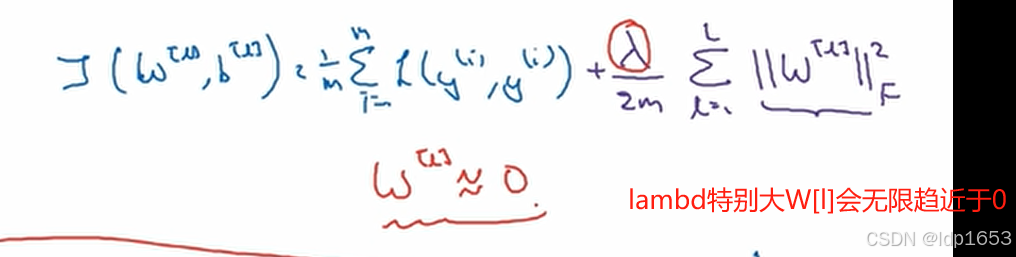
就会导致很多隐藏单元的影响变得微乎其微。
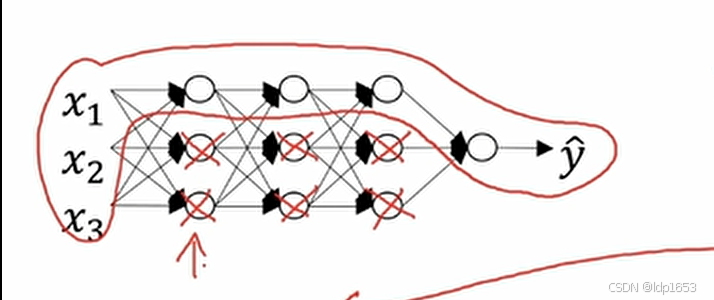
另一个例子:
tanh函数。


1.6 dropout正则化(随机失活)
之前介绍了L2正则,这里介绍另一种正则。
工作原理:
随机让节点失活,清除这些节点上的计算。这样我们实际上计算的就是一个小的多的神经网络。
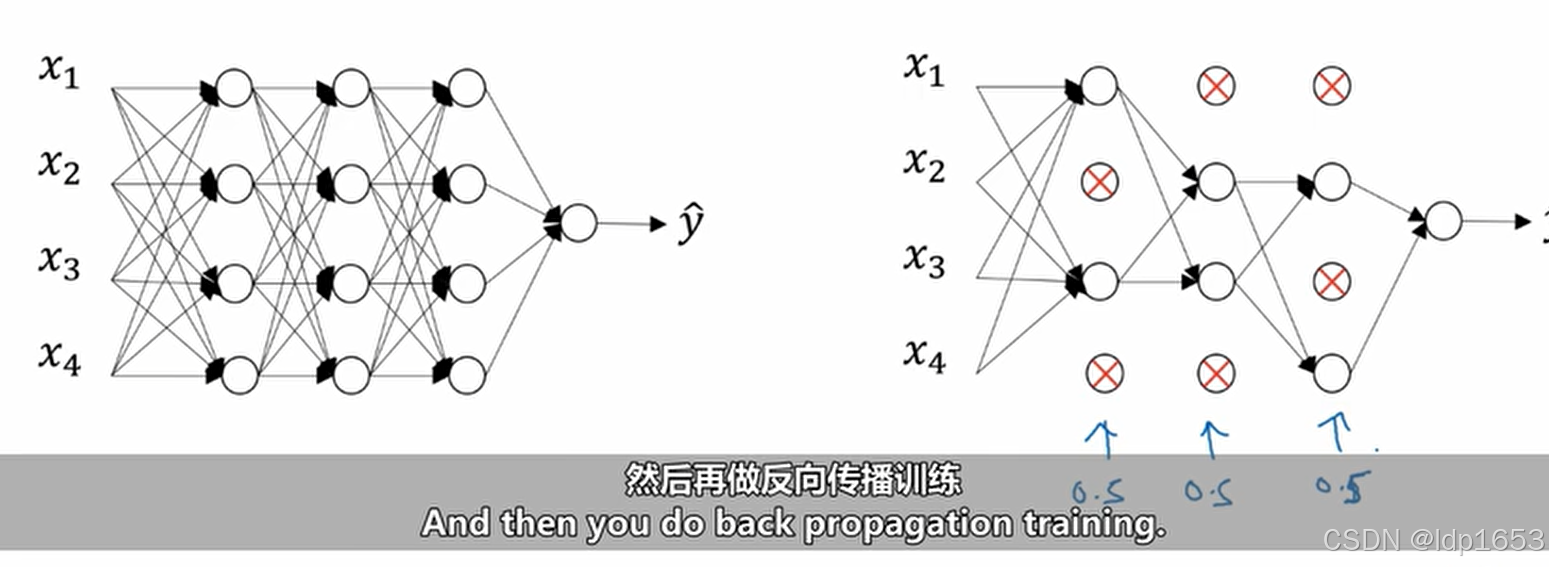
反向随机失活:

1.7 理解随机失活
意义就是:我用紫色圈起来的这个单元,它不能依靠任何特征,因为特征 都有可能被随机清除,或者说该单元的输入也都可能被随机清除。
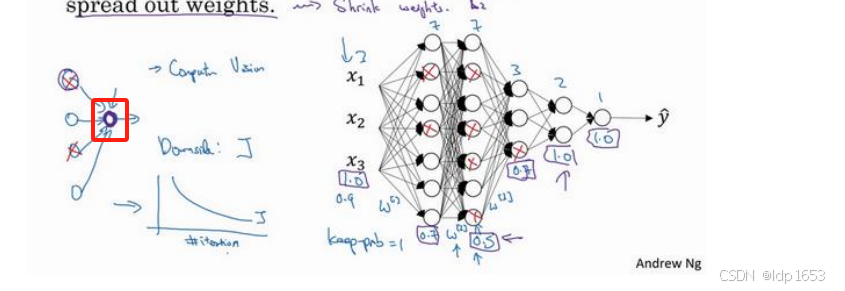
1.8 其他的正则化方法
早终止法
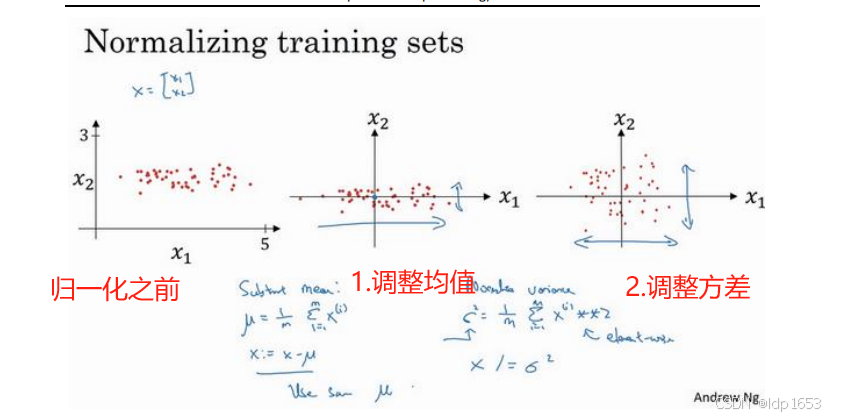
1.9 归一化输入
输入特征取值范围差异很大的时候需要用到归一化输入,如其中一个从 1 到 1000,另一个从 0 到 1,这对优化算法非常不利。使用归一化输入,可以大大加速神经网络的计算。
归一化需要两个步骤:
1.零均值
1.10 梯度消失和爆炸
权重W在深层神经网络意义重大,会让激活函数a指数级爆炸增长或者指数级递减.

1.11 神经网络的权重初始化
通用初始化公式:

1.12 梯度的数值近似
梯度检验使用双侧差值:

1.13 梯度检查
损耗函数J 最终可以转换成相对于sita的函数。
dsita同理,dsita维度和sita相同。 dsita是代价函数J的梯度(斜率)

 针对sita的所有分量sitai都按照上图方法计算一遍,最后得到两个向量。
针对sita的所有分量sitai都按照上图方法计算一遍,最后得到两个向量。
 10-5需要仔细检查向量的每个分量。
10-5需要仔细检查向量的每个分量。
1.14 梯度检查实施须知
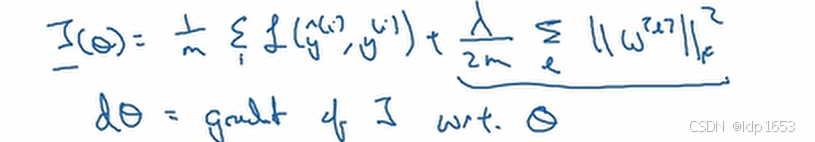





















 2480
2480

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








