密码学期中复习笔记

密码学期中复习笔记

Chapter 1 古典密码体制的Shannon理论

对称加密体制：

五元组$(P,C,K,E,D)$：明文空间，密文空间，密钥空间，加密变换，脱密变换

s.t. $\forall k,k\in K,x\in P,D(k,E(k,x))=x$(显然要求$d_k=D(k,\cdot )$为满射，$e_k=E(k,\cdot )$为单射)

几种经典的古典密码体制：

1. 移位密码：$P=C=K=Z_{26}$，$e_k(x)=x+k,d_k(x)=x-k$

2. 仿射密码：$P=C=Z_{26},K=Z_{26}^{\times }\times Z_{26}$，$e_k(x)=ax+b$，$d_k(x)=a^{-1}(y-b)$

3. 代换密码：$P=C=Z_{26},K=S_{26}$，$e_{\pi }(x)=\pi (x)$，$d_k(x)={\pi }^{-1}(x)$

​ 以上三种密码都是明文密文一对一的密码，因此若明文是文字的话，很容易使用文字的统计规律破译

4. Vignere密码：$P=C=K=Z_{26}^m$，$e_k(\vec{x})=\vec{x}+\vec{k},d_k(\vec{x})=\vec{x}-\vec{k}$

5. Hill密码：$P=C=Z_{26}^m$，$K=g{l}_m(Z_{26})$（$Z_{26}$上的m阶可逆矩阵集）

​ 以上两种密码对明文做m个一组的分组，故称为分组密码

密码的分析（破译）：

分类：

（均默认已知加密规则（Kerckhoff假设），在实践中加密规则也确是容易获取的）

1. 唯密文分析：仅有密文y
2. 已知明文分析：有明文串x和对应的密文串y
3. 选择明文分析：有加密机的访问权：可获得任意明文串x对应的密文串y
4. 选择密文分析：有解密机的访问权：可获得任意密文串y对应的明文串x

敌手的目标：确定正在使用的密钥是什么

由于古典密码很弱，因此下面均考虑在唯密文分析的条件下进行密码破译

eg1：对仿射/代换密码的密码分析：使用英文单个字母/相邻单词的统计规律进行分析

eg2：对Vignere密码的密码分析：重合指数法

思想：提取恰当m时英文文本串的统计规律：

定义一个含有n个字符的字符串x的重合指数$I_C(x)$为x中两个随机元素相同的概率

英文文本的重合指数根据统计为0.065；随机生成的文本的重合指数则为0.038，因此：

若将Vignere密码的密文从左到右，从上到下排布至m列，则当m与分组的组数重合时，每一列都是若干英文文本的平移，从而重合指数应该和英文文本接近；否则则近似于随机文本。这样可以通过枚举的方式破解出m值。

进一步，通过互重合指数可以求出每组文本的平移量：对于给定的英文平移文本x,y，其互重合指数定义为${\sum }_i{x}_i{y}_{i+k}/nm$，其中$x_i$为字母i的出现次数，则当且仅当k等于y的平移量和x的平移量之差时，互重合指数接近0.065.

Shannon信息论与完善保密

对于离散加密，如果引入概率，则可以将其视为离散随机变量X到Y的一个映射。那么，据此可以定义完善保密性，$\forall x\in P,\forall y\in C,P(x|y)=P(x)$（知道密文对于了解明文完全没有用）

定理：移位密码当且仅当密钥在$Z_{26}$中等概率取值时完善保密

推广：一次一密加密体制：$P=C=K=(Z_2{)}^n,e_k(x)=k+x,d_k(y)=y+k$，保证了完善保密（在唯密文分析下不可能破译），但是密钥和明文必须等长，不可复用，效率很低。

引入：Shannon信息熵：$-{\sum }_i{p}_i\log p_i$

定理：$H(K|C)=H(P)+H(K)-H(C)$

（自然语言的）伪密钥分析

在对自然语言进行加密和解密时，可能对于同一个密文存在多个有意义的对应明文，例如river和arena的距离为3。我们希望推导伪密钥的期望个数下界。

定义自然语言熵为$H_L={\lim }_{n\to \infty }\frac{H(P^n)}{n}$（长度为n的语言串的熵平均值）

语言L的冗余度定义为$R_L=1-\frac{H_L}{\log |P|}$，例如英语的冗余度为0.75

定理：语言L的伪密钥期望个数下界为$\overline{s_n}\ge \frac{|K|}{|P{|}^{n{R}_L}}-1$

定义：唯一解距离：伪密钥期望下界数恰好等于0时n的值，对英文的代换密码来说则为25

安全性的分类：

计算安全性（计算用时++），可证明安全性（归约到计算复杂问题上），无条件安全性（不可能破译）

Chapter2 分组密码与高级加密标准（AES）

分组算法的结构：

K为一给定长度的二元密钥，以某种固定公开算法生成Nr个轮密钥$(K_1,...,K_{Nr})$，轮函数g以轮密钥和当前状态作为输入：即：

$w_0\leftarrow x,w_1\leftarrow g(w_0,K_1),...,w_{Nr}\leftarrow g(w_{Nr-1},K_{Nr}),y\leftarrow w_{Nr}$

为了解密，要求轮函数必须为单射，即存在$g^{-1}$：$g^{-1}(g(w,y),y)=w$

解密过程：$w_{Nr}\leftarrow y,w_{Nr-1}\leftarrow g^{-1}(w_{Nr},K_{Nr}),...,w_0\leftarrow g^{-1}(w_1,K_1),x\leftarrow w_0$

分组算法：代换-置换网络（SPN）

$l,m\in Z^{+}$，明文和密文为长为$lm$的二元向量。一个SPN的基本构成为两个置换：πS:{0,1}l\pi_S:\{0,1\}^lπS​:{0,1}l上的置换（S盒），πP:{1,...,lm}\pi_P:\{1,...,lm\}πP​:{1,...,lm}上的置换

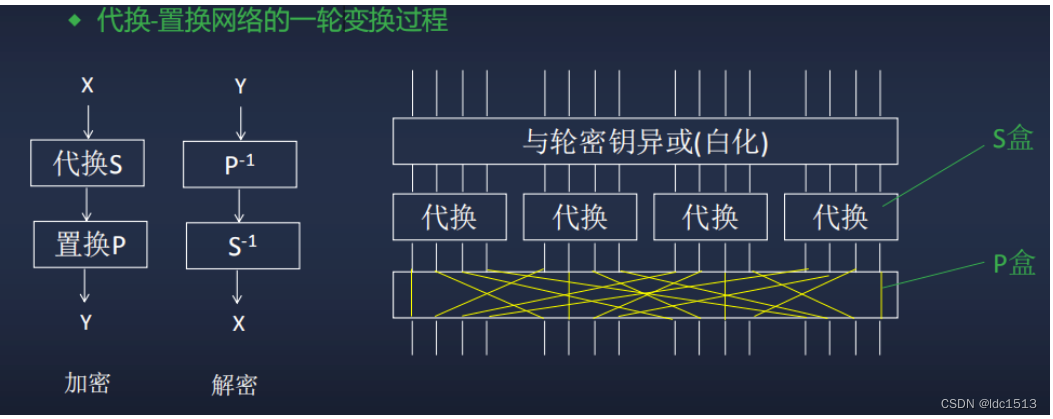
如上图所示，SPN加密的一轮会经过三层：第一层是和轮密钥的异或，第二层是对字符串切片为m段，分别用S盒代换，最后一层是对各个数字的所在位置用P盒代换；解密则反过来做即可。

SPN的伪代码为：

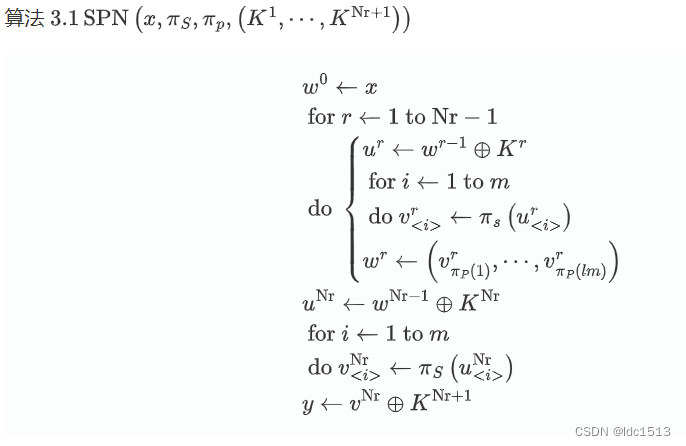
注：在最后两轮中没有再用${\pi }_P$，这是因为前面已经足够了

优点：该算法的实现非常简单高效，而且需要的存储空间较少

对SPN的分析

思想：在密文的输入中找到一些概率关系

1. 线性密码分析

分析方法：已知明文分析：给出大量明密对

SPN为线性密码，从而有性质：$SPN(u)=l(u)+A_0$，$l(u)=\prod (a_i^1{x}_1\oplus ...\oplus a_i^n{x}_n)$

定义：一个0/1随机变量的偏差：$ϵ=p(x=0)-\frac{1}{2}$

堆积引理：若$X_1,X_2,...,X_n$的偏差为${ϵ}_1,...,{ϵ}_n$，则$X_1\oplus ...\oplus X_n$的偏差为$2^{k-1}{\prod }_{j=1}^k{ϵ}_{i_j}$

攻击方法：

1. 对S盒${\pi }_S$构造线性逼近表：求出$\forall a=(a_1,...,a_l),b=(b_1,...,b_l)$，$\forall x_1,..,x_l,y_1,...,y_l={\pi }_s(x_1,..,x_l)$中$(a_1{x}_1\oplus ...\oplus a_l{x}_l)\oplus (b_1{y}_1\oplus ...\oplus b_l{y}_l)$的$N_L(a,b)$表（代表所有x1,…,xl中使得结果为0的个数），从而对每个S盒可以取特定的$a,b$，使得偏差偏离0
2. 在代换-置换网络中每一层都寻找恰当的$a,b$，使得构成一个相互抵消的活动S-盒的路径，并且偏差不大。
3. 假设这些路径变量相互独立，则其直和的偏差用堆积引理可以求出（记为$ϵ$）。而这些直和由于相互抵消的关系，最后自变量仅涉及到第一层和最后一层的若干变量。
4. 枚举最后一层变量对应的密钥，统计该直和对应的偏差，则在正确的密钥下，该直和应具有偏差$ϵ$，而其他密钥下偏差应为0
5. 为了区分正确的密钥和其它密钥，根据大数定律，需要统计的明密对数量应接近$c{ϵ}^{-2}$

2. 差分密码分析

分析方法：选择明文分析：可以获得任意明文对应的密文（比线性密码分析要求更高）

对任意的S盒πS:{0,1}m→{0,1}n\pi_S:\{0,1\}^m\rightarrow \{0,1\}^nπS​:{0,1}m→{0,1}n

定义：Δ(x′)={(x,x⊕x′)}\Delta (x')=\{(x,x\oplus x')\}Δ(x′)={(x,x⊕x′)}，即：输入异或为$x^{\prime }$的任意对；定义其输出异或为${\pi }_S(x)\oplus {\pi }_S(x\oplus x^{\prime })$

则：一共$2^m$个可能的输出异或分布在$2^n$个值上。同样的，可以对输出异或的分布建立列表：用$N_D(x,y)$表示输入异或为x，输出异或为y的对数，对$x,y$的所有可能取值，构造差分分布表

注意到，在SPN中，异或对同时异或一个密钥并不会对其异或产生影响，因此和线性密码分析一样，可以通过构造若干假设独立的差分链来得到差分链的一个扩散率$r$，从而同理可以通过枚举密钥的形式来分辨出正确的密钥（扩散率为$r$，即输入为链输入时，输出为链输出的概率为$r$），而其余密钥的概率接近0

加速算法：过滤：预先筛除一些不满足x,y条件的对。在剩下的里面再计数。

DES简介（1973-1996）

每个状态$u^i$被分为相同长度的两部分$L^i,R^i$，轮函数g：$g(L^{i-1},R^{i-1},K^i)=(L^i,R^i)$

其中，$L^i=R^{i-1},R^i=L^{i-1}\oplus f(R^{i-1},K)$

特性：这样的函数一定可逆：$g(R^i,L^i,K^i)=g(R^{i-1},L^{i-1})$

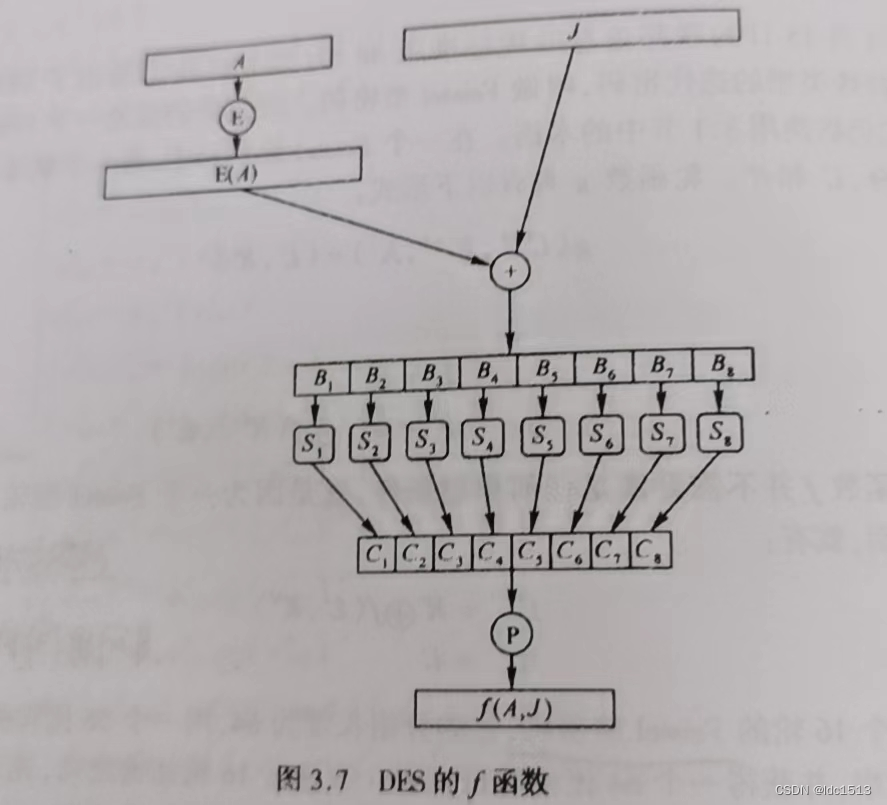
E：扩展函数；S_1,…,S_8：S盒（6bit$\to$ 4bit）；P：置换

分析：除了S盒以外均为线性部件，因此S盒的选取至关重要。但是S盒中也可能藏有“陷门”。

AES简介（1997-今）

数学基础：Galois Field $GF(2^8)$上的运算：$GF(2^8)\sim F_2[x]/m(x)=x^8+x^4+x^3+x^2+1$

$GF(2^8)$中恰有$2^8$个元素，且按照多项式各位的系数可以表示为$b_7{x}^7+...+b_0$，构成一个8元组$(b_7,...b_0)$，并且按照多项式运算任意非零元素都有逆

AES：三种可选密钥长度128,192,256, Nr分别为10,12,14

伪代码：

SubBytes：对于state中的每个字节（8个bite）先求$GF(2^8)$中的逆元素$(x_7,...,x_0)$，再做mod2乘法：

Shiftrows：行移位：将状态矩阵的第i行向左移动i位

MixColumns：列混合：对每一列做$GF(2^8)$上的乘法：原来的列为$(t_0,t_1,t_2,t_3{)}^T$，则得到的新列：
$$\begin{gathered} u_0=x\ast t_0+(x+1)\ast t_1+t_2+t_3 \\ {u}_1=x\ast t_1+(x+1)\ast t_2+t_3+t_0 \\ {u}_2=x\ast t_2+(x+1)\ast t_3+t_0+t_1 \\ {u}_1=x\ast t_3+(x+1)\ast t_0+t_1+t_2 \end{gathered}$$
KeyExpansion：将128bit的种子密钥变为11个轮密钥

AddRoundKey：$\text{state}\oplus K^r$

AES的分析：从设计上是反攻击的，例如有限域取逆的操作使得线性逼近和差分攻击趋于均匀分布，使得这两种攻击很难奏效。Mixcolumn的设计则使得找到包含较少S盒的攻击是不可能的。

Chapter3 序列密码

反馈移位寄存器序列：在GF(2)上，输入$a_0,...,a_{n-1}$，取函数$a_{n+i}=f(a_{n+i-1},...,a_{i-1})i=1,2,...$，则称序列{an}\{a_n\}{an​}为以f为反馈多项式的反馈移位寄存器序列。

定理：任意一个$GF(2^n)\to Gf(2)$的函数均可用多项式表示

序列密码：序列密码是一个七元组 $(\mathcal{X},\mathcal{Y},\mathcal{K},\mathcal{S},\tau ,e,d)$ 。其中 $\mathcal{X}、\mathcal{Y}、\mathcal{K}$ 和$\mathcal{S}$ 均为有限集合分别称为明文空间、密文空间、密钥空间和状态集。 $\tau$ 是带参数的状态转移函数, 即对于任意的 $k\in \mathcal{K}$,${\tau }_k:\mathcal{X}\times \mathcal{S}\to \mathcal{S};$$e$ 是带参数的加密函数, 即对于任意的 $k\in \mathcal{K}$，$e_k:\mathcal{X}\times \mathcal{S}\to \mathcal{Y};$ $d$ 是带参数的脱密函数, 即对于任意的 $k\in \mathcal{K}$，$d_k:\mathcal{Y}\times \mathcal{S}\to \mathcal{X}，$满足 $d_k\left(e_k\left(x_i,s_{i-1}\right),s_{i-1}\right)=x_i,1\le i\le n$.

加密：$y_i=e_k(x_i,s_{i-1}),s_i={\tau }_k(x_i,s_{i-1})$ 脱密：$x_i=d_k(x_i,s_{i-1}),s_i={\tau }_k(x_i,s_{i-1})$

在实际使用中，$s_i={\tau }_k(s_{i-1})$，$y_i=x_i\oplus \sigma (s_{i-1})$，称为伪随机数生成器

线性反馈移位寄存器：(LFSR)

$a_{n+i}=F\left(a_{i+n-1}{a}_{i+n-2}\cdots a_{i+1}{a}_i\right)=c_1{a}_{i+n-1}+c_2{a}_{i+n-2}+\cdots c_{n-1}{a}_{i+1}+c_n{a}_i$

其联结多项式为：$f(x)=1+c_{1}x+\cdots +c_{n-1}{x}^{n-1}+c_n{x}^n$；

特征多项式为：$\bar{f}(x)=x^n+c_1{x}^{n-1}+\cdots +c_{n-1}x+c_n$

记忆方法：特征多项式就是平时求数列的通项公式时使用的多项式，联结多项式就是它反过来；或者联结多项式可以看做是逆向递推式的参数：$a_0=a_n+c_1{a}_{n-1}+...+c_n{a}_1$，如果非退化

若$c_n\ne 0$，则称为非退化的。我们只研究非退化的情形。

注：显然，LFSR是终归周期的，非退化LFSR是周期的（参考下面的定理）

定理：对于一个多项式 $f(x)=1+c_{1}x+\cdots +c_{n-1}{x}^{n-1}+c_n{x}^n$ 和一个 半无限序列 $\alpha =a_0{a}_1{a}_2\cdots ,\alpha$ 是以 $f(x)$ 为联结多项式的 LFSR 序列的充分必要条件是形式幂级数 $\alpha (x)={\sum }_{i=0}^{\infty }{a}_i{x}^i$ 满足 $f(x)\cdot \alpha (x)$ 是多项式, $\mathrm{deg}[f(x)\cdot \alpha (x)]<n$; 而此时 $\alpha (x)$ 是周期的 当且仅当 $\mathrm{deg}[f(x)\cdot \alpha (x)]<\mathrm{deg}f(x)$.

特别地，若$c_n=1$，则$\mathrm{deg}f(x)=n>deg[f(x)\alpha (x)]$

对给定的序列 $\alpha =a_0{a}_1{a}_2\cdots$, 把满足 $f(x)\cdot \alpha (x)\in F_2[x]$ 的多项式的集合记为 $J(\alpha )$

则：$J(\alpha )$ 是 $F_2[x]$ 的理想

定义：极小多项式
称生成 $J(\alpha )$ 的多项式为极小多项式，记为 $m_{\alpha }(x)$. 显然当 $m_{\alpha }(x)\ne 0$ 时, $m_{\alpha }(0)=1$.
对满足 $g(0)=1$ 的 $g(x)\in F_2[x]$, 称使得 $g(x)\mid 1+x^L$ 的最小正整数 $\mathrm{L}$ 为 $g(x)$ 的周期, 记为 $p(g)$.

定理：若 $\alpha$ 是周期序列, 则 $p(\alpha )$（$\alpha$的周期）$=p\left(m_{\alpha }(x)\right)$.

定理：如果 $f(x)\in F_2[x]$ 是不可约的, 且 $f(0)=1,\alpha \ne 0$ 为以 $f(x)$ 为联结多项式的任一输出周期序列, 则 $m_{\alpha }(x)=f(x)$, 从而 $p(\alpha )=p(f(x)).$

定理：如果 $f(x)\in F_2[x]$ 是 $n$ 级LFSR 的联结多项式，用 $G(f)$ 表示由此多项式产生的全部序列。则 $G(f)$ 有一个是周期为 $2^n-1$ 的序列当且仅当 $f(x)$ 是一个次数为 $n$ 的本原多项式。（定义：$f(0)=1,f$不可约，$p(f)=2^n-1$）

意义：用一个很短的序列生成一个极长序列，加密一段极长密文。

定义：由n次本原多项式生成的序列称为n级的m-序列，下面证明$m-$序列的一些良好性质

m-序列统计特征：

定义：如果 $\alpha =a_0{a}_1\cdots$ 是 $F_2$ 上的周期为 $p(\alpha )$ 的周期序列, 称
$$C_{\alpha }(\tau )=\frac{1}{p(\alpha )}{\Sigma }_{k=0}^{p(\alpha )-1}(-1{)}^{a_k+a_{k+\tau }},(0\le \tau \le p(a)-1).$$
为 $\alpha$ 的自相关函数.

定理：设 $\alpha$ 是如果 $F_2$ 上是的 $n$ 级 $m$-序列, 则：

(1) $\alpha$ 的一个周期中 1 出现的个数是 $2^{n-1},0$ 出现的个数是 $2^{n-1}-1$.

(2)定义一个长为k的0-游程为10…0（k个）1；则：

0-游程和1-游程个数均为 $N/2=2^{n-2}$, 游程分布如下:

​ 长度为$i$的0 -游程 $N/2^{i+1},1\le i\le n-2$;

​ 长度为$i$的1-游程 $N/2^{i+1},1\le i\le n-2$;

​ 长度为n-1的0-游程1个;

​ 长度为n的1-游程1个

(3) $\alpha$ 的自相关函数是二值的:
$$C_{\alpha }(\tau )=\{\begin{array}{ll}1,& \text{ 当 }\tau =0;\\ -\frac{1}{p(\alpha )},& \text{ 当 }0<\tau \le p(\alpha )-1.\end{array}$$
从而：$\alpha$的自相关程度是极低的（$p(\alpha )=2^n-1$）

B-M算法与线性复杂度

给定一个序列 $\alpha =a_0{a}_1\cdots a_n$, 希望求出一个级数为 $I$ 的线性移位寄存器, 使得 $\alpha$ 可以由其生成, 且这样的 $I$ 最小。称 $I$ 为 $\alpha$的线性复杂度。

一致性定理：如果次数分别为 $L$ 和 $L^{\prime }$ 的两个联结多项式均可生成序列 $\alpha =a_0{a}_1\cdots a_{r-1}$, 并且 $r\ge L+L^{\prime }$, 则它们其后生成的序列相一致。

Massey 定理：如果序列 ${\alpha }_1=a_0{a}_1\cdots a_{r-2}$ 的线性复杂度是 $L$, 且产生 ${\alpha }_1$ 的 $L$ 级移位寄存器均不能产生 ${\alpha }_2=a_0{a}_1\cdots a_{r-2}{a}_{r-1}$, 则 ${\alpha }_2$ 的线性复杂度至少是 $r-L$ 。

B-M算法：给定一个序列片段 $\alpha =a_0{a}_1\cdots a_{N-1}$, 求一个多项式多项式 $f(x)$ 和级数$I$, 使得它可由以 $f(x)$ 为联结多项式的$I$级LFSR生成

Berlekamp-Massey 算法
输入: $\alpha =a_0{a}_1\cdots a_{N-1}$ ；
1: $n\leftarrow 0,\left(f_0(x),l_0\right)=(1,0)$;
2: 计算 $d_n=a_n-a_{n-1}{c}_1-\cdots -a_{n-l_n}{c}_{l_n}$;
(1) 若 $d_n=0$,
$\left(f_{n+1}(x),I_{n+1}\right)\leftarrow \left(f_n(x),I_n\right)$, 转步骤 3 ;
(2) 若 $d_n=1$ 且 $l_0=I_1=\cdots =I_n=0$,
$\left(f_{n+1}(x),I_{n+1}\right)\leftarrow \left(1+x^n,n+1\right)$, 转步骤 3 ;
(3) 若 $d_n=1$ 且 $I_m<I_{m+1}=I_{m+2}=\cdots =I_n(m<n)$,
(fn+1(x),In+1)←(fn(x)+xn−mfm(x),max⁡{In,n+1−In})\left(f_{n+1}(x), I_{n+1}\right) \leftarrow\left(f_{n}(x)+x^{n-m} f_{m}(x), \max \left\{I_{n}, n+1-I_{n}\right\}\right)(fn+1​(x),In+1​)←(fn​(x)+xn−mfm​(x),max{In​,n+1−In​});
3: 若 $n<N-1,n\leftarrow n+1$, 转步骤 2 ;
输出: $\left(f_N(x),I_N\right)$.

容易证明该算法输入的是一个以$\alpha$为输出的联结多项式

定理：(1) $I_N$ 是产生 $\alpha$ 的 LFSR 的最小级数;
(2) 当且仅当 $I_N\le N/2$ 时, 产生 $N$ 长序列 $\alpha$ 的最短 $LFSR$ 是唯 一的;
(3) 当 $I_N<N/2$ 时, 迭代 $2I_N$ 步已经有$\left(f_{2I_N}(x),l_{2I_N}\right)=\left(f_N(x),I_N\right)\text{. }$

Golomb 原则 (1967)：称一个序列是安全的（不容易找到规律的），若：

(1) 周期足够大; (2) 一个周期中统计特性好; (3) 自相关函数是一个二值函数;

计算线性复杂度的其他方法：

定理：设 $a=a_0,a_1,\cdots ,a_{n-1}$ 是 $F_q$ 上的一个 $n$ 长序列, 则$a$的线性复 杂度是下列矩阵的最小秩:
$$A_a=\left(\begin{array}{ccccccc}{a}_0& a_1& a_2& \cdots & a_{n-3}& a_{n-2}& a_{n-1}\\ a_1& a_2& a_3& \cdots & a_{n-2}& a_{n-1}& \ast \\ a_2& a_3& a_4& \cdots & a_{n-1}& \ast & \ast \\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ a_{n-1}& \ast & \ast & \ast & \ast & \ast & \ast \end{array}\right)$$
这里$\ast$代表 $F_q$中的任意元素, 最小秩是指对这些 $\ast$ 的所有可能取值得到的。

定理：设 $a=a_0,a_1,\cdots ,a_{N-1}\cdots$ 是 $F_q$ 上的一个周期为N的序列, 则 $a$ 的线性复杂度是下列矩阵的秩:
$$C_l(a)=\left(\begin{array}{cccc}{a}_0& a_1& \cdots & a_{N-1}\\ a_1& a_2& \cdots & a_0\\ ⋮& ⋮& \cdots & ⋮\\ a_{N-1}& a_0& \cdots & a_{N-2}\end{array}\right)$$

离散傅里叶变换：

设 $(N,q)=1$, 则 存在 $m$ 使得 $F_{q^m}$ 中存在 $N$ 阶元。设 $a^N=a_0,a_1,\cdots ,a_{N-1}$ 是 $F_q$ 上的一个长为 $N$ 的序列, 它的离散傅立叶变换是 $F_{q^m}$ 上的序 列 $A^N=A_0,A_1,\dots ,A_{N-1}$ :
$$\left(A_0,A_1,\cdots ,A_{N-1}\right)=\left(a_0,a_1,\cdots ,a_{N-1}\right)F(\alpha )$$
$$F(\alpha )=\left(\begin{array}{ccccc}1& 1& 1& \cdots & 1\\ 1& \alpha & {\alpha }^2& \cdots & {\alpha }^{N-1}\\ ⋮& ⋮& ⋮& \cdots & ⋮\\ 1& {\alpha }^{N-1}& {\alpha }^{2(N-1)}& \cdots & {\alpha }^{(N-1)(N-1)}\end{array}\right)$$

注意到：$F(\alpha {)}^{-1}=N^{-1}F\left({\alpha }^{-1}\right)$，令：
$$C_r(a)=\left(\begin{array}{cccc}{a}_0& a_1& \cdots & a_{N-1}\\ a_{N-1}& a_0& \cdots & a_{N-2}\\ ⋮& ⋮& \cdots & ⋮\\ a_1& a_2& \cdots & a_0\end{array}\right),D_A=\left(\begin{array}{cccc}{A}_0& & & \\ & A_1& & \\ & & \ddots & \\ & & & A_{N-1}\end{array}\right)$$
则：Blahut定理：

设 $a^{\infty }=a_0,a_1,\cdots ,a_{N-1}\cdots$ 是 $F_q$ 上的一个周期为 $N$ 的序列, 则 $L\left(a^{\infty }\right)=W_H\left(A^N\right),L\left(A^{\infty }\right)=W_H\left(a^N\right)$（$W_H$：非零分量个数）

伪随机数生成器

对于任意的正整数 $n$, 我们设 $U_n$ 是一个取值在 ${\mathbb{Z}}_2^n$ 上的均匀分布 的随机变量, $G$ 是一个确定的多项式时间算法。G称为是一个伪随机数发生器, 如果满足下列两条:

1. 扩展性：当输入$s$长度为$n$时, 输出 $G(s)$ 的长度 $I(n)$ 满足 $I(n)>n$;
2. 伪随机性: 当输入随机变量$U_n$时, 输出随机变量 $G\left(U_n\right)$ 与 $U_{I(n)}$ 不可区分。
   事实上, 任一多项式扩展因子 $I(n)$ 的 PRG 可由扩展因子为 $n+1$ 的 PRG 迭代得到。

Chapter4 RSA公钥密码体制

基础：给定大素数p,q，求n=pq/ 已知n为两个大素数p,q的乘积，求p,q的计算难度完全不同

定义：单向函数：正向求解容易，反向求解困难的函数

限门单向函数：单向函数，但在知道某个秘密参数k后，反向求解容易

基础知识：

Euclid算法：

辗转相除法求a和b的公因数：不妨设a>b，则：

$a=r_0,b=r_1,r_0=q_1{r}_1+r_2,r_1=q_2{r}_2+r_3,...,r_{m-1}=q_m{r}_m+0$，则$gcd(a,b)=r_m$

将满足该组关系的$(r_0,r_1,...,r_m)$的集合看做一个空间，显然其为线性空间，秩为2，一组生成元为：$(r_0=1,r_1=0,r_i=q_{i-1}{r}_{i-1}-r_{i-2}，i=2,...,m)$和$(s_0=0,s_1=1,s_i=q_{i-1}{s}_{i-1}-s_{i-2}，i=2,...,m)$

推论：对任意$(x_0=a,x_1=b)$，其构成的序列$(x_0,x_1,..,x_m)$满足：$\vec{x}=a\vec{r}+b\vec{s}$

若$(a,b)=1$，则$x_m=1$，则$a{r}_m+b{r}_m=1$，则$r_m=a^{-1}(\mathrm{m}\mathrm{o}\mathrm{d}b),s_m=b^{-1}(\mathrm{m}\mathrm{o}\mathrm{d}a)$

记忆：求小的数mod大的数的逆：取$r_0=0,r_1=1$，和辗转相除法同步进行即可，到$x_m=1$时停止

中国剩余定理：

假设整数 $m_1,m_2,\dots ,m_n$ 两两互素, 则对于任意的整数 $a_1,a_2,\dots ,a_n$, 方程组
$$\{\begin{array}{l}x\equiv a_1\left(\mathrm{m}\mathrm{o}\mathrm{d}{m}_1\right)\\ x\equiv a_2\left(\mathrm{m}\mathrm{o}\mathrm{d}{m}_2\right)\\ \cdots \\ x\equiv a_n\left(\mathrm{m}\mathrm{o}\mathrm{d}{m}_n\right)\end{array}$$
都存在整数解, 且若 $X,Y$ 都满足该方程组, 则必有 $X\equiv Y(\mathrm{m}\mathrm{o}\mathrm{d}N)$, 其中 $N={\prod }_{i=1}^n{m}_i$ 。
具体而言, $x\equiv {\sum }_{i=1}^n{a}_i\times \frac{N}{m_i}\times {\left[{\left(\frac{N}{m_i}\right)}^{-1}\right]}_{m_i}(\mathrm{m}\mathrm{o}\mathrm{d}N)$

Lagrange定理：

$(b,n)=1$，则$b^{\phi (n)}=1(\mathrm{m}\mathrm{o}\mathrm{d}n)$

二次剩余：

设p为奇质数，则$|Z_p^{\ast }|=p-1$，$(Z_p^{\ast }{)}^2$为$\frac{p-1}{2}$阶子群，称为mod p的二次剩余（QR§），$Z_p^{\ast }$中的其余元素则称为mod p的非二次剩余。

定义：Legendre符号：$\left(\frac{\alpha }{p}\right)$: =1，若$\alpha$为mod p的二次剩余，=-1，若为非二次剩余，=0，若为0

显然，$\left(\frac{\alpha }{p}\right)$=${\alpha }^{\frac{p-1}{2}}(\mathrm{m}\mathrm{o}\mathrm{d}p)$

扩展：Jacobi符号：定义$\left(\frac{\alpha }{n}\right)=\prod {\left(\frac{\alpha }{p_i}\right)}^{a_i}$

二次互反律：

1. n为奇数：$\left(\frac{2}{n}\right)=\{\begin{array}{rl}1& n=\pm 1mod8\\ -1& else\end{array}$

   记忆方法：找规律

2. n为奇数：$\left(\frac{m_1{m}_2}{n}\right)=\left(\frac{m_1}{n}\right)\left(\frac{m_2}{n}\right)$

3. m,n为奇数：$\left(\frac{m}{n}\right)=\pm \left(\frac{n}{m}\right)\{\begin{array}{rl}-& m\equiv n\equiv -1\mathrm{m}\mathrm{o}\mathrm{d}4\\ +& m\text{ or }n\equiv 1\mathrm{m}\mathrm{o}\mathrm{d}4\end{array}$

   记忆方法：$\left(\frac{m}{n}\right)\left(\frac{n}{m}\right)=(-1{)}^{\frac{n-1}{2}\frac{m-1}{2}}$

mod n的平方根：

p为质数，如果$a\in QR(p)$，则$x^2\equiv a\mathrm{m}\mathrm{o}\mathrm{d}p$恰有两个根$\pm b$

1. 若$p\equiv 3\mathrm{m}\mathrm{o}\mathrm{d}4$，则解为$x\equiv \pm a^{\frac{p+1}{4}}\mathrm{m}\mathrm{o}\mathrm{d}p$
2. 若$n=p^e$，则$x^2\equiv a\mathrm{m}\mathrm{o}\mathrm{d}{p}^e$恰有两解当且仅当$x^2\equiv a\mathrm{m}\mathrm{o}\mathrm{d}p$有解
3. 若$n={\prod }_s{p}_i^{e_i}$，$(a,n)=1$，则$x^2\equiv a\mathrm{m}\mathrm{o}\mathrm{d}n$要么无解，要么有$2^s$个解

RSA体制：

参数设置：p,q为两个约有512位的质数, n=pq, $\phi (n)=(p-1)(q-1)$，取$(e,\phi (n))=1$，求$d\equiv e^{-1}(\mathrm{m}\mathrm{o}\mathrm{d}\phi (n))$，则e和n为公钥，d为私钥，$\phi (n)$为限门

如果只有n，则由于大整数分解的困难性，很难求出$\phi (n)$，故无法求出$d$；但是若有了$\phi (n)$，则进行简单求逆即可求出$d$

加密过程：$m\to m^e$，解密过程：$m\to m^d$，因为$m^{ed}=m$（均为mod n运算）

求解$x^e(\mathrm{m}\mathrm{o}\mathrm{d}n)$的算法：平方乘算法

设e的二进制展开为$(c_m{c}_{m-1}...c_0{)}_2$，则$x^e=x^{c_0}(x^{[c_m..c_1]}{)}^2$，递归即可，至多进行2m+1次乘法运算

脱密计算：

1. 用平方乘算法直接求出$y^d(\mathrm{m}\mathrm{o}\mathrm{d}n)$
2. 分别计算出$y_p\equiv y(\mathrm{m}\mathrm{o}\mathrm{d}p),d_p\equiv d(\mathrm{m}\mathrm{o}\mathrm{d}p-1)，y_q,d_1$，再用中国剩余定理合并两个方程的结果：$x_p\equiv y_p^{d_p}(\mathrm{m}\mathrm{o}\mathrm{d}p)，x_q\equiv y_q^{d_q}(\mathrm{m}\mathrm{o}\mathrm{d}q)$

判断一个数是否为质数的算法：

事实：$\left(\frac{\alpha }{p}\right)$=${\alpha }^{\frac{p-1}{2}}(\mathrm{m}\mathrm{o}\mathrm{d}p)$只对奇数成立，对n为合数至少有一般的$\alpha$不成立

S-S算法：

在1~n-1中随机选取一个数a，令$x=\left(\frac{a}{n}\right)$，若x为0或${\alpha }^{\frac{n-1}{2}}$则返回n为质数，否则返回合数。

这是一个Monte-Carlo算法：如果n为合数则必定返回合数，如果n为质数则有大于1/2的概率为质数

Miller-Rabin算法：

设$n-1=2^{k}m$，其中m为奇数。在1~n-1中随机选取一个数a，令$b=a^m\mathrm{m}\mathrm{o}\mathrm{d}n$，如果$b=1\mathrm{m}\mathrm{o}\mathrm{d}n$，则返回n为质数，否则，

对i=0~k-1，若$b=-1\mathrm{m}\mathrm{o}\mathrm{d}n$，则返回n为质数，否则$b=b^2$

否则，返回n为合数

分析：若n为质数，且返回了n为合数，则要求对i=0~k-1，$b\not\equiv -1\mathrm{m}\mathrm{o}\mathrm{d}n$，但是由于n为质数时完全平方数$x^2=1\mathrm{m}\mathrm{o}\mathrm{d}n$必须$x=\pm 1\mathrm{m}\mathrm{o}\mathrm{d}n$，因此必须$b\equiv 1\mathrm{m}\mathrm{o}\mathrm{d}b=n$，这会返回n为质数，矛盾！故n为质数必定返回质数，同时可以证明n为合数则至少有1/2概率返回合

因子分解算法：

Pollard p-1算法：

n为合数，分解n：只需要寻找一个质因子

算法思想：假设这个质因子-1的各个准质因子都很小

假设$p-1=\prod q_i^{e_i}$，且$q_i^{e_i}\le B$，则$p-1|B!$，$a^{B!}\equiv 1\mathrm{m}\mathrm{o}\mathrm{d}p$，从而$(a^{B!}-1,n)$>1

实际：枚举若干个B即可

Pollard $\rho$算法：

算法思想：构造mod n的同余碰撞：生日悖论：碰撞概率的增加速度远高于单次概率的增长速度

例如，任取23个人则有两个人生日相同的概率已经达到1/2

在$Z_n$中任取k个元素，求$(a_i-a_j,n)$，则碰撞概率为$1/p$，只要搜索1.17$\sqrt{p}$个元素即可

但是两两碰撞的存储空间过大，故改进：

构造函数f，使得$p|a-b\Rightarrow p|f(a)-f(b)$，并且依次迭代比较$f(x_1)$和$f(f(x_2))$，这样在进入{xn=fn(x0)}\{x_n=f^n(x_0)\}{xn​=fn(x0​)}mod p的周期之后必定可以在周期中找到碰撞。

好处：存储空间很小，而且时间复杂度在$\sqrt[4]{n}$