文章目录
二叉树的中序遍历
递归算法
1.代码实现
def inorderTraversal(self, root):
"""
二叉树中序遍历(递归实现)
参数:
root: 二叉树根节点
返回:
List[int]: 中序遍历结果列表
"""
result = []
def inorder(node):
"""递归辅助函数"""
if not node:
return
# 遍历左子树
inorder(node.left)
# 访问根节点
result.append(node.val)
# 遍历右子树
inorder(node.right)
inorder(root)
return result
2. 基本概念
- 中序遍历 :按照"左子树 → 根节点 → 右子树"的顺序访问二叉树节点
- 递归思想 :将问题分解为规模更小的同类问题,直到达到基本情况
3. 算法结构
def inorder(node):
if not node:
return
# 1. 遍历左子树
inorder(node.left)
# 2. 访问根节点
result.append(node.val)
# 3. 遍历右子树
inorder(node.right)
4. 关键要素
4.1 递归终止条件
if not node:
return
- 当节点为空时,直接返回,这是递归的终止条件
- 防止无限递归,确保算法能够正常结束 3.2 递归调用顺序
-
先递归左子树 : inorder(node.left)
- 先处理左子树的所有节点
- 左子树处理完成后,才会执行后续代码
-
访问根节点 : result.append(node.val)
- 将当前节点的值添加到结果列表中
- 这是中序遍历的"中"部分
-
后递归右子树 : inorder(node.right)
- 处理右子树的所有节点
- 这是递归的最后一步
5. 算法特点
5.1 时间复杂度
- O(n) :每个节点只被访问一次,n为节点数量
5.2 空间复杂度
- O(h) :h为二叉树的高度
- 递归调用栈的深度取决于树的高度
- 最坏情况下(树退化为链表),空间复杂度为O(n)
5.3 递归调用栈
- 每次递归调用都会在调用栈中创建一个新的栈帧
- 栈帧中保存了当前节点的信息和返回地址
- 递归返回时,从栈帧中恢复执行状态
6. 递归与迭代的对比
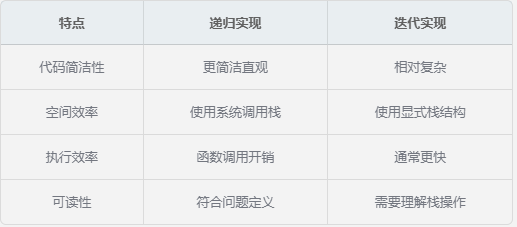
递归实现直接对应中序遍历的定义,代码简洁明了,但可能会因为递归深度过大导致栈溢出。在实际应用中,对于深度较大的树,可以考虑使用迭代实现。
7.实例演示递归序
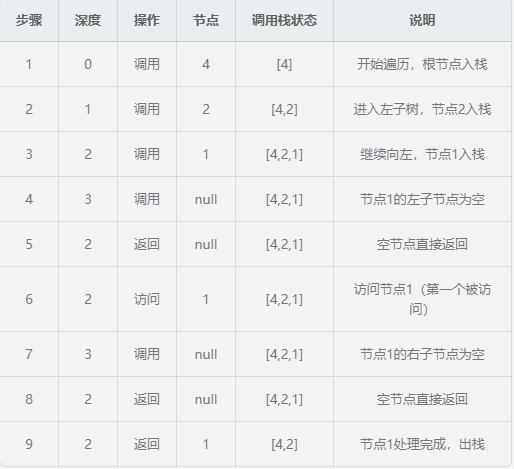
用文字和表格展示完全二叉树 [4, 2, 6, 1, 3, 5, 7] 的递归序完整周期。
4
/ \
2 6
/ \ / \
1 3 5 7
7.1递归序完整周期分析
第一阶段:递归进入(沿左子树向下)
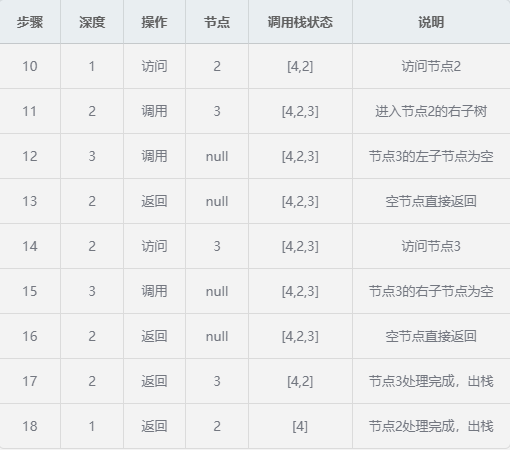
第二阶段:处理节点2及其右子树
第三阶段:处理根节点4及其右子树
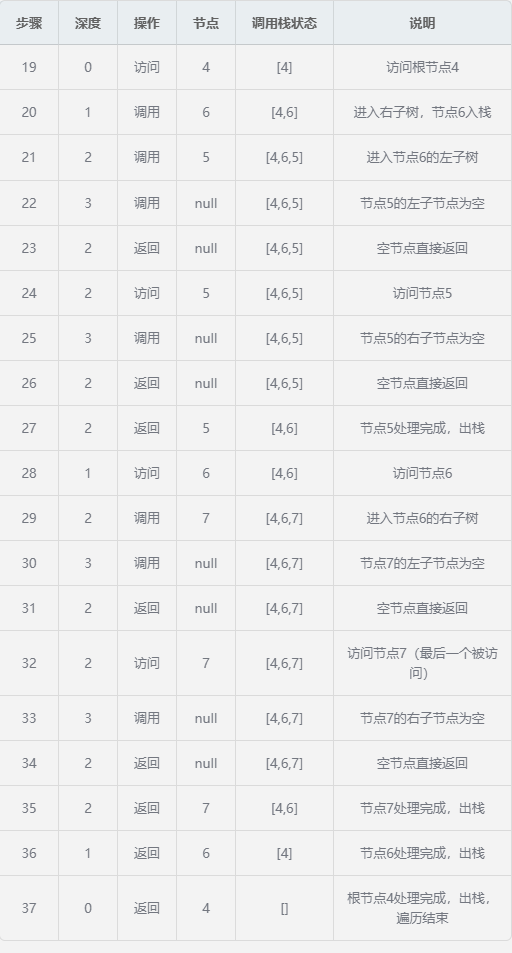
7.2关键观察
- 节点访问顺序 :1 → 2 → 3 → 4 → 5 → 6 → 7(中序遍历结果)
- 最大递归深度 :3(树的高度)
- 最大栈大小 :3(节点4、2、1同时在栈中)
- 每个节点的处理模式 :
- 调用(入栈)
- 访问(处理节点值)
- 返回(出栈)
- 递归序特点 :
- 先沿左子树一直向下到最深处
- 然后按"左-根-右"顺序访问节点
- 最后逐层返回
7.3总结
这个完整周期展示了递归中序遍历的三个关键阶段:
- 递归进入 :从根节点开始,沿左子树一直向下
- 节点处理 :按中序顺序访问节点(左-根-右)
- 递归退出 :处理完节点后逐层返回
通过这个表格,我们可以清晰地看到递归调用栈的动态变化,以及每个节点在何时被调用、访问和返回。
迭代算法
1.代码实现
def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
""" # 修正:缩进与函数内部代码一致(4个空格)
二叉树中序遍历(迭代实现)
参数:
root: 二叉树根节点
返回:
List[int]: 中序遍历结果列表
"""
result = [] # 缩进与文档字符串对齐,属于函数内部代码块
stack = []
current = root
# 使用栈模拟递归过程:先遍历所有左子节点,再访问根节点,最后遍历右子节点
while current or stack:
# 1. 将当前节点及其所有左子节点入栈(先处理左)
while current:
stack.append(current)
current = current.left
# 2. 弹出栈顶节点,加入结果列表(处理中)
current = stack.pop()
result.append(current.val)
# 3. 转向右子节点(处理右)
current = current.right
return result
2.算法原理
迭代实现使用 栈 来模拟递归过程,避免了递归调用带来的系统开销。中序遍历的顺序是"左-根-右",迭代实现的关键是:
- 先访问最左边的节点 :通过不断向左移动并将节点入栈
- 访问栈顶节点 :当到达最左边时,弹出栈顶节点并访问
- 转向右子树 :访问完当前节点后,转向其右子树继续遍历
3.执行步骤详解
以二叉树 [4, 2, 6, 1, 3, 5, 7] 为例:
4
/ \
2 6
/ \ / \
1 3 5 7
初始状态
- result = []
- stack = []
- current = root(4) 执行过程
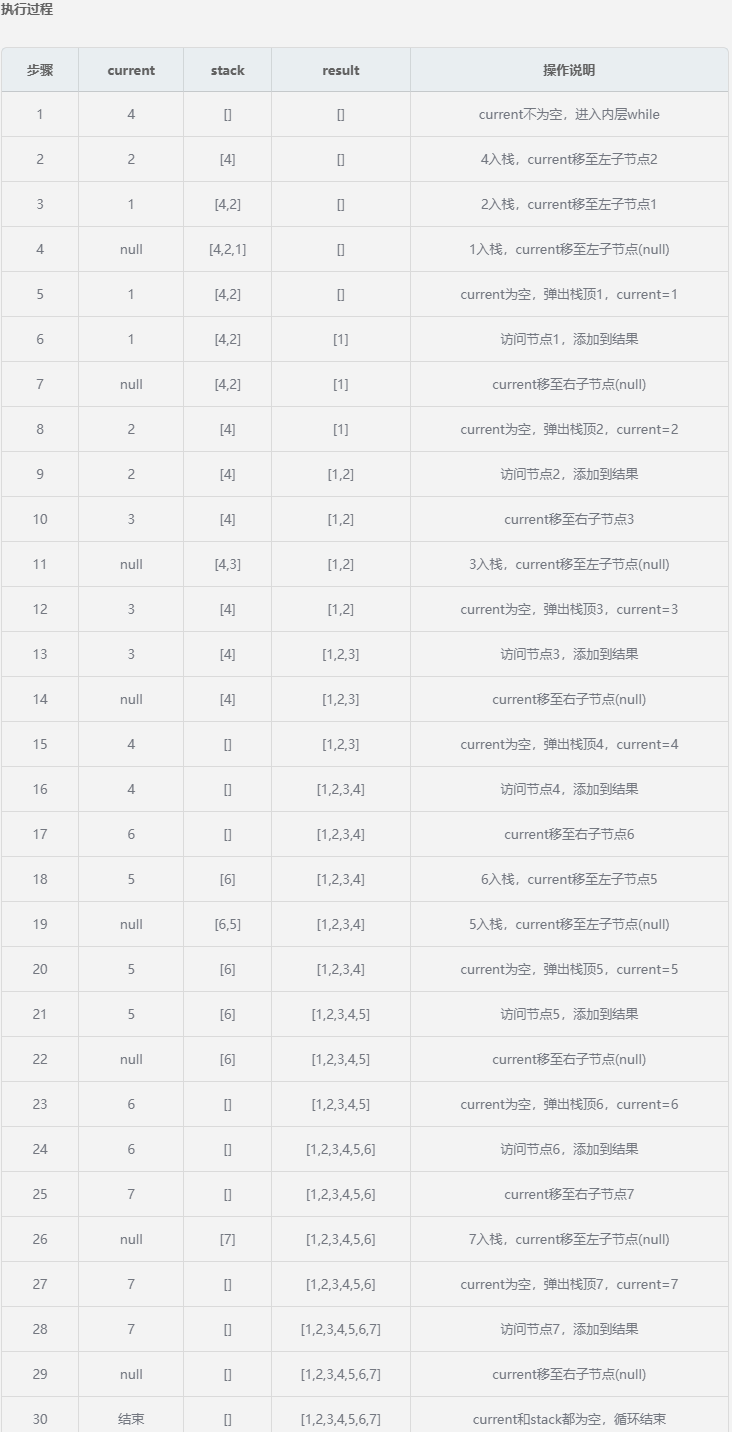
4.关键点解析
- 外层循环条件 : while current or stack
- 只要当前节点不为空或栈不为空,就继续遍历
- 这确保了所有节点都能被访问到
- 内层循环 : while current
- 将当前节点及其所有左子节点入栈
- 直到到达最左边的叶子节点
- 节点访问 :
- 弹出栈顶节点(最左边的未访问节点)
- 访问该节点(将其值加入结果列表)
- 转向其右子树继续遍历
5.优势与适用场景
- 优势 :
- 避免了递归深度过大导致的栈溢出
- 没有函数调用的额外开销
- 可以更好地控制内存使用
- 适用场景 :
- 树的深度可能很大,递归可能导致栈溢出
- 对性能要求较高的场景
- 需要精确控制内存使用的环境
这种迭代实现是二叉树遍历的经典算法,通过栈结构巧妙地模拟了递归过程,实现了与递归相同的效果,但避免了递归的潜在问题。
递归实现 vs 迭代实现的核心区别
递归实现中的栈操作时机
在递归实现中:
- 调用(入栈) :执行 inorder(node) 时立即入栈
- 访问节点 :执行 result.append(node.val) 时,节点 仍然在栈中
- 返回(出栈) :整个函数执行完毕(包括左子树、访问节点、右子树)后才出栈
因此,在递归序的步骤6中: - 操作类型是 访问 节点1
- 此时节点1 尚未返回 ,所以仍然在调用栈中
- 调用栈状态保持为 [4,2,1]
- 直到步骤9执行 返回 操作时,节点1才会出栈,栈状态变为 [4,2]
迭代实现中的栈操作时机
在迭代实现中:
- 入栈 :主动将节点压入栈中
- 出栈 :当需要访问节点时,先将节点弹出栈
- 访问节点 :在弹出栈之后执行
所以在迭代实现中,访问节点1的步骤会同时执行出栈操作,栈状态会立即变化。
为什么会有这种差异?
这是因为:
- 递归实现 :调用栈由系统自动管理,函数执行过程中节点始终在栈中,直到完全执行完毕
- 递归序 :描述的是递归函数的逻辑执行顺序,区分了"访问节点"和"返回"两个不同阶段
- 迭代实现 :我们手动管理栈,需要将"出栈"和"访问"合并为一个操作步骤
二叉树的前序遍历
递归代码实现
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
"""
二叉树的前序遍历
:param root: 二叉树的根节点
:return: 前序遍历的节点值列表
"""
# 方法一:递归实现
result = []
def traverse(node):
if not node:
return
# 前序遍历:根节点 -> 左子树 -> 右子树
result.append(node.val)
traverse(node.left)
traverse(node.right)
traverse(root)
return result
迭代代码实现
def preorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
"""
二叉树的前序遍历
:param root: 二叉树的根节点
:return: 前序遍历的节点值列表
"""
# 方法二:迭代实现
if not root:
return []
result = []
stack = [root] # 使用栈来模拟递归过程
while stack:
node = stack.pop() # 弹出栈顶节点
result.append(node.val) # 访问根节点
# 注意:栈是先进后出,所以先压入右子节点,再压入左子节点
# 这样弹出时会先处理左子节点,符合前序遍历顺序
if node.right:
stack.append(node.right)
if node.left:
stack.append(node.left)
return result
二叉树的后序遍历
递归代码实现
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
"""
二叉树的后序遍历
:param root: 二叉树的根节点
:return: 后序遍历的节点值列表
"""
# 方法一:递归实现
result = []
def traverse(node):
if not node:
return
# 后序遍历:左子树 -> 右子树 -> 根节点
traverse(node.left)
traverse(node.right)
result.append(node.val)
traverse(root)
return result
迭代代码实现
def postorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
"""
二叉树的后序遍历
:param root: 二叉树的根节点
:return: 后序遍历的节点值列表
"""
# 方法二:迭代实现
"""
迭代实现后序遍历的核心思想:
1. 使用栈来模拟递归过程
2. 后序遍历顺序:左子树 -> 右子树 -> 根节点
3. 技巧:先按照根节点 -> 右子树 -> 左子树的顺序遍历,然后反转结果
4. 这样可以复用前序遍历的思路,只是调整子节点的入栈顺序
"""
if not root:
return []
result = []
stack = [root] # 初始化栈,将根节点压入栈中开始遍历
while stack: # 栈不为空时继续遍历
node = stack.pop() # 弹出栈顶节点
result.append(node.val) # 访问根节点
# 注意:栈是先进后出,我们希望最终结果是左子树 -> 右子树 -> 根节点
# 所以先压入左子节点,再压入右子节点
# 这样弹出时会先处理右子节点,得到根->右->左的顺序
if node.left: # 如果有左子节点,先压入栈
stack.append(node.left)
if node.right: # 如果有右子节点,后压入栈
stack.append(node.right)
# 反转结果得到后序遍历顺序:左 -> 右 -> 根
return result[::-1]






















 631
631

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










