前/中/后缀表达式的转换
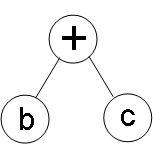

自然表达式转换为前/中/后缀表达式,其实是很简单的。首先将自然表达式按照优先级顺序,构造出与表达式相对应的二叉
树,然后对二叉树进行前/中/后缀遍历,即得到前/中/后缀表达式。
举例说明将自然表达式转换成二叉树:
a×(b+c)-d
① 根据表达式的优先级顺序,首先计算(b+c),形成二叉树

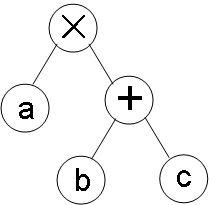
②然后是a×(b+c),在写时注意左右的位置关系

③最后在右边加上 -d

然后最这个构造好的二叉树进行遍历,三种遍历的顺序分别是这样的:
① 前序遍历:根-左-右
② 中序遍历:左-根-右
③ 后序遍历:左-右-根
所以还是以刚才的这个例子,在最终二叉树的基础上可以得出:
前缀表达式:-*a+bcd
中缀表达式:a*b+c-d
后缀表达式:abc+*d-




 本文详细介绍了如何将自然表达式转换为前缀、中缀和后缀表达式,通过构建对应的二叉树并进行不同类型的遍历来实现转换。
本文详细介绍了如何将自然表达式转换为前缀、中缀和后缀表达式,通过构建对应的二叉树并进行不同类型的遍历来实现转换。

















 1429
1429

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










